2. 程式人生 > >市場研究中的資料分析知識整理 （九）-聯合分析

市場研究中的資料分析知識整理 （九）-聯合分析

阿新 • • 發佈：2019-01-02

聯合分析

聯合分析所要解決的是，在研究的產品或服務中，具有哪些特徵的產品最能得到消費者的歡迎。一件產品通常擁有許多特徵如價格、顏色、款式以及產品的特有功能等，那麼在這些特性之中，每個特性對消費者的重要程度如何？在同樣的（機會）成本下，產品具有哪些特性最能贏得消費者的滿意？

基於度量的聯合分析

基於度量的聯合分析將會涉及多層次的迴歸巢狀的問題，分層線性模型將能有效的解決這一問題。
分層模型假設每個受訪者有一組偏好係數，這些係數來自更大的分佈，而這個更大分佈決定了個體可能的偏好值。

基於度量的聯合分析的分層線性模型要解決：

  • 基於使用者對於產品不同特徵的評分，獲得每個特徵對總評分的貢獻。
  • 使用HLM來估計使用者對於產品總體固定的效應和個體水平隨機的效應。

cja_1 <- read.csv("http://r-marketing.r-forge.r-project.org/data/rintro-chapter9conjoint.csv")
cja_1$speed <- factor(cja_1$speed)
cja_1$height <- factor(cja_1$height)
summary(cja_1)

   resp.id           rating       speed     height       const         theme
 
     
 Min.   :  1.00   Min.   : 1.000   40: 800   200:1400   Steel:1400   Dragon:1600  
 1st Qu.: 50.75   1st Qu.: 3.000   50:1200   300:1200   Wood :1800   Eagle :1600  
 Median :100.50   Median : 5.000   60: 800   400: 600                             
 Mean   :100.50   Mean   : 5.268   70: 400                                        
 3rd Qu.:150.25
 
   3rd Qu.: 7.000                                                  
 Max.   :200.00   Max.   :10.000

可以看出，資料由四個特徵變數對於一個評分範圍為1~10的水平變數。

特徵貢獻模型

cja_lm <- lm(rating ~ speed + height + const + theme, data = cja_1)
summary(cja_lm)

結果輸出：

Call:
lm(formula = rating ~ speed + height + const + theme, data = cja_1)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.8394 -1.3412 -0.0186  1.2798  6.9269 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.07307    0.08102  37.932  < 2e-16 ***
speed50      0.82077    0.10922   7.515 7.35e-14 ***
speed60      1.57443    0.12774  12.326  < 2e-16 ***
speed70      4.48697    0.15087  29.740  < 2e-16 ***
height300    2.94551    0.09077  32.452  < 2e-16 ***
height400    1.44738    0.12759  11.344  < 2e-16 ***
constWood   -0.11826    0.11191  -1.057    0.291    
themeEagle  -0.75454    0.11186  -6.745 1.81e-11 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.967 on 3192 degrees of freedom
Multiple R-squared:  0.5039,    Adjusted R-squared:  0.5029 
F-statistic: 463.2 on 7 and 3192 DF,  p-value: < 2.2e-16

通過特徵貢獻模型可知，截距（包含了未顯示的constSteel和themeDragon）+ speed70 +height300的組合的評分是最高的。
但這一模型只是解決了總體性的偏好水平，但並不意味著大部分人喜歡這一組合,cja_lm模型僅有固定效應，這就需要分層線性模型來解決總體平均偏好和組內個體偏好。

截距分層線性模型

library(lme4)
#「(1 | resp.id)」是hlm()中指定隨機效應變數的方式，其中「1」代表截距，「|」是指定符，「resp.id」則表示該模型希望看到個體層面的效應，其標準表示式為「(predictor | group)」。
cja_hlm1 <- lmer(rating ~ speed + height + const + theme + (1 | resp.id), data = cja_1)
summary(cja_hlm1)

結果輸出：

Linear mixed model fit by REML ['lmerMod']
Formula: rating ~ speed + height + const + theme + (1 | resp.id)
   Data: cja_1

REML criterion at convergence: 13324.2

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.3970 -0.6963  0.0006  0.6700  3.3689 

Random effects:
 Groups   Name        Variance Std.Dev.
 resp.id  (Intercept) 0.3352   0.5789  
 Residual             3.5358   1.8804  
Number of obs: 3200, groups:  resp.id, 200

Fixed effects:
            Estimate Std. Error t value
(Intercept)  3.07307    0.08759   35.08
speed50      0.82077    0.10439    7.86
speed60      1.57443    0.12209   12.90
speed70      4.48697    0.14421   31.11
height300    2.94551    0.08676   33.95
height400    1.44738    0.12195   11.87
constWood   -0.11826    0.10696   -1.11
themeEagle  -0.75454    0.10692   -7.06

Correlation of Fixed Effects:
           (Intr) sped50 sped60 sped70 hgh300 hgh400 cnstWd
speed50    -0.329                                          
speed60    -0.144  0.646                                   
speed70    -0.088  0.482  0.602                            
height300  -0.374 -0.311 -0.466 -0.381                     
height400  -0.166 -0.529 -0.412 -0.174  0.428              
constWood  -0.191 -0.437 -0.370 -0.278  0.234  0.547       
themeEagle -0.178  0.183 -0.136 -0.270  0.181 -0.351 -0.563

輸出結果解讀：

  • 固定效應（Fixed effects）部分（模型總體水平）與lm模型一致；
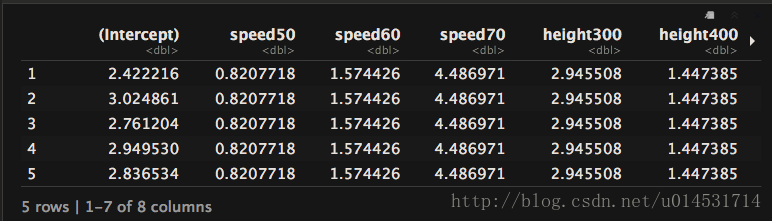
fixef(cja_hlm1)
(Intercept)     speed50     speed60     speed70   height300   height400   constWood  themeEagle 
  3.0730724   0.8207718   1.5744257   4.4869715   2.9455084   1.4473848  -0.1182553  -0.7545428
  • 隨機效應（Random effects）顯示從200個受訪者中獲得了3200個觀測，可通過ranef()獲得單個個體的截距項隨機效應;
ranef(cja_hlm1)$resp.id[1:5,]
(Intercept)
<dbl>
1   -0.65085636         
2   -0.04821158         
3   -0.31186867         
4   -0.12354218         
5   -0.23653807
  • 個體對應的整體固定效應（適用於每個個體的）和個體隨機效應（截距項）可用coef()獲得，個體水平的截距項是由固定效應+個體隨機效應構成，如3號客戶截距項= 3.07fixed - 0.31raned = 2.76coef
coef(cja_hlm1)$resp.id[1:5,]

這裡寫圖片描述

係數分層線性模型

library(lme4)
#繼續使用「(predictor | group)」便可獲得個體層面係數的分層線性模型。通過「control」來設定最高迭代次數（maxfun）。對於迭代收斂情況，如果max>=0.01，可以2、5、10增加迭代次數。
cja_hlm2 <- lmer(rating ~ speed + height + const + theme + 
                   (speed + height + const + theme | resp.id), data = cja_1,
                 control = lmerControl(optCtrl = list(maxfun = 20000)))

對於模型結果，可隨即抽取任意（121號）客戶的係數水平檢視：

coef(cja_hlm2)$resp.id[121,]

這裡寫圖片描述

基於選擇的聯合分析

基於選擇的聯合分析所要面對的資料結構與基於度量的聯合分析不同，前者將不同的產品屬性組合為不同選項，問卷物件則直接選擇相應的屬性組合，模型需要展示不同產品特徵和消費者在不同產品特徵中選擇狀況的關係。
對此，多類別logit選擇模型可用來解決這一問題。

基於選擇的聯合分析要解決：

  • 不同產品特徵集合中，使用者的選擇份額預測；
  • 報告模型的份額估計，即每個產品特徵對應的購買意願。

資料匯入與說明

該資料為一份模擬汽車購買意向的問卷調查資料，對於產品的特徵的描述被組合為3個選項。
這裡寫圖片描述


cja_2 <- read.csv("http://r-marketing.r-forge.r-project.org/data/rintro-chapter13conjoint.csv", colClasses = c(seat ="factor", price = "factor"))
summary(cja_2)

    resp.id            ques         alt    carpool    seat     cargo     
 Min.   :  1.00   Min.   : 1   Min.   :1   no :6345   6:3024   2ft:4501  
 1st Qu.: 50.75   1st Qu.: 4   1st Qu.:1   yes:2655   7:2993   3ft:4499  
 Median :100.50   Median : 8   Median :2              8:2983             
 Mean   :100.50   Mean   : 8   Mean   :2                                 
 3rd Qu.:150.25   3rd Qu.:12   3rd Qu.:3                                 
 Max.   :200.00   Max.   :15   Max.   :3                                 
   eng       price         choice      
 elec:3010   30:2998   Min.   :0.0000  
 gas :3005   35:2997   1st Qu.:0.0000  
 hyb :2985   40:3005   Median :0.0000  
                       Mean   :0.3333  
                       3rd Qu.:1.0000  
                       Max.   :1.0000

此外，對於這類選擇問題，可使用xtabs()檢視其對應屬性的選擇頻數。

xtabs(choice ~seat,data = cja_2)
seat
   6    7    8 
1164  854  982

擬合併對比選擇模型

#mlogit模型需要對應的資料格式
library(mlogit)
#選擇模型的資料結構生成函式中，choice對應原則與否的判斷，shape表明資料框的樣式（「long」和「wide」兩種形式，），varying則指示出選擇項是哪些，alt.levels則是不同問題下的值名稱，id.var則指示出使用者ID項。
cja_2_ml <- mlogit.data(cja_2, choice = "choice",shape = "long", varying = 3:6, alt.levels = paste("pos",1:3), id.var = "resp.id")

#第一個模型是沒有截距（以「0」表示）
cja_ml1 <- mlogit(choice ~ 0 + seat + cargo + eng + price, data = cja_2_ml)
summary(cja_ml1)

#第二個模型則考慮截距存在的模型，該模型中的截距是問題出現在的位置
cja_ml2 <- mlogit(choice ~ seat + cargo + eng + price, data = cja_2_ml)
summary(cja_ml2)

#第三個模型則是將價格轉變為數值變數
cja_ml3 <- mlogit(choice ~ 0 + seat + cargo + eng + as.numeric(as.character(price)), data = cja_2_ml)
summary(cja_ml3)

輸出結果：

Call:
mlogit(formula = choice ~ 0 + seat + cargo + eng + price, data = cja_2_ml, 
    method = "nr", print.level = 0)

Frequencies of alternatives:
  pos 1   pos 2   pos 3 
0.32700 0.33467 0.33833 

nr method
5 iterations, 0h:0m:0s 
g'(-H)^-1g = 7.84E-05 
successive function values within tolerance limits 

Coefficients :
          Estimate Std. Error  t-value  Pr(>|t|)    
seat7    -0.535280   0.062360  -8.5837 < 2.2e-16 ***
seat8    -0.305840   0.061129  -5.0032 5.638e-07 ***
cargo3ft  0.477449   0.050888   9.3824 < 2.2e-16 ***
enggas    1.530762   0.067456  22.6926 < 2.2e-16 ***
enghyb    0.719479   0.065529  10.9796 < 2.2e-16 ***
price35  -0.913656   0.060601 -15.0765 < 2.2e-16 ***
price40  -1.725851   0.069631 -24.7856 < 2.2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log-Likelihood: -2581.6

Call:
mlogit(formula = choice ~ seat + cargo + eng + price, data = cja_2_ml, 
    method = "nr", print.level = 0)

Frequencies of alternatives:
  pos 1   pos 2   pos 3 
0.32700 0.33467 0.33833 

nr method
5 iterations, 0h:0m:0s 
g'(-H)^-1g = 7.86E-05 
successive function values within tolerance limits 

Coefficients :
                   Estimate Std. Error  t-value  Pr(>|t|)    
pos 2:(intercept)  0.028980   0.051277   0.5652    0.5720    
pos 3:(intercept)  0.041271   0.051384   0.8032    0.4219    
seat7             -0.535369   0.062369  -8.5840 < 2.2e-16 ***
seat8             -0.304369   0.061164  -4.9763 6.481e-07 ***
cargo3ft           0.477705   0.050899   9.3854 < 2.2e-16 ***
enggas             1.529423   0.067471  22.6677 < 2.2e-16 ***
enghyb             0.717929   0.065554  10.9517 < 2.2e-16 ***
price35           -0.913777   0.060608 -15.0769 < 2.2e-16 ***
price40           -1.726878   0.069654 -24.7922 < 2.2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log-Likelihood: -2581.3
McFadden R^2:  0.21674 
Likelihood ratio test : chisq = 1428.5 (p.value = < 2.22e-16)

Call:
mlogit(formula = choice ~ 0 + seat + cargo + eng + as.numeric(as.character(price)), 
    data = cja_2_ml, method = "nr", print.level = 0)

Frequencies of alternatives:
  pos 1   pos 2   pos 3 
0.32700 0.33467 0.33833 

nr method
5 iterations, 0h:0m:0s 
g'(-H)^-1g = 8E-05 
successive function values within tolerance limits 

Coefficients :
                                  Estimate Std. Error  t-value  Pr(>|t|)    
seat7                           -0.5345392  0.0623518  -8.5730 < 2.2e-16 ***
seat8                           -0.3061074  0.0611184  -5.0084 5.488e-07 ***
cargo3ft                         0.4766936  0.0508632   9.3721 < 2.2e-16 ***
enggas                           1.5291247  0.0673982  22.6879 < 2.2e-16 ***
enghyb                           0.7183908  0.0654963  10.9684 < 2.2e-16 ***
as.numeric(as.character(price)) -0.1733053  0.0069398 -24.9726 < 2.2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Log-Likelihood: -2582.1

通過lrtest()對比模型差異，可以發現三個模型沒有顯著差異。同時，基於引數最簡原則，選擇第三個模型繼續分析。

lrtest(cja_ml1,cja_ml2,cja_ml3)
Likelihood ratio test

Model 1: choice ~ 0 + seat + cargo + eng + price
Model 2: choice ~ seat + cargo + eng + price
Model 3: choice ~ 0 + seat + cargo + eng + as.numeric(as.character(price))
  #Df  LogLik Df  Chisq Pr(>Chisq)
1   7 -2581.6                     
2   9 -2581.3  2 0.6789     0.7122
3   6 -2582.1 -3 1.5843     0.6630

模型解讀

選擇模型輸出的係數結果並不顯見，為了解決最開始提出的問題，需要進一步處理。

單一屬性的支付意願
#價格是以million為單位，需要換算為「萬」
coef(cja_ml3)["enghyb"]/((-coef(cja_ml3))["as.numeric(as.character(price))"]/1000)

  enghyb 
4145.234

此處的支付意願是說，當兩類車（混動和汽油）的平均價格差距大於4145.234刀左右，則消費者對二者沒有明顯偏好，選擇混動和汽油的使用者數量是接近的。

選擇份額模擬

本部分解決產品設計的不同屬性如何影響使用者選擇的份額的。

#準備待預測的資料
#列出所有可能
attrb <- list(seat = c("6", "7", "8"),
                cargo = c("2ft", "3ft"),
                eng = c("gas", "hyb", "elec"),
                price = c("30", "35", "40"))
#從中任意選取幾類，以便進行模擬預測
neu_df <- expand.grid(attrb)[c(1,4,9,12,42),]
neu_df
prdct_mlt <- function(mdl,df){
  #將以因子形式儲存的資料轉化為數值矩陣，其中update()是將模型公式中的右邊部分作為輸入項，因為沒有截距的緣故，需要「[,-1]」刪除第一列
  data.model <- model.matrix(update(mdl$formula, 0 ~ .),data = df)[,-1]
  #將編碼後的資料和模型中的係數矩陣相乘「%*%」，從而集合各個不同屬性產品的不同效用值
  utility <- data.model%*% mdl$coef

  share <- exp(utility)/sum(exp(utility))
  cbind(share,df)
}
prdct_mlt(cja_ml3,neu_df)

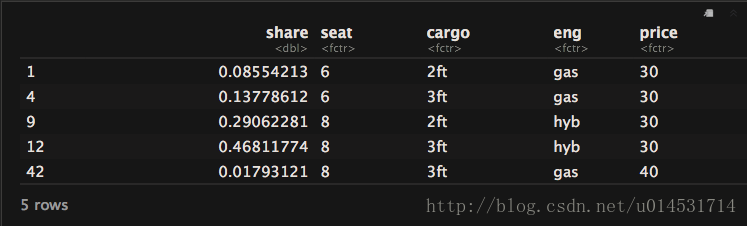
這裡寫圖片描述
解讀：若是使用模擬的產品組合來問消費者，則有可能有超過四成使用者選擇12號方案。同時，對於差異很小或等價的不同設計方案之間的預測份額不合理情況存在「紅藍公交問題」，需要注意避免。

相關推薦

市場研究中的資料分析知識整理 （九）-聯合分析

聯合分析 聯合分析所要解決的是，在研究的產品或服務中，具有哪些特徵的產品最能得到消費者的歡迎。一件產品通常擁有許多特徵如價格、顏色、款式以及產品的特有功能等，那麼在這些特性之中，每個特性對消費者的重要程度如何？在同樣的（機會）成本下，產品具有哪些特性最能

Java基礎知識複習（九） -- 刪除ArrayList中的資料

首先初始化一個Hero集合，裡面放100個String物件，名稱分別是從 str 0 str 1 str 2 … str 99. 通過遍歷的手段，刪除掉名字編號是8的倍數的物件 若最簡單的使用位置查詢的方式來刪除對應物件會發現，若每次查詢並刪除，後面的物件會自動前移

大資料系列之Hadoop知識整理（七）MapReduce的核心之Shuffle詳解

1.MapReduce的核心之shuffle詳解 上一篇中我們介紹了MapReduce是什麼，以及MapReduce的執行過程，其中在執行過程中主要分為Map端與Reducer端，MapReduce計算模型主要完成了對映與化簡，在這其中，有一個最重要的過程那就是其核心——s

大資料系列之資料倉庫Hive知識整理（四）Hive的嚴格模式，動態分割槽，排序，事務，調優

1.Hive的嚴格模式Hive提供了一個嚴格模式，可以防止使用者執行那些產生意想不到的不好的影響的查詢。想想看在那麼大的資料量的前提下，如果我們在分割槽上表上使用查詢所有，或是使用了笛卡爾積查詢資料等等不良情況，那得花費我們多少時間和資源成本，Hive在預設情況下會開啟一種模

大資料系列之資料庫Hbase知識整理（一）Hbase簡介，叢集搭建

1.Hbase簡介   HBase是一個分散式的、面向列的開源資料庫，該技術來源於 Fay Chang 所撰寫的Google論文“Bigtable：一個結構化資料的分散式儲存系統”。就像Bigtable利用了Google檔案系統（File System）所提供的分散式資料儲

Java基礎知識整理（一）

顯式 sys 轉換 強制 print pri 字符 parse ger Java開發環境JDK(Java編輯器、Java運行工具（JRE作用）、Java文檔生成工具、Java打包工具) 1.Java是嚴格區分大小寫的。2.Java程序中一句連續的字符串不能分開在兩行書寫，

《HTML5與CSS3權威指南》知識整理（1）

scrip 自動驗證 視頻 err ide p s sil html5 oca 《HTML5與CSS3權威指南》知識點整理（1） 1、新增標簽 新增語義化標簽。 <header> 定義 section 或 page 的頁眉。 <nav>定義

ES6知識整理（6）--Symbol函數

edi sans tap BE undefine tle cti type 很多 （文章會同步到博客園，技術類文章還是該讓搜索引擎察覺比較好）symbol是js的第7種數據類型：7種分別是：undefined、null、boolean（布爾）、string（字符串）、num

ES6知識整理（7）--Set和Map數據結構

ora ear 踏實 9.png 叠代 數據 edi KS 返回鍵 （文章會同步到博客園，技術類文章還是該讓搜索引擎察覺比較好）Set構造函數初始化一個值不重復的數組，適合做數組去重。2種數組去重的方法：這裏再說下Array.from()，表示以一個類數組||可叠代對象，創

MySQL知識整理（一）

   MySQL基礎知識   資料庫相關概念 DB：database，即是資料庫，裡面儲存了有組織的規範資料。 DBMS：database management system，即是資料庫管理系統，簡稱資料庫軟體、資料庫產品，資料庫是通過DBMS建立和

Spring5知識整理（二）

Spring的表示式語言spEL Spring表示式語言（SpEL）：是一個支援執行時查詢和操作物件圖的強大表示是語言,是一種可以與一個基於spring的應用程式中的執行時物件互動的東西。總得來說SpEL表示式是一種簡化開發的表示式，通過使用表示式來簡化開發，減少一些邏輯、配置的編寫。

java基礎知識整理（1）

一、學習的前提          (1)目標要明確          (2)興趣是最好的老師    

java基礎知識整理（7）——繼承與抽象

一、繼承 1、概述          多個類中存在相同屬性和行為時，將這些相同的內容抽取到單獨一個類中，那麼多個類無需再定義這些屬性和行為，只要繼那個類即可。多個類可以稱為子類，單獨這個類稱為父類或者超類。子類可

大資料基礎知識集合（三）

一、Hadoop 1、MapReduce——Hadoop的核心 MapReduce是一個可以對大量資料進行分散式處理的軟體框架，MapReduce的重要創新是當處理一個大資料集查詢時會將其任務分解並在執行的多個節點中處理。 當資料量很大時就無法在一臺伺服器上解決問題，此時分

深度學習/機器學習入門基礎數學知識整理（一）：線性代數基礎，矩陣，範數等

前面大概有2年時間，利用業餘時間斷斷續續寫了一個機器學習方法系列，和深度學習方法系列，還有一個三十分鐘理解系列（一些趣味知識）；新的一年開始了，今年給自己定的學習目標——以補齊基礎理論為重點，研究一些基礎課題；同時逐步繼續寫上述三個系列的文章。 最近越來越多的

劍指offer演算法題分析與整理（一）

下面整理一下我在刷劍指offer時，自己做的和網上大神做的各種思路與答案，自己的程式碼是思路一，保證可以通過，網友的程式碼提供出處連結。 目錄 1、陣列中的逆序對 在陣列中的兩個數字，如果前面一個數字大於後面的數字，則這兩個數字組成一個逆序對。輸

深度學習/機器學習入門基礎數學知識整理（五）：Jensen不等式簡單理解，共軛函式

Jensen不等式及其延伸 凸函式最基本的不等式性質，又稱Jensen不等式[1] f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y) 通俗一點講就是，期望的函式值小於等於函式值的期望。

DataMining學習1_資料探勘技術（三）——關聯分析

3、關聯分析 3.1、基本概念  （1）通常認為項在事物中出現比不出現更重要，因此項是非對稱二元變數。（2）關聯規則是形如X->Y的蘊涵表示式，其中X和Y是不相交的項集，即X交Y=空。（3）由關聯規則作出的推論並不必然蘊涵因果關係。它只表示規則前件和後件中的項明

資料分析學習筆記（七）-- 股價分析

本例子，通過numpy分析股價 csv檔案讀寫 CSV（Comma-Separated Value，逗號分隔值）是一種常見的檔案格式，通常資料庫的轉存檔案就是csv格式，檔案中的各個欄位對應於資料庫表中的列。 這裡有一份csv格式的檔案，本文一該檔案資

機器學習中常見的問題整理（二）

1.KNN演算法有哪些缺點？ （1）計算代價很大 ①由於KNN必須對分類資料計算與每一個訓練資料的距離，非常耗時； ②KNN演算法必須儲存全部的資料集，如果訓練資料集很大，那麼就需要耗費大量的儲存空間； （2）無法處理categorical變數