十三、神經網路梯度不穩定問題(即梯度消失 & 梯度爆炸問題)
本部落格主要內容為圖書《神經網路與深度學習》和National Taiwan University (NTU)林軒田老師的《Machine Learning》的學習筆記,因此在全文中對它們多次引用。初出茅廬,學藝不精,有不足之處還望大家不吝賜教。
歡迎大家在評論區多多留言互動~~~~
1 . 梯度不穩定的淺層分析
眾所周知,使用深層次的神經網路往往會獲得比淺層次神經網路更為優秀的效果。但是深度神經網路的訓練也是是跟令人頭疼的,因為一個深度神經網路train不好的話很有可能在效果上與只含有一個隱層的神經網路的效果相差甚遠。在這裡我們就要分析一下神經網路難以訓練的原因。
造成這種現象的和主要原因在於在深度網路中,不同的層學習的速度差異很大。尤其是,在網路中後面的層學習的情況很好的時候,先前的層次常常會在訓練時停滯不變,基本上學不到東西,這種停滯稱為梯度消失問題(vanishing gradient problem)。這種停滯並不是因為運氣不好。而是,有著更加根本的原因使學習的速度下降了,這些原因和基於梯度的學習技術相關。
在前面的層中的梯度會變得非常大,這也叫做梯度爆炸問題 ( exploding gradient problem),這也沒比梯度消失問題更好處理。更加一般地說,在深度神經網路中的梯度是不穩定的,在前面的層中或會消失,或會激增。這種不穩定性才是深度神經網路中基於梯度學習的根本問題。
2 . 梯度不穩定的原理性分析
假設在神經網路中使用的是 sigmoid 神經元,我們可以得到 sigmoid 導數的函式影象如下所示
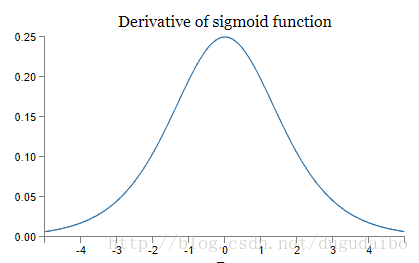
圖1. sigmoid函式導數的影象
在上面這個影象中,橫座標是 sigmoid 函式的輸入,即權值輸入 z ,而縱座標是啟用函式的輸出值的導數,我們可以看到,該導數
首先考慮還沒有開始訓練的初始狀態,如果我們使用標準方法來初始化網路中的權重,那麼會使用一個均值為 0 標準差為 1 的高斯分佈。因此所有的權重通常會滿足

圖2. 梯度的複合求導
可以看到在我們進行了所有這些項的乘積時,最終結果肯定會指數級下降:項越多,乘積的下降的越快。這裡我們敏銳地嗅到了梯度消失問題的合理解釋。
為了避免梯度消失問題,我們需要
也距離說明一下題都爆炸的原因。當權值輸入為0,但是引數
如果在某一個神經元出現了這樣的情況,那麼在複雜網路中根據反向傳播中的四個基本等式這也是同樣會出現的。
綜上,根本的問題其實並非是梯度消失問題或者激增的梯度問題,而是在前面的層上的梯度是來自後面的層上項的乘積。當存在過多的層次時,就出現了內在本質上的不穩定場景。唯一讓所有層都接近相同的學習速度的方式是所有這些項的乘積都能得到一種平衡。如果沒有某種機制或者更加本質的保證來達成平衡,那網路就很容易不穩定了。簡而言之,真實的問題就是神經網路受限於不穩定梯度的問題。所以,如果我們使用標準的基於梯度的學習演算法,在網路中的不同層會出現按照不同學習速度學習的情況。
如本篇部落格沒有解決你的問題可在評論區留言,如果能幫上的一定會幫助;
如果覺得解決了你的問題請頂一下 ~;
也歡迎指導、提問、留言~~~~
