機器學習演算法總結
機器學習(Machine Learning, ML)是一門多領域交叉學科,涉及概率論、統計學、逼近論、凸分析、演算法複雜度理論等多門學科。專門研究計算機怎樣模擬或實現人類的學習行為,以獲取新的知識或技能,重新組織已有的知識結構使之不斷改善自身的效能。
嚴格的定義:機器學習是一門研究機器獲取新知識和新技能,並識別現有知識的學問。這裡所說的“機器”,指的就是計算機,電子計算機,中子計算機、光子計算機或神經計算機等等。
機器學習概論
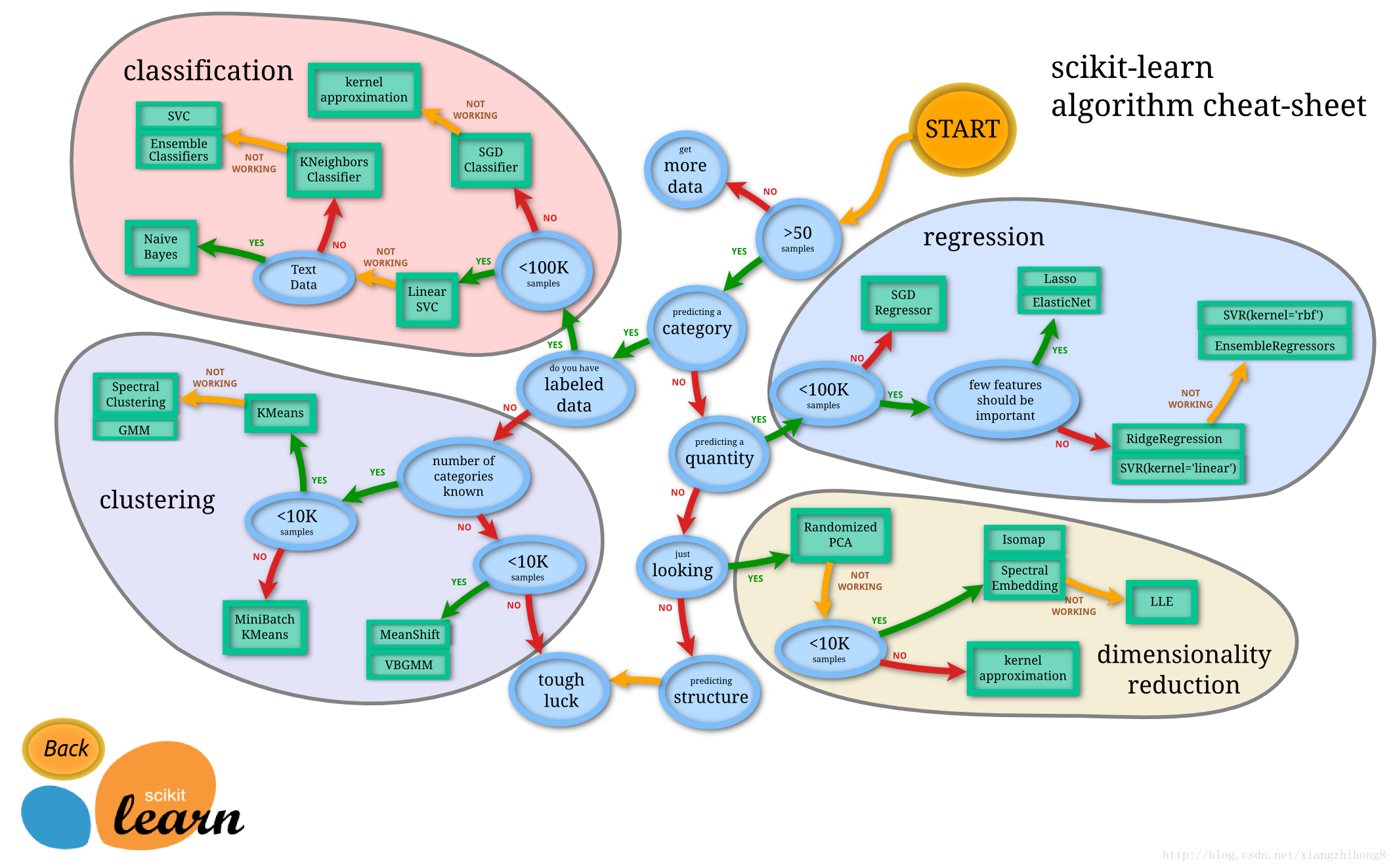
由上圖所示:機器學習分為四大塊: classification (分類), clustering (聚類),regression (迴歸),
dimensionality reduction (降維)
classification & regression
舉一個簡單的例子:
給定一個樣本特徵 x, 我們希望預測其對應的屬性值 y, 如果 y 是離散的, 那麼這就是一個分類問題,反之,如果 y 是連續的實數, 這就是一個迴歸問題。
如果給定一組樣本特徵 S={x∈RD}, 我們沒有對應的 y, 而是想發掘這組樣本在 D 維空間的分佈, 比如分析哪些樣本靠的更近,哪些樣本之間離得很遠, 這就是屬於聚類問題。
如果我們想用維數更低的子空間來表示原來高維的特徵空間, 那麼這就是降維問題。
無論是分類還是迴歸,都是想建立一個預測模型 H,給定一個輸入 x, 可以得到一個輸出 y:
y=H(x)
不同的只是在分類問題中, y 是離散的; 而在迴歸問題中 y 是連續的。所以總得來說,兩種問題的學習演算法都很類似。所以在這個圖譜上,我們看到在分類問題中用到的學習演算法,在迴歸問題中也能使用。分類問題最常用的學習演算法包括 SVM (支援向量機) , SGD (隨機梯度下降演算法), Bayes (貝葉斯估計), Ensemble, KNN 等。而回歸問題也能使用 SVR, SGD, Ensemble 等演算法,以及其它線性迴歸演算法。
clustering
聚類也是分析樣本的屬性, 有點類似classification, 不同的就是classification 在預測之前是知道 y 的範圍, 或者說知道到底有幾個類別, 而聚類是不知道屬性的範圍的。所以 classification 也常常被稱為 supervised learning, 而clustering就被稱為 unsupervised learning。
clustering 事先不知道樣本的屬性範圍,只能憑藉樣本在特徵空間的分佈來分析樣本的屬性。這種問題一般更復雜。而常用的演算法包括 k-means (K-均值), GMM (高斯混合模型) 等。
dimensionality reduction
降維是機器學習另一個重要的領域, 降維有很多重要的應用, 特徵的維數過高, 會增加訓練的負擔與儲存空間, 降維就是希望去除特徵的冗餘, 用更加少的維數來表示特徵. 降維演算法最基礎的就是PCA了, 後面的很多演算法都是以PCA為基礎演化而來。
機器 學習常見演算法
機器學習領域涉及到很多的演算法和模型,這裡遴選一些常見的演算法:
- 正則化演算法(Regularization Algorithms)
- 整合演算法(Ensemble Algorithms)
- 決策樹演算法(Decision Tree Algorithm)
- 迴歸(Regression)
- 人工神經網路(Artificial Neural Network)
- 深度學習(Deep Learning)
- 支援向量機(Support Vector Machine)
- 降維演算法(Dimensionality Reduction Algorithms)
- 聚類演算法(Clustering Algorithms)
- 基於例項的演算法(Instance-based Algorithms)
- 貝葉斯演算法(Bayesian Algorithms)
- 關聯規則學習演算法(Association Rule Learning Algorithms)
- 圖模型(Graphical Models)### 正則化演算法(Regularization Algorithms)正則化演算法是另一種方法(通常是迴歸方法)的拓展,這種方法會基於模型複雜性對其進行懲罰,它喜歡相對簡單能夠更好的泛化的模型。正則化中我們將保留所有的特徵變數,但是會減小特徵變數的數量級(引數數值的大小θ(j))。這個方法非常有效,當我們有很多特徵變數時,其中每一個變數都能對預測產生一點影響。演算法例項:
- 嶺迴歸(Ridge Regression)
- 最小絕對收縮與選擇運算元(LASSO)
- GLASSO
- 彈性網路(Elastic Net)
- 最小角迴歸(Least-Angle Regression)詳解連結:機器學習之正則化演算法
整合演算法(Ensemble algorithms)
整合方法是由多個較弱的模型整合模型組,其中的模型可以單獨進行訓練,並且它們的預測能以某種方式結合起來去做出一個總體預測。這類演算法又稱元演算法(meta-algorithm)。最常見的整合思想有兩種bagging和boosting。
boosting
基於錯誤提升分類器效能,通過集中關注被已有分類器分類錯誤的樣本,構建新分類器並整合。
bagging
基於資料隨機重抽樣的分類器構建方法。
演算法例項:
- Boosting
- Bootstrapped Aggregation(Bagging)
- AdaBoost
- 層疊泛化(Stacked Generalization)(blending)
- 梯度推進機(Gradient Boosting Machines,GBM)
- 梯度提升迴歸樹(Gradient Boosted Regression Trees,GBRT)
- 隨機森林(Random Forest)總結:當先最先進的預測幾乎都使用了演算法整合。它比使用單個模型預測出來的結果要精確的多。但是該演算法需要大量的維護工作。詳細講解:機器學習演算法之整合演算法### 決策樹演算法(Decision Tree Algorithm)決策樹學習使用一個決策樹作為一個預測模型,它將對一個 item(表徵在分支上)觀察所得對映成關於該 item 的目標值的結論(表徵在葉子中)。決策樹通過把例項從艮節點排列到某個葉子結點來分類例項,葉子結點即為例項所屬的分類。樹上的每一個結點指定了對例項的某個屬性的測試,並且該結點的每一個後繼分支對應於該屬性的一個可能值。分類例項的方法是從這棵樹的根節點開始,測試這個結點的屬性,然後按照給定例項的屬性值對應的樹枝向下移動。然後這個過程在以新結點的根的子樹上重複。演算法例項:
- 分類和迴歸樹(Classification and Regression Tree,CART)
- Iterative Dichotomiser 3(ID3)
- C4.5 和 C5.0(一種強大方法的兩個不同版本)詳解:機器學習演算法之決策樹演算法
迴歸(Regression)演算法
迴歸是用於估計兩種變數之間關係的統計過程。當用於分析因變數和一個 多個自變數之間的關係時,該演算法能提供很多建模和分析多個變數的技巧。具體一點說,迴歸分析可以幫助我們理解當任意一個自變數變化,另一個自變數不變時,因變數變化的典型值。最常見的是,迴歸分析能在給定自變數的條件下估計出因變數的條件期望。
演算法例項:
- 普通最小二乘迴歸(Ordinary Least Squares Regression,OLSR)
- 線性迴歸(Linear Regression)
- 邏輯迴歸(Logistic Regression)
- 逐步迴歸(Stepwise Regression)
- 多元自適應迴歸樣條(Multivariate Adaptive Regression Splines,MARS)
- 本地散點平滑估計(Locally Estimated Scatterplot Smoothing,LOESS)
人工神經網路
人工神經網路是受生物神經網路啟發而構建的演算法模型。它是一種模式匹配,常被用於迴歸和分類問題,但擁有龐大的子域,由數百種演算法和各類問題的變體組成。
人工神經網路(ANN)提供了一種普遍而且實際的方法從樣例中學習值為實數、離散值或向量函式。人工神經網路由一系列簡單的單元相互連線構成,其中每個單元有一定數量的實值輸入,併產生單一的實值輸出。
演算法例項:
- 感知器
- 反向傳播
- Hopfield 網路
- 徑向基函式網路(Radial Basis Function Network,RBFN)
深度學習(Deep Learning)
深度學習是人工神經網路的最新分支,它受益於當代硬體的快速發展。
眾多研究者目前的方向主要集中於構建更大、更復雜的神經網路,目前有許多方法正在聚焦半監督學習問題,其中用於訓練的大資料集只包含很少的標記。
演算法例項:
- 深玻耳茲曼機(Deep Boltzmann Machine,DBM)
- Deep Belief Networks(DBN)
- 卷積神經網路(CNN)
- Stacked Auto-Encoders
支援向量機(Support Vector Machines)
支援向量機是一種監督式學習 (Supervised Learning)的方法,主要用在統計分類 (Classification)問題和迴歸分析 (Regression)問題上。支援向量機屬於一般化線性分類器,也可以被認為是提克洛夫規範化(Tikhonov Regularization)方法的一個特例。這族分類器的特點是他們能夠同時最小化經驗誤差與最大化幾何邊緣區,因此支援向量機也被稱為最大邊緣區分類器。現在多簡稱為SVM。
給定一組訓練事例,其中每個事例都屬於兩個類別中的一個,支援向量機(SVM)訓練演算法可以在被輸入新的事例後將其分類到兩個類別中的一個,使自身成為非概率二進位制線性分類器。
SVM 模型將訓練事例表示為空間中的點,它們被對映到一幅圖中,由一條明確的、儘可能寬的間隔分開以區分兩個類別。
降維演算法(Dimensionality Reduction Algorithms)
所謂的降維就是指採用某種對映方法,將原高維空間中的資料點對映到低維度的空間中。降維的本質是學習一個對映函式 f : x->y,其中x是原始資料點的表達,目前最多使用向量表達形式。 y是資料點對映後的低維向量表達,通常y的維度小於x的維度(當然提高維度也是可以的)。f可能是顯式的或隱式的、線性的或非線性的。
這一演算法可用於視覺化高維資料或簡化接下來可用於監督學習中的資料。許多這樣的方法可針對分類和迴歸的使用進行調整。
演算法例項:
- 主成分分析(Principal Component Analysis (PCA))
- 主成分迴歸(Principal Component Regression (PCR))
- 偏最小二乘迴歸(Partial Least Squares Regression (PLSR))
- Sammon 對映(Sammon Mapping)
- 多維尺度變換(Multidimensional Scaling (MDS))
- 投影尋蹤(Projection Pursuit)
- 線性判別分析(Linear Discriminant Analysis (LDA))
- 混合判別分析(Mixture Discriminant Analysis (MDA))
- 二次判別分析(Quadratic Discriminant Analysis (QDA))
- 靈活判別分析(Flexible Discriminant Analysis (FDA))
詳解連結:降維演算法
聚類演算法(Clustering Algorithms)
聚類演算法是指對一組目標進行分類,屬於同一組(亦即一個類,cluster)的目標被劃分在一組中,與其他組目標相比,同一組目標更加彼此相似。
優點是讓資料變得有意義,缺點是結果難以解讀,針對不同的資料組,結果可能無用。
演算法例項:
- K-均值(k-Means)
- k-Medians 演算法
- Expectation Maximi 封層 ation (EM)
- 最大期望演算法(EM)
- 分層叢集(Hierarchical Clstering)
貝葉斯演算法(Bayesian Algorithms)
貝葉斯定理(英語:Bayes' theorem)是概率論中的一個定理,它跟隨機變數的條件概率以及邊緣概率分佈有關。在有些關於概率的解說中,貝葉斯定理(貝葉斯更新)能夠告知我們如何利用新證據修改已有的看法。貝葉斯方法是指明確應用了貝葉斯定理來解決如分類和迴歸等問題的方法。
演算法例項:
- 樸素貝葉斯(Naive Bayes)
- 高斯樸素貝葉斯(Gaussian Naive Bayes)
- 多項式樸素貝葉斯(Multinomial Naive Bayes)
- 平均一致依賴估計器(Averaged One-Dependence Estimators (AODE))
- 貝葉斯信念網路(Bayesian Belief Network (BBN))
- 貝葉斯網路(Bayesian Network (BN))
關聯規則學習演算法(Association Rule Learning Algorithms)
關聯規則學習方法能夠提取出對資料中的變數之間的關係的最佳解釋。比如說一家超市的銷售資料中存在規則 {洋蔥,土豆}=> {漢堡},那說明當一位客戶同時購買了洋蔥和土豆的時候,他很有可能還會購買漢堡肉。有點類似於聯想演算法。
演算法例項:
- Apriori 演算法(Apriori algorithm)
- Eclat 演算法(Eclat algorithm)
- FP-growth
圖模型(Graphical Models)
圖模型(GraphicalModels)在概率論與圖論之間建立起了聯姻關係。它提供了一種自然工具來處理應用數學與工程中的兩類問題——不確定性(Uncertainty)和複雜性(Complexity)問 題,特別是在機器學習演算法的分析與設計中扮演著重要角色。圖模型的基本理念是模組化的思想,複雜系統是通過組合簡單系統建構的。概率論提供了一種粘合劑使 系統的各個部分組合在一起,確保系統作為整體的持續一致性,提供了多種資料介面模型方法。
圖模型或概率圖模型(PGM/probabilistic graphical model)是一種概率模型,一個圖(graph)可以通過其表示隨機變數之間的條件依賴結構(conditional dependence structure)。
演算法例項:
- 貝葉斯網路(Bayesian network)
- 馬爾可夫隨機域(Markov random field)
- 鏈圖(Chain Graphs)
- 祖先圖(Ancestral graph)