特徵生成

特徵工程中引入的新特徵，需要驗證它確實能提高預測得準確度，而不是加入一個無用的特徵增加演算法運算的複雜度。

1. 時間戳處理

時間戳屬性通常需要分離成多個維度比如年、月、日、小時、分鐘、秒鐘。但是在很多的應用中，大量的資訊是不需要的。比如在一個監督系統中，嘗試利用一個’位置+時間‘的函式預測一個城市的交通故障程度，這個例項中，大部分會受到誤導只通過不同的秒數去學習趨勢，其實是不合理的。並且維度’年’也不能很好的給模型增加值的變化，我們可能僅僅需要小時、日、月等維度。因此在呈現時間的時候，試著保證你所提供的所有資料是你的模型所需要的。並且別忘了時區，假如你的資料來源來自不同的地理資料來源，別忘了利用時區將資料標準化。

2. 分解類別屬性(one-hot)

一些屬性是類別型而不是數值型，舉一個簡單的例子，由{紅，綠、藍}組成的顏色屬性，最常用的方式是把每個類別屬性轉換成二元屬性，即從{0,1}取一個值。因此基本上增加的屬性等於相應數目的類別，並且對於你資料集中的每個例項，只有一個是1（其他的為0），這也就是獨熱（one-hot)編碼方式（類似於轉換成啞變數）。
如果你不瞭解這個編碼的話，你可能會覺得分解會增加沒必要的麻煩（因為編碼大量的增加了資料集的維度）。相反，你可能會嘗試將類別屬性轉換成一個標量值，例如顏色屬性可能會用{1,2,3}表示{紅，綠，藍}。這裡存在兩個問題，首先，對於一個數學模型，這意味著某種意義上紅色和綠色比和藍色更“相似”（因為|1-3| > |1-2|）。除非你的類別擁有排序的屬性

（比如鐵路線上的站），這樣可能會誤導你的模型。然後，可能會導致統計指標（比如均值）無意義，更糟糕的情況是，會誤導你的模型。還是顏色的例子，假如你的資料集包含相同數量的紅色和藍色的例項，但是沒有綠色的，那麼顏色的均值可能還是得到2，也就是綠色的意思。
能夠將類別屬性轉換成一個標量，最有效的場景應該就是隻有兩個類別的情況。即{0,1}對應{類別1，類別2}。這種情況下，並不需要排序，並且你可以將屬性的值理解成屬於類別1或類別2的概率。

3.分箱/分割槽(數值型轉類別型)

有時候，將數值型屬性轉換成類別型更有意義，同時將一定範圍內的數值劃分成確定的塊，使演算法減少噪聲的干擾。只有在瞭解屬性的領域知識的基礎，確定屬效能夠劃分成簡潔的範圍時分割槽才有意義，即所有的數值落入一個分割槽時能夠呈現出共同的特徵。

在實際應用中，當你不想讓你的模型總是嘗試區分值之間是否太近時，分割槽能夠避免過擬合。例如，如果你所感興趣的是將一個城市作為整體，這時你可以將所有落入該城市的維度值進行整合成一個整體。分箱也能減小小錯誤的影響，通過將一個給定值劃入到最近的塊中。如果劃分範圍的數量和所有可能值相近，或對你來說準確率很重要的話，此時分箱就不適合了。

4. 交叉特徵(組合分類特徵)

交叉特徵算是特徵工程中非常重要的方法之一了，它是將兩個或更多的類別屬性組合成一個。當組合的特徵要比單個特徵更好時，這是一項非常有用的技術。數學上來說，是對類別特徵的所有可能值進行交叉相乘。假如擁有一個特徵A,A有兩個可能值{A1，A2}。擁有一個特徵B，存在{B1，B2}等可能值。然後，A&B之間的交叉特徵如下：{（A1，B1），（A1，B2），（A2，B1），（A2，B2）}，並且你可以給這些組合特徵取任何名字，但是需要明白每個組合特徵其實代表著A和B各自資訊協同作用。一個更好地詮釋好的交叉特徵的例項是類似於（經度，緯度）。一個相同的經度對應了地圖上很多的地方，緯度也是一樣。但是一旦你將經度和緯度組合到一起，它們就代表了地理上特定的一塊區域，區域中每一部分是擁有著類似的特性。

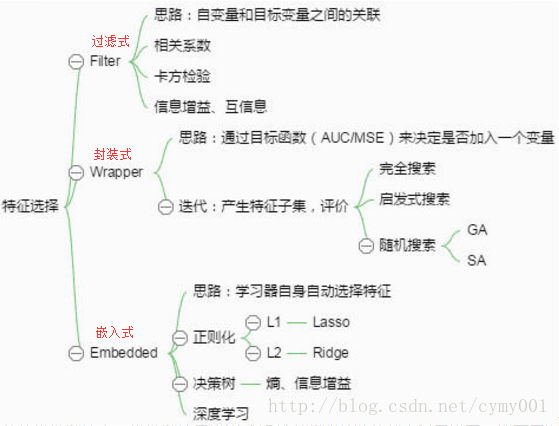
5. 特徵選擇

為了得到更好的模型，使用某些演算法自動的選出原始特徵的子集。這個過程，你不會構建或修改你擁有的特徵，但是會通過修剪特徵來達到減少噪聲和冗餘。在資料特徵中，存在一些對於提高模型的準確率比其他更重要的特徵，也還有一些與其他特徵放在一起出現了冗餘，特徵選擇是自動選出對於解決問題最有用的特徵子集來解決上述問題的。特徵選擇演算法可能會用評分方法排名和選擇特徵，比如相關性或其他確定特徵重要性的方法，更進一步的方法可能需要通過試錯，來搜尋出特徵子集。
還可以構建輔助模型，逐步迴歸就是模型構造過程中自動執行特徵選擇演算法的一個例項，還有像Lasso迴歸和嶺迴歸等正則化方法也被歸入到特徵選擇，通過加入額外的約束或者懲罰項加到已有模型（損失函式）上，以防止過擬合併提高泛化能力。

6. 特徵縮放

某些特徵比其他特徵具有較大的跨度值。舉個例子，將一個人的收入和他的年齡進行比較，更具體的例子，如某些模型（像嶺迴歸）要求你必須將特徵值縮放到相同的範圍值內。通過縮放可以避免某些特徵比其他特徵獲得大小非常懸殊的權重值。

7. 特徵提取

特徵提取涉及到從原始屬性中自動生成一些新的特徵集的一系列演算法，降維演算法就屬於這一類。特徵提取是一個自動將觀測值降維到一個足夠建模的小資料集的過程。對於列表資料，可使用的方法包括一些投影方法，像主成分分析和無監督聚類演算法。對於圖形資料，可能包括一些直線檢測和邊緣檢測，對於不同領域有各自的方法。
特徵提取的關鍵點在於這些方法是自動的（只需要從簡單方法中設計和構建得到），還能夠解決不受控制的高維資料的問題。大部分的情況下，是將這些不同型別資料（如圖，語言，視訊等）存成數字格式來進行模擬觀察。

特徵選擇

(1)子集產生：按照一定的搜尋策略產生候選特徵子集；
(2)子集評估：通過某個評價函式評估特徵子集的優劣；
(3)停止條件：決定特徵選擇演算法什麼時候停止；
(4)子集驗證：用於驗證最終所選的特徵子集的有效性。

特徵選擇的搜尋策略分為：完全搜尋策略、啟發式策略以及隨機搜尋策略。
特徵選擇本質上是一個組合優化問題，求解組合優化問題最直接的方法就是搜尋，理論上可以通過窮舉法來搜尋所有可能的特徵組合，選擇使得評價標準最優的特徵子集作為最後的輸出，但是n個特徵的搜尋空間為2n，窮舉法的運算量隨著特徵維數的增加呈指數遞增，實際應用中經常碰到幾百甚至成千上萬個特徵，因此窮舉法雖然簡單卻難以實際應用。其他的搜尋方法有啟發式搜尋和隨機搜尋，這些搜尋策略可以在運算效率和特徵子集質量之間尋找到一個較好的平衡點，而這也是眾多特徵選擇演算法努力的目標。

完全搜尋(Complete)

廣度優先搜尋( Breadth First Search )：廣度優先遍歷特徵子空間。列舉所有組合，窮舉搜尋，實用性不高。
分支限界搜尋( Branch and Bound )：窮舉基礎上加入分支限界。例如：剪掉某些不可能搜尋出比當前最優解更優的分支。
其他，如定向搜尋 (Beam Search )，最優優先搜尋 ( Best First Search )等。

啟發式搜尋(Heuristic)

序列前向選擇(SFS，Sequential Forward Selection)：從空集開始，每次加入一個選最優。
序列後向選擇(SBS，Sequential Backward Selection)：從全集開始，每次減少一個選最優。
增L去R選擇演算法 (LRS，Plus-L Minus-R Selection)：從空集開始，每次加入L$L$個，減去R$R$個，選最優(L>R$L>R$)或者從全集開始，每次減去R$R$個，增加L$L$個，選最優(L<R$L<R$)。
其他，如雙向搜尋(BDS，Bidirectional Search)，序列浮動選擇(Sequential Floating Selection)等。

隨機搜尋(Random)

隨機產生序列選擇演算法(RGSS， Random Generation plus Sequential Selection)：隨機產生一個特徵子集，然後在該子集上執行SFS與SBS演算法。
模擬退火演算法( SA， Simulated Annealing )：以一定的概率接受一個比當前解要差的解，而且這個概率隨著時間推移逐漸降低。
遺傳演算法( GA， Genetic Algorithms )：通過交叉、突變等操作繁殖出下一代特徵子集，並且評分越高的特徵子集被選中參加繁殖的概率越高。
隨機演算法共同缺點:依賴隨機因素，實驗結果難重現。

Embedded：在嵌入式特徵選擇中，特徵選擇演算法本身作為組成部分嵌入到學習演算法裡。最典型的即決策樹演算法，如ID3、C4.5以及CART演算法等，決策樹演算法在樹增長過程的每個遞迴步都必須選擇一個特徵，將樣本集劃分成較小的子集，選擇特徵的依據通常是劃分後子節點的純度，劃分後子節點越純，則說明劃分效果越好，可見決策樹生成的過程也就是特徵選擇的過程。

Filter：過濾式特徵選擇的評價標準從資料集本身的內在性質獲得，與特定的學習演算法無關，因此具有較好的通用性。通常選擇和類別相關度大的特徵或者特徵子集。過濾式特徵選擇的研究者認為，相關度較大的特徵或者特徵子集會在分類器上獲得較高的準確率。過濾式特徵選擇的評價標準分為四種，即距離度量、資訊度量、關聯度度量以及一致性度量。
優點：演算法的通用性強；省去了分類器的訓練步驟，演算法複雜性低，因而適用於大規模資料集；可以快速去除大量不相關的特徵，作為特徵的預篩選器非常合適。缺點：由於演算法的評價標準獨立於特定的學習演算法，所選的特徵子集在分類準確率方面通常低於Wrapper方法。

Wrapper：封裝式特徵選擇是利用學習演算法的效能評價特徵子集的優劣。因此，對於一個待評價的特徵子集，Wrapper方法需要訓練一個分類器，根據分類器的效能對該特徵子集進行評價。Wrapper方法中用以評價特徵的學習演算法是多種多樣的，例如決策樹、神經網路、貝葉斯分類器、近鄰法、支援向量機等等。
優點：相對於Filter方法，Wrapper方法找到的特徵子集分類效能通常更好。缺點：Wrapper方法選出的特徵通用性不強，當改變學習演算法時，需要針對該學習演算法重新進行特徵選擇；由於每次對子集的評價都要進行分類器的訓練和測試，所以演算法計算複雜度很高，尤其對於大規模資料集來說，演算法的執行時間很長。

非監督特徵學習的目標是捕捉高維資料中的底層結構，挖掘出低維的特徵。
在特徵學習中，K-means演算法可以將一些沒有標籤的輸入資料進行聚類，然後使用每個類別的質心來生成新的特徵。