Improvise a Jazz Solo with an LSTM Network

​
Welcome to your final programming assignment of this week! In this notebook, you will implement a model that uses an LSTM to generate music. You will even be able to listen to your own music at the end of the assignment.
​
You will learn to:

• Apply an LSTM to music generation. （使用LSTM來生成音樂）
• Generate your own jazz music with deep learning.（通過深度學習來生成自己的Jazz音樂）
  ​
  Please run the following cell to load all the packages required in this assignment. This may take a few minutes.

from __future__ import print_function
import IPython
import sys
from music21 import *
import numpy as np
from grammar import *
from qa import *
from preprocess import * 
from music_utils import *
from data_utils import *
from keras.models import load_model, Model
from keras.layers import Dense, Activation, Dropout, Input, LSTM, Reshape, Lambda, RepeatVector
from keras.initializers import glorot_uniform
from keras.utils import to_categorical
from keras.optimizers import Adam
from keras import backend as K
 

1 - Problem statement

You would like to create a jazz music piece specially for a friend’s birthday. However, you don’t know any instruments or music composition. Fortunately, you know deep learning and will solve this problem using an LSTM netwok.

You will train a network to generate novel jazz solos in a style representative of a body of performed work.

1.1 - Dataset

You will train your algorithm on a corpus of Jazz music. Run the cell below to listen to a snippet of the audio from the training set:

（你將在Jazz music中的語料庫中訓練你的演算法，執行下面程式碼播放訓練集中的一小段音樂）

IPython.display.Audio('./data/30s_seq.mp3')

We have taken care of the preprocessing of the musical data to render it in terms of musical “values.” You can informally think of each “value” as a note, which comprises a pitch and a duration. For example, if you press down a specific piano key for 0.5 seconds, then you have just played a note. In music theory, a “value” is actually more complicated than this–specifically, it also captures the information needed to play multiple notes at the same time. For example, when playing a music piece, you might press down two piano keys at the same time (playng multiple notes at the same time generates what’s called a “chord”). But we don’t need to worry about the details of music theory for this assignment. For the purpose of this assignment, all you need to know is that we will obtain a dataset of values, and will learn an RNN model to generate sequences of values.

（我們對音樂資料進行了預處理通過音樂‘值’來解釋它。你可以非正式的將每個值看作是一個音符，包括一個高音和一個持續時間。例如，如果你按下一個特定的鋼琴鍵0.5秒，那麼你就播放了一個音符。在音樂理論中，‘值’要更加複雜，具體地，它也可以從多個同時播放的音符來捕捉資訊。例如，當演奏一段音樂片段，你需要同時按下倆個鋼琴的鍵（同時播放多個音符，產生所謂的‘和絃’）。但我們不需要擔心音樂理論的細節。為了完成這個任務，你需要知道的是，我們將獲取‘值’的資料集，我們通過學習RNN模型來生成‘值’的序列。）

Our music generation system will use 78 unique values. Run the following code to load the raw music data and preprocess it into values. This might take a few minutes.

（我們音樂生成系統將使用78個不同的‘值’,執行下面的程式碼來匯入原生的音樂資料和將他們預處理成‘值’，這將需要花費幾分鐘）

X, Y, n_values, indices_values = load_music_utils()  #data/original_metheny.mid
print('shape of X:', X.shape)
print('number of training examples:', X.shape[0]) #訓練的樣本數
print('Tx (length of sequence):', X.shape[1]) #一段sequence的長度，即x^{1}->x^{30}
print('total # of unique values:', n_values)  #n_values,代表這段音訊可以用多少個值來代替
print('Shape of Y:', Y.shape)

Output:

shape of X: (60, 30, 78)
number of training examples: 60
Tx (length of sequence): 30
total # of unique values: 78
Shape of Y: (30, 60, 78)

You have just loaded the following:

• X: This is an (m, $T_x$, 78) dimensional array. We have m training examples, each of which is a snippet of $T_x =30$ musical values. At each time step, the input is one of 78 different possible values, represented as a one-hot vector. Thus for example, X[i,t,:] is a one-hot vector representating the value of the i-th example at time t.

'X’是一個(m,$T_x$,78)維度的矩陣。我們有m個訓練樣本，每一樣本都有$T_x=30$個的音樂‘值’集。在每一個時間步長中，輸入為78個不同的可能值中的一個，是一個one-hot vector。因此，對於 X[i,t,:]是一個one-hot向量代表著第i個樣本在t時間段的值。

• Y: This is essentially the same as X, but shifted one step to the left (to the past). Similar to the dinosaurus assignment, we’re interested in the network using the previous values to predict the next value, so our sequence model will try to predict $y^{\langle t \rangle}$ given $x^{\langle 1\rangle}, \ldots, x^{\langle t \rangle}$. However, the data in Y is reordered to be dimension $(T_y, m, 78)$, where $T_y = T_x$. This format makes it more convenient to feed to the LSTM later.

'Y’與上一個作業一樣，其值與X的值是一樣的，但是向左平移了一個位置（即y^{t}=x{t+1}）。我們使用前一個的輸出值來預測下一個值，因此我們的模型將會嘗試去預測$y^{\langle t \rangle}$,通過給定 $x^{\langle 1\rangle}, \ldots, x^{\langle t \rangle}$。然而，資料 ‘Y’被重新組織成 $（T_y,m,78）$，T_y=T_x,這有利於後面的LSTM的輸入。（儘管到這裡我還不知道為什麼）

• n_values: The number of unique values in this dataset. This should be 78.

（n_values 在這個資料集上不同值的數量，這裡應該是78）

• indices_values: python dictionary mapping from 0-77 to musical values.
  （indices_values: 使用python字典，將musical values對映成 0-77 的數字）

1.2 - Overview of our model

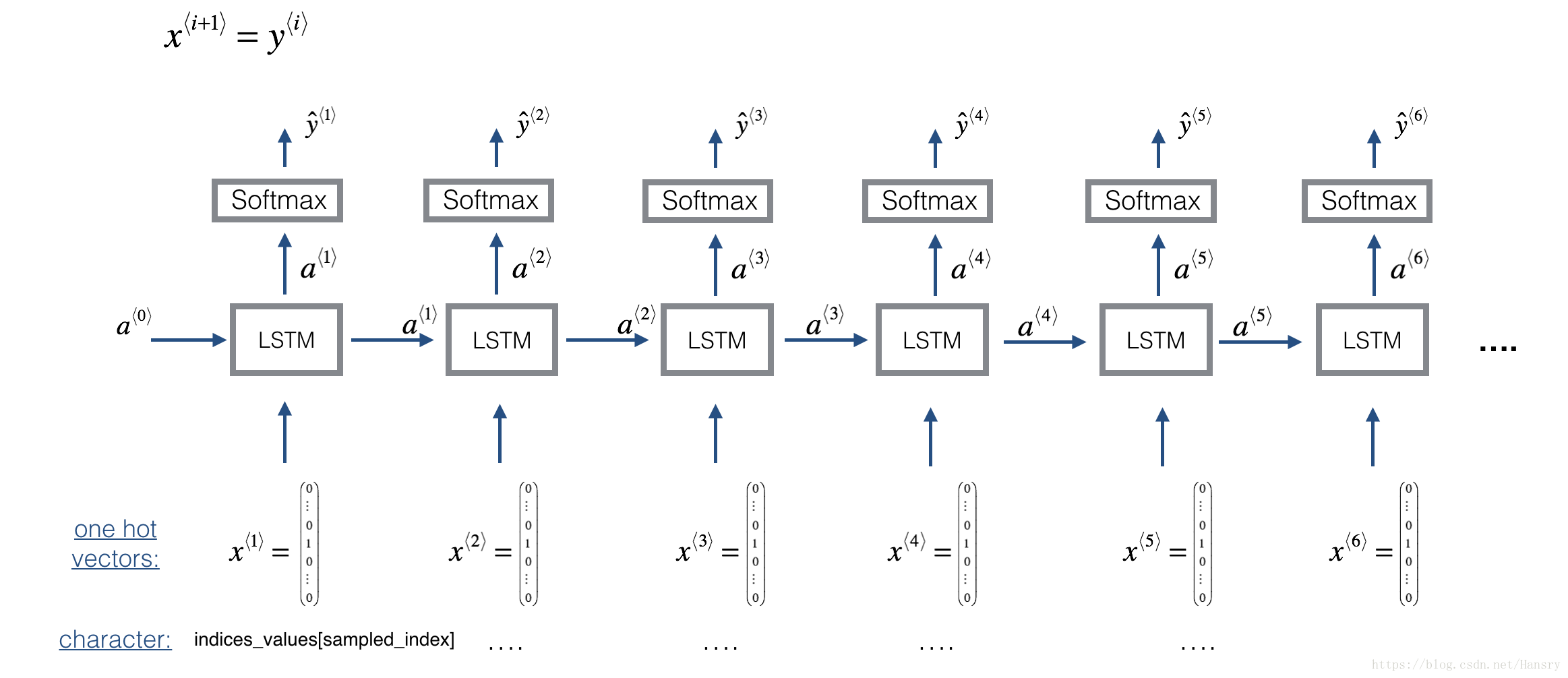
Here is the architecture of the model we will use. This is similar to the Dinosaurus model you had used in the previous notebook, except that in you will be implementing it in Keras. The architecture is as follows:

（下面的模型是我們將會用到的，這個跟我們前面用到的Dinosaurus model很相似，但是接下來我們會用keras來執行，模型的結構如下所示：）

We will be training the model on random snippets of 30 values taken from a much longer piece of music. Thus, we won’t bother to set the first input $x^{\langle 1 \rangle} = \vec{0}$, which we had done previously to denote the start of a dinosaur name, since now most of these snippets of audio start somewhere in the middle of a piece of music. We are setting each of the snippts to have the same length $T_x = 30$ to make vectorization easier.

2 - Building the model

In this part you will build and train a model that will learn musical patterns. To do so, you will need to build a model that takes in X of shape $(m, T_x, 78)$ and Y of shape $(T_y, m, 78)$. We will use an LSTM with 64 dimensional hidden states. Lets set n_a = 64.

n_a = 64 

Here’s how you can create a Keras model with multiple inputs and outputs. If you’re building an RNN where even at test time entire input sequence $x^{\langle 1 \rangle}, x^{\langle 2 \rangle}, \ldots, x^{\langle T_x \rangle}$ were given in advance, for example if the inputs were words and the output was a label, then Keras has simple built-in functions to build the model. However, for sequence generation, at test time we don’t know all the values of $x^{\langle t\rangle}$ in advance; instead we generate them one at a time using $x^{\langle t\rangle} = y^{\langle t-1 \rangle}$. So the code will be a bit more complicated, and you’ll need to implement your own for-loop to iterate over the different time steps.

The function djmodel() will call the LSTM layer $T_x$ times using a for-loop, and it is important that all $T_x$ copies have the same weights. I.e., it should not re-initiaiize the weights every time—the $T_x$ steps should have shared weights. The key steps for implementing layers with shareable weights in Keras are:

（函式‘djmodel()’將在$T_x$中的每一個時間步使用for迴圈來呼叫LSTM層，值得強調的是所有的$T_x$擁有相同的權重，不應該在每一個時間步重新初始化權重。每一個時間步應該共享其權重。在Keras中執行權重共享的關鍵步驟為：

1. Define the layer objects (we will use global variables for this).#定義層物件（我們將會使用全域性變數）
2. Call these objects when propagating the input. #當傳播輸入的時候呼叫這些物件

We have defined the layers objects you need as global variables. Please run the next cell to create them. Please check the Keras documentation to make sure you understand what these layers are: Reshape(), LSTM(), Dense().

reshapor = Reshape((1, 78))                        # 例項化一些物件，初始化引數為(1,78) Used in Step 2.B of djmodel(), below
LSTM_cell = LSTM(n_a, return_state = True)         # Used in Step 2.C
densor = Dense(n_values, activation='softmax')     # Used in Step 2.D

Each of reshapor, LSTM_cell and densor are now layer objects, and you can use them to implement djmodel(). In order to propagate a Keras tensor object X through one of these layers, use layer_object(X) (or layer_object([X,Y]) if it requires multiple inputs.). For example, reshapor(X) will propagate X through the Reshape((1,78)) layer defined above.

（每一個‘reshapor’，‘LSTM_cell’和‘densor’現在是layer物件，可以簡單的使用它們來執行’djmodel()‘這個函式，為了使Keras中的張量X在這些layer中進行傳播，可以使用’layer_object(X)’（或者’layer_object([X,Y])'如果需要傳播多個輸入的時候）例如，‘reshapor(X)’ 將會在前面提到的Reshape(1,78)layer中進行傳播）

Exercise: Implement djmodel(). You will need to carry out 2 steps:

Create an empty list “outputs” to save the outputs of the LSTM Cell at every time step. （建立空的列表來儲存每一個時間步LSTM Cell的輸出）

Loop for t∈1,…,Txt∈1,…,Tx : ( for t in range(T_x) )

A. Select the "t"th time-step vector from X. The shape of this selection should be (78,). To do so, create a custom Lambda layer in Keras by using this line of code: (從X中選取第‘t’時間步的向量，該向量維度應該是(78,)，為了實現該效果，利用Kears中的Lambda來實現）

x = Lambda(lambda x: X[:,t,:])(X)

Look over the Keras documentation to figure out what this does. It is creating a “temporary” or “unnamed” function (that’s what Lambda functions are) that extracts out the appropriate one-hot vector, and making this function a Keras Layer object to apply to X.

B. Reshape x to be (1,78). You may find the reshapor() layer (defined below) helpful.
(將向量x reshape成（1,78））

C. Run x through one step of LSTM_cell. Remember to initialize the LSTM_cell with the previous step’s hidden state $a$ and cell state $c$. Use the following formatting:

(在LSTM_cell傳播x，使用上一步的狀態 a 和 c 來初始化LSTM_cell)
a, _, c = LSTM_cell(input_x, initial_state=[previous hidden state, previous cell state])
D. Propagate the LSTM’s output activation value through a dense+softmax layer using densor.

E. Append the predicted value to the list of “outputs”

# GRADED FUNCTION: djmodel

def djmodel(Tx, n_a, n_values):
    """
    Implement the model
    
    Arguments:
    Tx -- length of the sequence in a corpus
    n_a -- the number of activations used in our model
    n_values -- number of unique values in the music data 
    
    Returns:
    model -- a keras model with the 
    """
    
    # Define the input of your model with a shape 
    X = Input(shape=(Tx, n_values)) #將輸入reshape為(Tx,n_values)
    
    # Define s0, initial hidden state for the decoder LSTM
    a0 = Input(shape=(n_a,), name='a0')  #將輸入reshape為(n_a,)
    c0 = Input(shape=(n_a,), name='c0')  #將輸入reshape為(n_a,)
    a = a0
    c = c0
    
    ### START CODE HERE ### 
    # Step 1: Create empty list to append the outputs while you iterate (≈1 line)
    outputs = []
    
    # Step 2: Loop
    for t in range(Tx):
        
        # Step 2.A: select the "t"th time step vector from X. 
        x = Lambda(lambda x: X[:,t,:])(X)
        # Step 2.B: Use reshapor to reshape x to be (1, n_values) (≈1 line)
        x = reshapor(x)
        # Step 2.C: Perform one step of the LSTM_cell
        a, _, c = LSTM_cell(x, initial_state=[a, c])
        # Step 2.D: Apply densor to the hidden state output of LSTM_Cell
        out = densor(a)
        # Step 2.E: add the output to "outputs"
        outputs.append(out)
        
    # Step 3: Create model instance
    model = Model(input=[X, a0, c0], outputs=outputs) #定義模型
    
    ### END CODE HERE ###
    
    return model

Run the following cell to define your model. We will use Tx=30, n_a=64 (the dimension of the LSTM activations), and n_values=78. This cell may take a few seconds to run.

model = djmodel(Tx = 30 , n_a = 64, n_values = 78)  #初始化模型引數,一個樣本為30個time-setp,即有30個音符

You now need to compile your model to be trained. We will Adam and a categorical cross-entropy loss.

opt = Adam(lr=0.01, beta_1=0.9, beta_2=0.999, decay=0.01)  #模型優化方式
 
model.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy']) #模型編譯  

Finally, lets initialize a0 and c0 for the LSTM’s initial state to be zero.

m = 60  #這裡有60個樣本
a0 = np.zeros((m, n_a))
c0 = np.zeros((m, n_a))

Lets now fit the model! We will turn Y to a list before doing so, since the cost function expects Y to be provided in this format (one list item per time-step). So list(Y) is a list with 30 items, where each of the list items is of shape (60,78). Lets train for 100 epochs. This will take a few minutes.

讓我們現在 fit 模型！ 在這樣做之前，我們將把Y 變成一個列表，因為代價函式期望Y以這種格式輸出（每個時間步一個列表項）。 所以list（Y）是一個包含 30 個專案的列表，其中每個列表專案都是形狀的（60,78）。 讓訓練100個epochs。 這將需要幾分鐘的時間。

model.fit([X, a0, c0], list(Y), epochs=100)

Output:

Epoch 1/100
60/60 [==============================] - 0s - loss: 4.7687 - dense_1_loss_1: 3.5756 - dense_1_loss_2: 0.7726 - dense_1_loss_3: 0.1530 - dense_1_loss_4: 0.0337 - dense_1_loss_5: 0.0219 - dense_1_loss_6: 0.0147 - dense_1_loss_7: 0.0119 - dense_1_loss_8: 0.0111 - dense_1_loss_9: 0.0094 - dense_1_loss_10: 0.0090 - dense_1_loss_11: 0.0093 - dense_1_loss_12: 0.0080 - dense_1_loss_13: 0.0072 - dense_1_loss_14: 0.0082 - dense_1_loss_15: 0.0081 - dense_1_loss_16: 0.0077 - dense_1_loss_17: 0.0076 - dense_1_loss_18: 0.0077 - dense_1_loss_19: 0.0082 - dense_1_loss_20: 0.0077 - dense_1_loss_21: 0.0080 - dense_1_loss_22: 0.0079 - dense_1_loss_23: 0.0072 - dense_1_loss_24: 0.0077 - dense_1_loss_25: 0.0090 - dense_1_loss_26: 0.0082 - dense_1_loss_27: 0.0086 - dense_1_loss_28: 0.0095 - dense_1_loss_29: 0.0101 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.7333 - dense_1_acc_3: 0.9667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00  

... ...
Epoch 100/100
60/60 [==============================] - 0s - loss: 4.4084 - dense_1_loss_1: 3.4707 - dense_1_loss_2: 0.6597 - dense_1_loss_3: 0.1190 - dense_1_loss_4: 0.0204 - dense_1_loss_5: 0.0131 - dense_1_loss_6: 0.0086 - dense_1_loss_7: 0.0071 - dense_1_loss_8: 0.0065 - dense_1_loss_9: 0.0057 - dense_1_loss_10: 0.0052 - dense_1_loss_11: 0.0055 - dense_1_loss_12: 0.0048 - dense_1_loss_13: 0.0043 - dense_1_loss_14: 0.0048 - dense_1_loss_15: 0.0048 - dense_1_loss_16: 0.0046 - dense_1_loss_17: 0.0045 - dense_1_loss_18: 0.0046 - dense_1_loss_19: 0.0049 - dense_1_loss_20: 0.0046 - dense_1_loss_21: 0.0047 - dense_1_loss_22: 0.0047 - dense_1_loss_23: 0.0043 - dense_1_loss_24: 0.0046 - dense_1_loss_25: 0.0053 - dense_1_loss_26: 0.0048 - dense_1_loss_27: 0.0049 - dense_1_loss_28: 0.0056 - dense_1_loss_29: 0.0061 - dense_1_loss_30: 0.0000e+00 - dense_1_acc_1: 0.1000 - dense_1_acc_2: 0.7333 - dense_1_acc_3: 0.9667 - dense_1_acc_4: 1.0000 - dense_1_acc_5: 1.0000 - dense_1_acc_6: 1.0000 - dense_1_acc_7: 1.0000 - dense_1_acc_8: 1.0000 - dense_1_acc_9: 1.0000 - dense_1_acc_10: 1.0000 - dense_1_acc_11: 1.0000 - dense_1_acc_12: 1.0000 - dense_1_acc_13: 1.0000 - dense_1_acc_14: 1.0000 - dense_1_acc_15: 1.0000 - dense_1_acc_16: 1.0000 - dense_1_acc_17: 1.0000 - dense_1_acc_18: 1.0000 - dense_1_acc_19: 1.0000 - dense_1_acc_20: 1.0000 - dense_1_acc_21: 1.0000 - dense_1_acc_22: 1.0000 - dense_1_acc_23: 1.0000 - dense_1_acc_24: 1.0000 - dense_1_acc_25: 1.0000 - dense_1_acc_26: 1.0000 - dense_1_acc_27: 1.0000 - dense_1_acc_28: 1.0000 - dense_1_acc_29: 1.0000 - dense_1_acc_30: 0.0000e+00     
   

從上面可以看出，訓練樣本有60個樣本，對每個樣本進行了100次的迭代。

You should see the model loss going down. Now that you have trained a model, lets go on the the final section to implement an inference algorithm, and generate some music!

3 - Generating music

You now have a trained model which has learned the patterns of the jazz soloist. Lets now use this model to synthesize new music.

3.1 - Predicting & Sampling

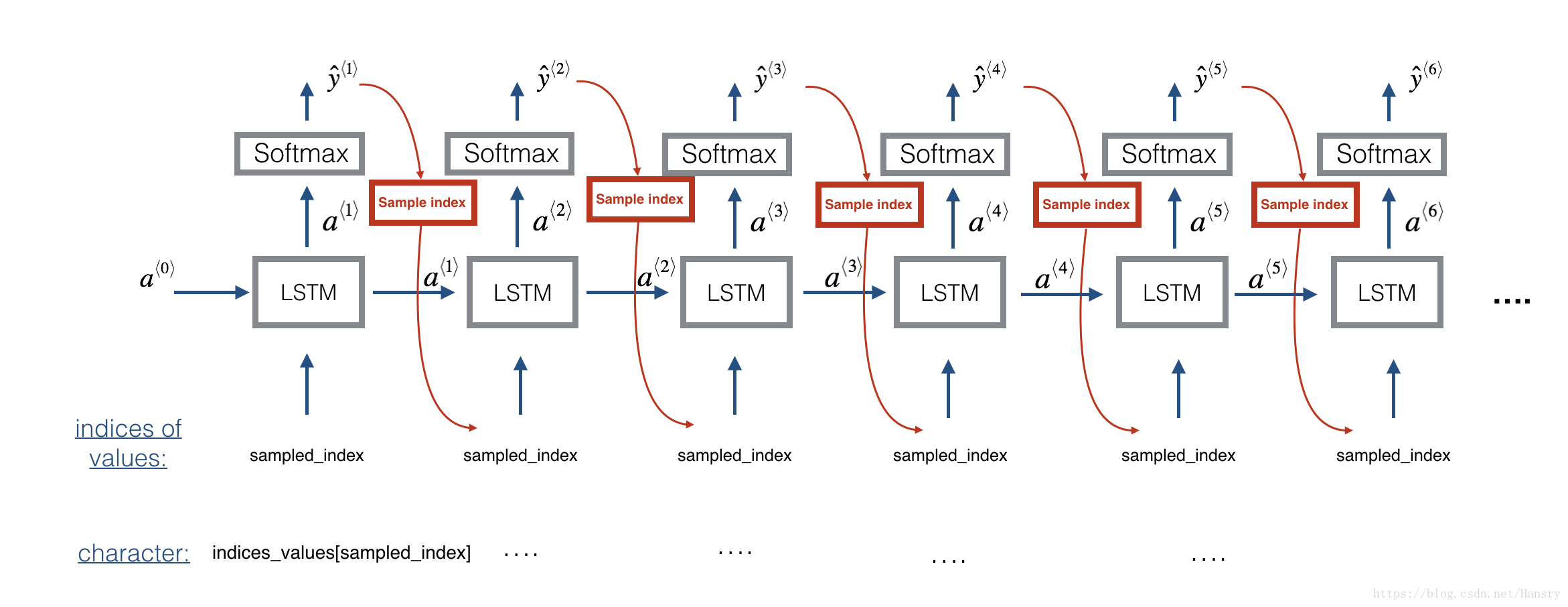
At each step of sampling, you will take as input the activation a and cell state c from the previous state of the LSTM, forward propagate by one step, and get a new output activation as well as cell state. The new activation a can then be used to generate the output, using densor as before.

To start off the model, we will initialize x0 as well as the LSTM activation and and cell value a0 and c0 to be zeros.

(首先先將 x0，a0，c0初始化為0)

Exercise: Implement the function below to sample a sequence of musical values. Here are some of the key steps you’ll need to implement inside the for-loop that generates the $T_y$ output characters:

Step 2.A: Use LSTM_Cell, which inputs the previous step’s c and a to generate the current step’s c and a.

Step 2.B: Use densor (defined previously) to compute a softmax on a to get the output for the current step.

Step 2.C: Save the output you have just generated by appending it to outputs.

Step 2.D: Sample x to the be “out”'s one-hot version (the prediction) so that you can pass it to the next LSTM’s step. We have already provided this line of code, which uses a Lambda function.

x = Lambda(one_hot)(out) 

[Minor technical note: Rather than sampling a value at random according to the probabilities in out, this line of code actually chooses the single most likely note at each step using an argmax.]

(根據“out”的概率，而不是隨機抽取一個值，這行程式碼實際上是在每個步驟中使用argmax選擇最可能的音符。)

# GRADED FUNCTION: music_inference_model

def music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 100):
    """
    Uses the trained "LSTM_cell" and "densor" from model() to generate a sequence of values.
    
    Arguments:
    LSTM_cell -- the trained "LSTM_cell" from model(), Keras layer object
    densor -- the trained "densor" from model(), Keras layer object
    n_values -- integer, umber of unique values
    n_a -- number of units in the LSTM_cell
    Ty -- integer, number of time steps to generate
    
    Returns:
    inference_model -- Keras model instance
    """
    
    # Define the input of your model with a shape 
    x0 = Input(shape=(1, n_values)) #(1,78)
    
    # Define s0, initial hidden state for the decoder LSTM
    a0 = Input(shape=(n_a,), name='a0') #(64,)
    c0 = Input(shape=(n_a,), name='c0') #(64,)
    a = a0
    c = c0
    x = x0

    ### START CODE HERE ###
    # Step 1: Create an empty list of "outputs" to later store your predicted values (≈1 line)
    outputs = []
    
    # Step 2: Loop over Ty and generate a value at every time step
    for t in range(Ty):
        
        # Step 2.A: Perform one step of LSTM_cell (≈1 line)
        a, _, c = LSTM_cell(x, initial_state=[a, c])
        
        # Step 2.B: Apply Dense layer to the hidden state output of the LSTM_cell (≈1 line)
        out = densor(a)

        # Step 2.C: Append the prediction "out" to "outputs". out.shape = (None, 78) (≈1 line)
        outputs.append(out)
        
        # Step 2.D: Select the next value according to "out", and set "x" to be the one-hot representation of the
        #           selected value, which will be passed as the input to LSTM_cell on the next step. We have provided 
        #           the line of code you need to do this. 
        x = Lambda(one_hot)(out) #將上一步的輸出作為下一步的輸入並將其轉換為one-hot向量
        
    # Step 3: Create model instance with the correct "inputs" and "outputs" (≈1 line)
    inference_model = Model(input=[x0, a0, c0], outputs=outputs)
    
    ### END CODE HERE ###
    
    return inference_model

Run the cell below to define your inference model. This model is hard coded to generate 50 values.

inference_model = music_inference_model(LSTM_cell, densor, n_values = 78, n_a = 64, Ty = 50)

Finally, this creates the zero-valued vectors you will use to initialize x and the LSTM state variables a and c.

x_initializer = np.zeros((1, 1, 78))
a_initializer = np.zeros((1, n_a))
c_initializer = np.zeros((1, n_a))

Exercise: Implement predict_and_sample(). This function takes many arguments including the inputs [x_initializer, a_initializer, c_initializer]. In order to predict the output corresponding to this input, you will need to carry-out 3 steps:

這個函式擁有許多的引數，其中的輸入有x_initializer,a_initializer,c_initializer. 為了使得輸出與輸入對應，需要執行下面3個步驟：

1. Use your inference model to predict an output given your set of inputs. The output pred should be a list of length $T_y$ where each element is a numpy-array of shape (1, n_values).

(1.使用inference model來預測給定的輸入，輸出應該是一個長為$T_y$的列表且每一個元素的shape為（1，n_values））

2. Convert pred into a numpy array of $T_y$ indices. Each index corresponds is computed by taking the argmax of an element of the pred list. Hint

(2.將‘pred’轉換為一個$T_y$索引的numpy陣列，每個索引對應的是通過argmax生成的列表中的最大值，即最可能的那個值。)

3. Convert the indices into their one-hot vector representations. Hint

（3.將索引轉換成one-hot向量表示）

# GRADED FUNCTION: predict_and_sample

def predict_and_sample(inference_model, x_initializer = x_initializer, a_initializer = a_initializer, 
                       c_initializer = c_initializer):
    """
    Predicts the next value of values using the inference model.
    
    Arguments:
    inference_model -- Keras model instance for inference time
    x_initializer -- numpy array of shape (1, 1, 78), one-hot vector initializing the values generation
    a_initializer -- numpy array of shape (1, n_a), initializing the hidden state of the LSTM_cell
    c_initializer -- numpy array of shape (1, n_a), initializing the cell state of the LSTM_cel
    
    Returns:
    results -- numpy-array of shape (Ty, 78), matrix of one-hot vectors representing the values generated
    indices -- numpy-array of shape (Ty, 1), matrix of indices representing the values generated
    """
    
    ### START CODE HERE ###
    # Step 1: Use your inference model to predict an output sequence given x_initializer, a_initializer and c_initializer.
    pred = inference_model.predict([x_initializer, a_initializer, c_initializer])
    # Step 2: Convert "pred" into an np.array() of indices with the maximum probabilities
    indices = np.argmax(np.array(pred),axis=-1)
    # Step 3: Convert indices to one-hot vectors, the shape of the results should be (1, )
    results = to_categorical(indices, num_classes=x_initializer.shape[-1])
    ### END CODE HERE ###
    
    return results, indices

results, indices = predict_and_sample(inference_model, x_initializer, a_initializer, c_initializer)
print("np.argmax(results[12]) =", np.argmax(results[12]))
print("np.argmax(results[17]) =", np.argmax(results[17]))
print("list(indices[1:18]) =", list(indices[1:18]))

3.3 - Generate music

Finally, you are ready to generate music. Your RNN generates a sequence of values. The following code generates music by first calling your predict_and_sample() function. These values are then post-processed into musical chords (meaning that multiple values or notes can be played at the same time).

最後，你已經準備去生成音樂了。你的RNN生成一個序列的value，下面的程式碼通過呼叫‘predict_and_sample（）’形成音樂。這些values然後處理成音樂的和絃（意味著可以同時播放多個values和符號）

Most computational music algorithms use some post-processing because it is difficult to generate music that sounds good without such post-processing. The post-processing does things such as clean up the generated audio by making sure the same sound is not repeated too many times, that two successive notes are not too far from each other in pitch, and so on. One could argue that a lot of these post-processing steps are hacks; also, a lot the music generation literature has also focused on hand-crafting post-processors, and a lot of the output quality depends on the quality of the post-processing and not just the quality of the RNN. But this post-processing does make a huge difference, so lets use it in our implementation as well.

大多數音樂計算演算法使用了一些後處理因為如果沒有後處理的話很難生成好聽的音樂。後處理確保相同的聲音不重複多次，保證兩個連續的音符在音高中彼此相距不太遠。有人可能會說，很多這些後處理步驟都是黑客行為;另外，很多音樂創作文獻也專注於手工製作後期處理器，很多輸出質量取決於後期處理的質量，而不僅僅取決於 RNN 的質量。但是這個後期處理確實有很大的不同，所以我們也可以在我們的實現中使用它。
Lets make some music!

Run the following cell to generate music and record it into your out_stream. This can take a couple of minutes.

out_stream = generate_music(inference_model)

Output：

Predicting new values for different set of chords.
Generated 51 sounds using the predicted values for the set of chords ("1") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("2") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("3") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("4") and after pruning
Generated 51 sounds using the predicted values for the set of chords ("5") and after pruning
Your generated music is saved in output/my_music.midi

To listen to your music, click File->Open… Then go to “output/” and download “my_music.midi”. Either play it on your computer with an application that can read midi files if you have one, or use one of the free online “MIDI to mp3” conversion tools to convert this to mp3.

As reference, here also is a 30sec audio clip we generated using this algorithm.

IPython.display.Audio('./data/30s_trained_model.mp3')