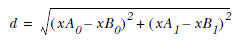k-近鄰演算法（k-Nearest Neighbors,kNN）

工作原理：

knn演算法屬於監督型別演算法。首先我們有樣本訓練集，知道每一條資料的分類。繼而，我們輸入沒有分類的新資料，將新資料的每個特徵與樣本集中的對應項進行比較，提取樣本集中最相思的資料，這樣我們可以獲得該資料的分類。一般來說，我們只選擇樣本集中前k個最相似的資料，通常k不大於20.最後，選擇k個相似資料中出現最多的分類，作為新資料的分類，此為k近鄰演算法。

優點：

精度高，對異常數值不敏感，無資料輸入假定。

缺點：計算複雜度高，空間複雜度高。無法給出任何資料的基礎結構資訊，因此我們也無法知曉平均
例項樣本和典型例項樣本具有什麼特徵

適用資料範圍：數值型，標稱型（numeric values,nominal values）

虛擬碼：

（1）計算樣本資料集中的點與當前帶分類資料的點之間的距離（計算相似程度）

（2）按照距離遞增排序

（3）選取與當前距離最小的前K個點

（4）確定k個點所在類別的出現頻率

（5）返回出現頻率最高的類別作為預測分類

python程式碼：

def createDataSet():#建立樣本訓練集
	group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
	labels = ['A','A','B','B']
	return group,labels

#intX:待分類資料（向量），dataSet,labels:樣本訓練集,k
def classi0(intX, dataSet, labels, k):
	dataSetSize = dataSet.shape[0]#訓練集大小
	diffMat = tile(intX,(dataSetSize,1)) - dataSet#把待分類資料向量複製成與訓練集等階，對應項求差
	sqDiffMat = diffMat**2#各項平方
	sqDistances = sqDiffMat.sum(axis=1)#axis=1，將一個矩陣的每一行向量相加
	distances = sqDistances**0.5#開方，求出距離
	sortedDistIndicies = distances.argsort()#從小到大排序，返回陣列的索引
	classCount = {}
	for i in range(k):#遍歷前K個樣本訓練集
		voteILabel = labels[sortedDistIndicies[i]]#對應分類
		classCount[voteILabel] = classCount.get(voteILabel,0) + 1#計數
	sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)#排序
	return sortedClassCount[0][0]#返回統計最多的分類
 

測試分類器：

錯誤率是常用的檢驗分類器的方法：

通過大量已知分類的測試資料，計算出分類器給出錯誤答案的次數除以測試的總次數。

準備資料：python獲取文字資料：

409208.3269760.953952largeDoses
144887.1534691.673904smallDoses
260521.4418710.805124didntLike

假設文字資料儲存在datingTestSet.txt文字中

def file2matrix(filename):
    fr = open(filename)
    arrayOLines = fr.readlines()#獲取所有資料，以行為單位切割
    numberOfLines = len(arrayOLines)
    returnMat = zeros((numberOfLines,3))#構建矩陣，以0填充
    classLabelVector = []
    index = 0
    for line in arrayOLines:
        line = line.strip()
        listFromLine = line.split('\t')#以tab分割為陣列
        returnMat[index,:] = listFromLine[0:3]#copy資料
        classLabelVector.append(listFromLine[-1])#儲存對應的分類
        index += 1
    return returnMat,classLabelVector
 

分析資料：

使用Matplotlib建立散點圖分析資料：

import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)#add_subplot(mnp)新增子軸、圖。subplot（m,n,p）或者subplot（mnp）此函式最常用：subplot是將多個圖畫到一個平面上的工具。其中，m表示是圖排成m行，n表示圖排成n列，也就是整個figure中有n個圖是排成一行的，一共m行，如果第一個數字是2就是表示2行圖。p是指你現在要把曲線畫到figure中哪個圖上，最後一個如果是1表示是從左到右第一個位置。
ax.scatter(datingDataMat[:,1], datingDataMat[:,2]，15.0*array(map(int,datingLabels)),15.0*array(map(int,datingLabels)))#以第二列和第三列為x,y軸畫出雜湊點，給予不同的顏色和大小
#scatter（x,y,s=1,c="g",marker="s",linewidths=0）
#s:雜湊點的大小,c:雜湊點的顏色，marker：形狀，linewidths：邊框寬度
plt.show()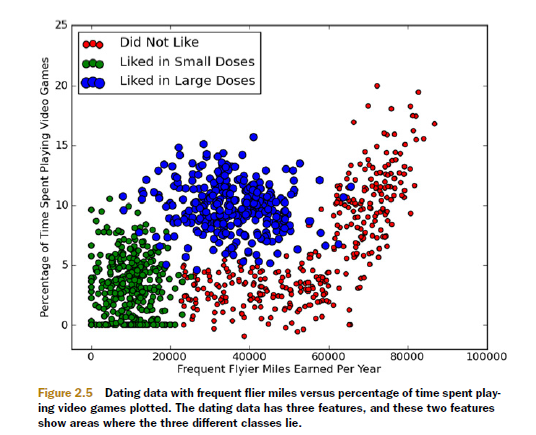

準備資料：

歸一化資料值

為了減少特徵值之間因度量不同帶來權重的偏差，需要將資料歸一化。所謂的歸一化，是講數值範圍處理在0~1或-1~1之間。

可以用如下公式：

newValue = (oldValue-min)/(max-min)

max和min分別是該項資料集特徵中的最大值和最小值。

據此可寫出歸一化函式

def autoNorm(dataSet):
    minVals = dataSet.min(0)#一維陣列，值為各項特徵（列）中的最小值
    maxVals = dataSet.max(0)
    ranges = maxVals - minVals
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m,1))
    normDataSet = normDataSet/tile(ranges, (m,1))
    return normDataSet, ranges, minVals

測試演算法：

通常只用90%的資料來訓練分類器，剩餘資料去測試分類器，獲取正確/錯誤率。

def datingClassTest():
    hoRatio = 0.10
    datingDataMat,datingLabels = file2matrix('datingTestSet.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classi0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        print "the classifier came back with: %s, the real answer is: %s" %  (classifierResult, datingLabels[i])
        if (classifierResult != datingLabels[i]): errorCount += 1.0
    print "the total error rate is: %f" % (errorCount/float(numTestVecs))

例項：數字識別系統

（1）收集資料

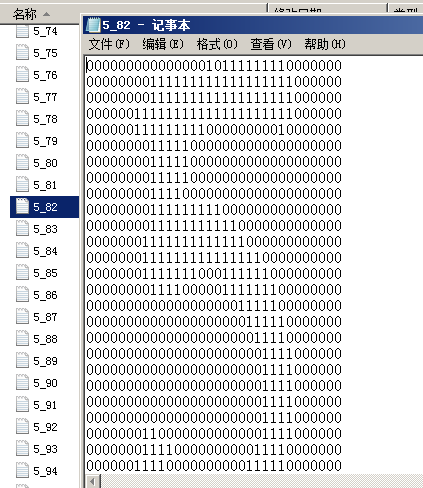
提供文字的文字檔案，大小都為32*32，每個數字大概有200個樣本

（2）準備資料，把資料轉換為上文中分類器可用的一維vector向量,從32*32變為1*24

def img2vector(filename):
	returnVect = zeros((1,1024))
	fr = open(filename)
	for i in range(32):
	lineStr = fr.readline()
	for j in range(32):
		returnVect[0,32*i+j] = int(lineStr[j])
	return returnVect

def handwritingClassTest():
	hwLabels = []
	trainingFileList = listdir('trainingDigits')#樣本資料
	m = len(trainingFileList)
	trainingMat = zeros((m,1024))
	for i in range(m):
		fileNameStr = trainingFileList[i]
		fileStr = fileNameStr.split('.')[0]
		classNumStr = int(fileStr.split('_')[0])
		hwLabels.append(classNumStr)
		trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
	testFileList = listdir('testDigits')#測試資料
	errorCount = 0.0
	mTest = len(testFileList)
	for i in range(mTest):
		fileNameStr = testFileList[i]
		fileStr = fileNameStr.split('.')[0]
		classNumStr = int(fileStr.split('_')[0])
		vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
		classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
		print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
		if (classifierResult != classNumStr): errorCount += 1.0
	print "\nthe total number of errors is: %d" % errorCount
	print "\nthe total error rate is: %f" % (errorCount/float(mTest))