機器學習實戰筆記2—決策樹
注:此係列文章裡的部分演算法和深度學習筆記系列裡的內容有重合的地方,深度學習筆記裡是看教學視訊做的筆記,此處文章是看《機器學習實戰》這本書所做的筆記,雖然演算法相同,但示例程式碼有所不同,多敲一遍沒有壞處,哈哈。(裡面用到的資料集、程式碼可以到網上搜索,很容易找到。)。Python版本3.6
機器學習十大算法系列文章:
機器學習實戰筆記1—k-近鄰演算法
機器學習實戰筆記2—決策樹
機器學習實戰筆記3—樸素貝葉斯
機器學習實戰筆記4—Logistic迴歸
機器學習實戰筆記5—支援向量機
機器學習實戰筆記6—AdaBoost
機器學習實戰筆記7—K-Means
此係列原始碼在我的GitHub裡:
一,演算法原理:
決策樹:是一種基本的分類和迴歸方法。它是基於例項特徵對例項進行分類的過程,我們可以認為決策樹就是很多if-then的規則集合。
資訊熵:夏農給出了這個公式:H=-(P1logP1+P2logP2+....) (P(X)為出現的概率),變數的不確定性越大,熵也就越大,把它弄清楚所需要的資訊量也就越大。
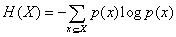
說太多文字不容易理解,看一個例子就明白了深度學習基礎課程1筆記-決策樹(Desision Tree)
二,演算法的優缺點:
優點:
1)計算複雜度不高
2)輸出結果易於理解
3)對中間值的缺失不敏感
4)可以處理不相關特徵資料
缺點:
1)可能會產生過度匹配問題
適用資料型別:數值型和標稱型
標稱型:一般在有限的資料中取,而且只存在‘是’和‘否’兩種不同的結果(一般用於分類)
數值型:可以在無限的資料中取,而且數值比較具體化,例如4.02,6.23這種值(一般用於迴歸分析)
三,例項程式碼:
1)計算資訊熵函式
#計算資訊熵 sum=-p1*logp1-p2*logp2-p3*logp3...
def calcShannonEnt(dataSet):
numEntries = len(dataSet) #資料的大小
labelCounts = {} #字典,鍵=不同的標籤,值=該標籤出現次數
for featVec in dataSet: #統計不同元素的數量及其出現次數
currentLabel = featVec[-1] #獲取最後一列類別標籤
if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 #如果字典裡沒有該類別,新建
labelCounts[currentLabel] += 1 #已有該類別,則計數加1
shannonEnt = 0.0 #資訊熵變數初始化
for key in labelCounts:
prob = float(labelCounts[key])/numEntries #計算概率
shannonEnt -= prob * log(prob,2) #log base 2
return shannonEnt輸入測試集,計算資訊熵
from math import log
#產生資料集合標籤
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers']
return dataSet, labels
dataSet, labels=createDataSet()
shannonEnt=calcShannonEnt(dataSet)
print("原資料為:",dataSet)
print("標籤為:",labels)
print("夏農熵為:",shannonEnt)計算結果為:

2)劃分資料集
'''
函式功能:按照給定特徵劃分資料集
dataSet :待劃分的資料集
axis :劃分依據的特徵所在下標
value :劃分依據的特徵
返回結果:返回axis處,所有值為value的資料集
'''
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value: #查詢特徵資料指定維度中等於value的值
#下面兩句主要功能就是剔除原資料中axis軸的特徵資料
reducedFeatVec = featVec[:axis] #取0到aixs(不包括axis)的資料
reducedFeatVec.extend(featVec[axis+1:]) #取axis+1到最後的資料
retDataSet.append(reducedFeatVec) #加入到列表中
return retDataSet
#測試
dataSet, labels = createDataSet()
print("原資料為:",dataSet)
print("標籤為:",labels)
split = splitDataSet(dataSet,0,1) #找第0維為1的資料
print("劃分後的結果為:",split)計算結果為:

找出了第0維為1的資料,返回的資料集不包含第0維資料
3)下面遍歷整個資料集,迴圈計算夏農熵和splitDataSet()函式,找到最好的劃分方式:
#選擇最好的資料集劃分方式,返回該特徵所在列
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 #最後一列用於標籤
baseEntropy = calcShannonEnt(dataSet) #計算總的資訊熵
bestInfoGain = 0.0; bestFeature = -1 #最好的資訊增益,最好的特徵
for i in range(numFeatures): #迭代所有特徵
featList = [example[i] for example in dataSet]#獲取資料集中指定列所有特徵
uniqueVals = set(featList) #保留唯一值,去掉重複的
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy #計算資訊增益; 即減少熵
if (infoGain > bestInfoGain): #將此與迄今為止的最佳收益進行比較
bestInfoGain = infoGain #如果優於當前最佳,設定為最佳
bestFeature = i
return bestFeature #返回最佳特徵所在列
#測試
dataSet, labels=createDataSet()
bestFeature=chooseBestFeatureToSplit(dataSet)
print(bestFeature)計算結果為:

說明以第0維的特徵劃分最好
4)遞迴構建決策樹
基於之前的分析,我們選取劃分結果最好的特徵劃分資料集,由於特徵很可能多與兩個,因此可能存在大於兩個分支的資料集劃分,第一次劃分之後,可以將劃分的資料繼續向下傳遞,如果將每一個劃分的資料看成是原資料集,那麼之後的每一次劃分都可以看成是和第一次劃分相同的過程,據此我們可以採用遞迴的原則處理資料集。遞迴結束的條件是:程式遍歷完所有劃分資料集的屬性,或者每個分支下的所有例項都有相同的分類。程式設計實現:
import operator
#統計各類的數量,按條件返回指定值
def majorityCnt(classList):
classCount={} #建立字典
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0 #如果該類不在字典中,則建立該類,初始值為0
classCount[vote] += 1 #對應類值加1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)#按指定維度反向排序
return sortedClassCount[0][0] #返回數最多的那類標籤
#建立樹
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet] #獲取資料集類別列表
if classList.count(classList[0]) == len(classList): #如果所有的類別都一樣
return classList[0] #返回該類別
if len(dataSet[0]) == 1: #如果資料集中只有1個數據
return majorityCnt(classList) #返回該類標籤
bestFeat = chooseBestFeatureToSplit(dataSet) #計算資訊熵最大的特徵
bestFeatLabel = labels[bestFeat] #獲取該特徵的類別標籤
myTree = {bestFeatLabel:{}} #建立樹的一個根節點
del(labels[bestFeat]) #刪除資訊熵最高的標籤
featValues = [example[bestFeat] for example in dataSet] #取出資料集中資訊熵最高的特徵
uniqueVals = set(featValues) #去除重複部分
for value in uniqueVals:
subLabels = labels[:] #複製所有標籤,因此樹木不會弄亂現有標籤
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree
#測試
dataSet, labels=createDataSet()
myTree=createTree(dataSet,labels)
print(myTree)計算結果為:

5)使用matplotlib註解繪製樹形圖
如4)我們已經從資料集中成功的建立了決策樹,但是字典的形式非常的不易於理解,因此本節採用Matplotlib庫建立樹形圖。
import matplotlib.pyplot as plt
#定義文字框和箭頭格式
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")
#獲取樹的葉子數
def getNumLeafs(myTree):
numLeafs = 0 #儲存葉子數變數
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#檢視節點是否是dictonaires,如果不是,則它們是葉節點
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
#獲取樹的深度
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#檢視節點是否是dictonaires,如果不是,則它們是葉節點
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
#繪製帶箭頭的註解
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
numLeafs = getNumLeafs(myTree) #this determines the x width of this tree
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0] #the text label for this node should be this
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes
plotTree(secondDict[key],cntrPt,str(key)) #recursion
else: #it's a leaf node print the leaf node
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
#if you do get a dictonary you know it's a tree, and the first element will be another dict
#建立樹,並顯示
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
plotTree(inTree, (0.5,1.0), '')
plt.show()
def retrieveTree(i):
listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
#測試
mytree = retrieveTree(0)
print(mytree)
createPlot(mytree)計算結果為:


6)測試演算法
在本章中,我們首先使用決策樹對實際資料進行分類,然後使用決策樹預測隱形眼鏡型別對演算法進行驗證。
(a)使用決策樹執行分類
在使用了訓練資料構造了決策樹之後,我們便可以將它用於實際資料的分類:
###決策樹的分類函式,返回當前節點的分類標籤
def classify(inputTree, featLabels, testVec): ##傳入的資料為dict型別
firstSides = list(inputTree.keys())
firstStr = firstSides[0] # 找到輸入的第一個元素
##這裡表明了python3和python2版本的差別,上述兩行程式碼在2.7中為:firstStr = inputTree.key()[0]
secondDict = inputTree[firstStr] ##建一個dict
# print(secondDict)
featIndex = featLabels.index(firstStr) # 找到在label中firstStr的下標
for i in secondDict.keys():
print(i)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]) == dict: ###判斷一個變數是否為dict,直接type就好
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel ##比較測試資料中的值和樹上的值,最後得到節點
def retrieveTree(i):
listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
# 測試
myData, labels = createDataSet()
print(labels)
mytree = retrieveTree(0)
print(mytree)
classify = classify(mytree, labels, [1, 0])
print(classify)計算結果為:

(b)使用決策樹預測隱形眼鏡型別
基於之前的分析,我們知道可以根據決策樹學習到眼科醫生是如何判斷患者需要佩戴的眼鏡片,據此我們可以幫助人們判斷需要佩戴的鏡片型別。
在此從UCI資料庫中選取隱形眼鏡資料集lenses.txt,它包含了很多患者眼部狀況的觀察條件以及醫生推薦的隱形眼鏡型別。我們選取此資料集,結合Matplotlib繪製樹形圖,進一步觀察決策樹是如何工作的,具體的程式碼如下:
fr = open('lenses.txt')
lenses = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels = ['ages','prescript','astigmatic','tearRate']
lensesTree = creatTree(lenses,lensesLabels)
print(lensesTree)
createPlot(lensesTree)計算結果為:

沿著決策樹的不同分支,我們可以得到不同患者需要佩戴的隱形眼鏡型別,從該圖中我們可以得到,只需要問四個問題就可以確定出患者需要佩戴何種隱形眼鏡。
歡迎掃碼關注我的微信公眾號

