布隆過濾器(bloom filiter) 100個隨機種子
布隆過濾器(Bloom Filter)詳解
基本概念
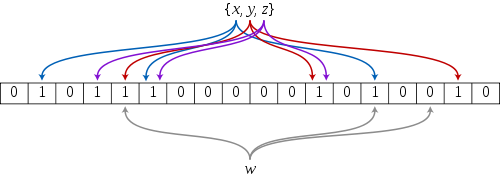
如果想判斷一個元素是不是在一個集合裡,一般想到的是將所有元素儲存起來,然後通過比較確定。連結串列,樹等等資料結構都是這種思路. 但是隨著集合中元素的增加,我們需要的儲存空間越來越大,檢索速度也越來越慢。不過世界上還有一種叫作散列表(又叫雜湊表,Hash table)的資料結構。它可以通過一個Hash函式將一個元素對映成一個位陣列(Bit Array)中的一個點。這樣一來,我們只要看看這個點是不是 1 就知道可以集合中有沒有它了。這就是布隆過濾器的基本思想。
Hash面臨的問題就是衝突。假設 Hash 函式是良好的,如果我們的位陣列長度為 m 個點,那麼如果我們想將衝突率降低到例如 1%, 這個散列表就只能容納 m/100 個元素。顯然這就不叫空間有效了(Space-efficient)。解決方法也簡單,就是使用多個 Hash,如果它們有一個說元素不在集合中,那肯定就不在。如果它們都說在,雖然也有一定可能性它們在說謊,不過直覺上判斷這種事情的概率是比較低的。
優點
相比於其它的資料結構,布隆過濾器在空間和時間方面都有巨大的優勢。布隆過濾器儲存空間和插入/查詢時間都是常數。另外, Hash 函式相互之間沒有關係,方便由硬體並行實現。布隆過濾器不需要儲存元素本身,在某些對保密要求非常嚴格的場合有優勢。
布隆過濾器可以表示全集,其它任何資料結構都不能;
k 和 m 相同,使用同一組 Hash 函式的兩個布隆過濾器的交併差運算可以使用位操作進行。
缺點
但是布隆過濾器的缺點和優點一樣明顯。誤算率(False Positive)是其中之一。隨著存入的元素數量增加,誤算率隨之增加。但是如果元素數量太少,則使用散列表足矣。
另外,一般情況下不能從布隆過濾器中刪除元素. 我們很容易想到把位列陣變成整數陣列,每插入一個元素相應的計數器加1, 這樣刪除元素時將計數器減掉就可以了。然而要保證安全的刪除元素並非如此簡單。首先我們必須保證刪除的元素的確在布隆過濾器裡面. 這一點單憑這個過濾器是無法保證的。另外計數器迴繞也會造成問題。
python 基於redis實現的bloomfilter(布隆過濾器),BloomFilter_imooc
BloomFilter_imooc下載
下載地址:https://github.com/liyaopinner/BloomFilter_imooc
依賴關係:
python 基於redis實現的bloomfilter
依賴mmh3
安裝依賴包:
pip install mmh3
bloom-filiter.py(原始碼)
