向量運算(點積,叉積)
向量加減法:
兩向量a與b的和為一個向量,記為c,即 c = a + b
c與兩向量a與b的關係遵循平行四邊形法則。
設二維向量 P =(x1,y1) , Q = (x2 , y2),則向量的加法定義為:
P+Q = (x1+x2,y1+y2)
同理,向量減法為:
P-Q = (x1-x2,y1-y2)
顯然有性質:
P+Q=Q+P P-Q=-(Q-P)
向量的點積:
兩向量a和b的點積(或稱為標積)為一個標量,記為 a·b ,它的大小為:
a · b = |a| |b| cosθ
其中,θ為兩向量a 與 b 的夾角。如果已知兩向量的點積,可以通過下公式計算出兩向量夾角,
即
θ = arccos(a · b) / (|a| |b|)
特殊情況也有a = b ,此時的θ = 0 , 有a · a = |a|²,即向量自身的點積為其模的平方。
a·a有時候也簡寫為 a²。
若設向量P= (x1,y1) , Q = (x2,y2) 則
P · Q = x1 × x2 + y1 × y2
向量的叉積:
設向量P = (x1 , y1) , Q = (x2 , y2),則向量a與向量b的叉積仍是一個向量,它的長度規定為:
|PQ| = x1y2 + x2y1
它的方向規定為:與向量P,Q 均垂直,並且使(P,Q,P×Q)成右手系,即當右手四指從a彎向b(轉角小於 Π )時,拇指的指向即使P × Q 的方向。
顯然有性質:
P×Q = -(Q*P) P ×(-Q) = -(P×Q)
叉積的作用:
叉積時一個非常重要的性質是可以通過它的符號判斷兩向量相互之間的順逆時針關係:
若P×Q > 0 , 則P在Q的順時針方向;
若P×Q < 0 , 則P在Q的逆時針方向;
若P×Q = 0 , P與Q共線,可能是同向也可能是反向;
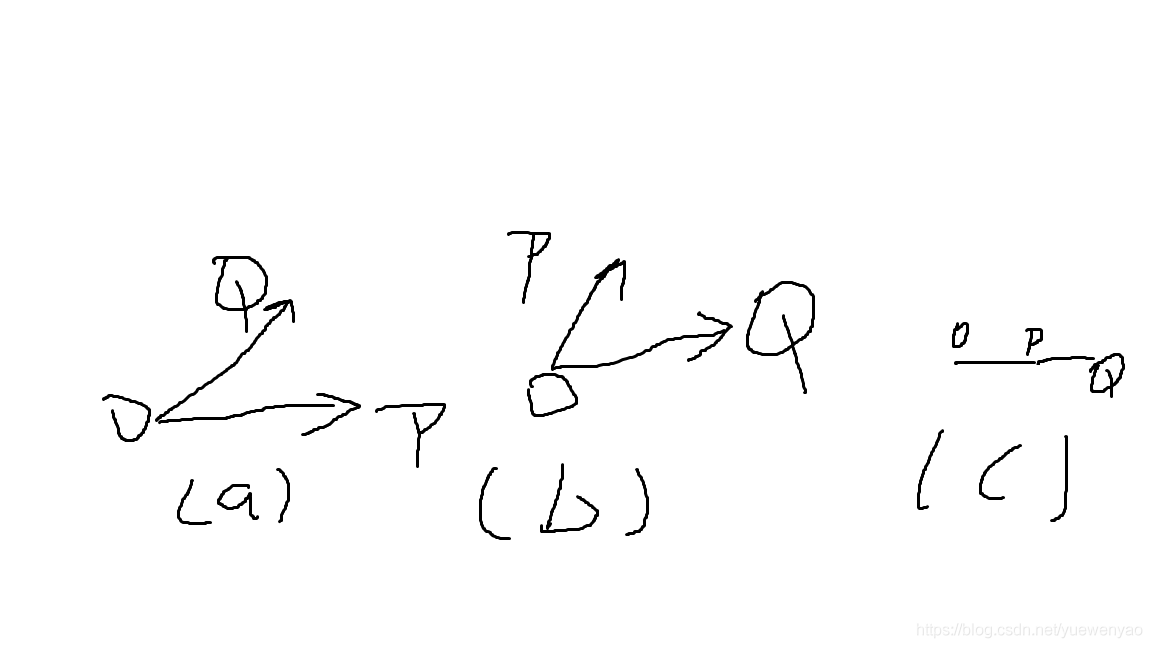
圖有點兒看著難受,先將就著看看吧。。。。。
