機器學習c12筆記:SVM學習與SVM,邏輯迴歸和kNN比較
SVM
摘自百度百科
參考書籍:機器學習實用案例解析
SVM原理
SVM方法是通過一個非線性對映p,把樣本空間對映到一個高維乃至無窮維的特徵空間中(Hilbert空間),使得在原來的樣本空間中非線性可分的問題轉化為在特徵空間中的線性可分的問題.簡單地說,就是升維和線性化.升維,就是把樣本向高維空間做對映,一般情況下這會增加計算的複雜性,甚至會引起“維數災難”,因而人們很少問津.但是作為分類、迴歸等問題來說,很可能在低維樣本空間無法線性處理的樣本集,在高維特徵空間中卻可以通過一個線性超平面實現線性劃分(或迴歸).一般的升維都會帶來計算的複雜化,SVM方法巧妙地解決了這個難題:應用核函式的展開定理,就不需要知道非線性對映的顯式表示式;由於是在高維特徵空間中建立線性學習機,所以與線性模型相比,不但幾乎不增加計算的複雜性,而且在某種程度上避免了“維數災難”.這一切要歸功於核函式的展開和計算理論.
選擇不同的核函式,可以生成不同的SVM,常用的核函式有以下4種:
1. 線性核函式K(x,y)=x·y;
2. 多項式核函式K(x,y)=[(x·y)+1]^d;
3. 徑向基函式K(x,y)=exp(-|x-y|^2/d^2)
4. 二層神經網路核函式K(x,y)=tanh(a(x·y)+b).
一般特徵
- SVM學習問題可以表示為凸優化問題,因此可以利用已知的有效演算法發現目標函式的全域性最小值。而其他分類方法(如基於規則的分類器和人工神經網路)都採用一種基於貪心學習的策略來搜尋假設空間,這種方法一般只能獲得區域性最優解。
- SVM通過最大化決策邊界的邊緣來控制模型的能力。儘管如此,使用者必須提供其他引數,如使用核函式型別和引入鬆弛變數等。
- 通過對資料中每個分類屬性引入一個啞變數,SVM可以應用於分類資料。
- SVM一般只能用在二類問題,對於多類問題效果不好。
邏輯迴歸
library('ggplot2')
# First code snippet
df <- read.csv(file.path('data', 'df.csv'))
logit.fit <- glm(Label ~ X + Y,
family = binomial(link = 'logit'),
data = df)
logit.predictions <- ifelse(predict(logit.fit) > 0 SVM分類
library('e1071')
svm.fit <- svm(Label ~ X + Y, data = df)
svm.predictions <- ifelse(predict(svm.fit) > 0, 1, 0)
mean(with(df, svm.predictions == Label))
#[1] 0.7204
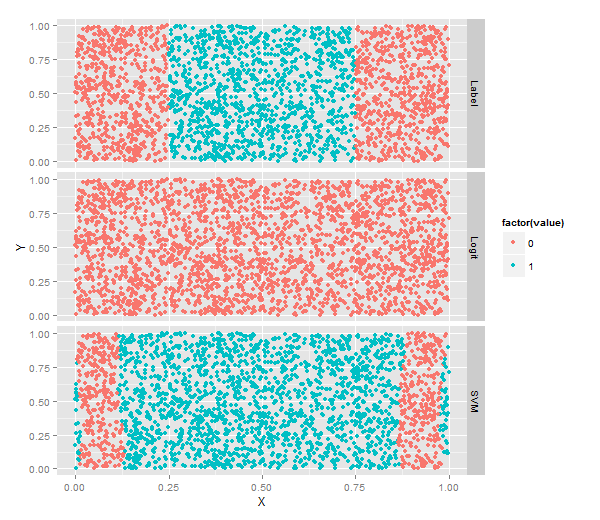
二者分類比較
# Third code snippet
library("reshape")
df <- cbind(df,
data.frame(Logit = ifelse(predict(logit.fit) > 0, 1, 0),
SVM = ifelse(predict(svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))# 將資料進行reshape!!!
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)#按照不同vareable分行畫圖!不同核方法分類結果比較
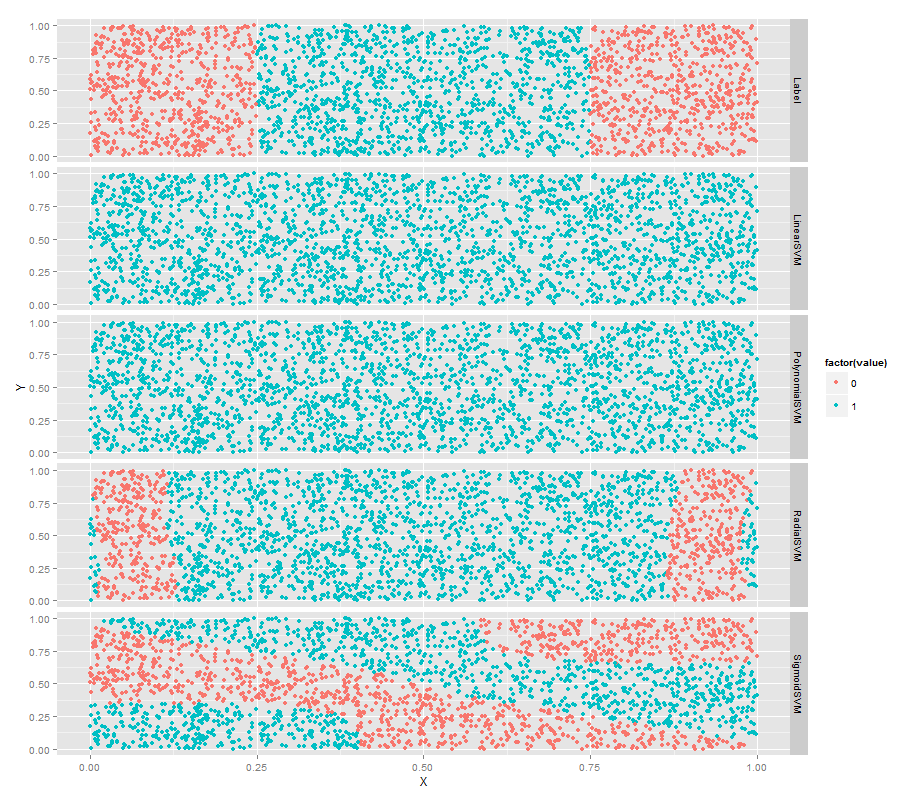
常用的核函式有以下4種:
1. 線性核函式K(x,y)=x·y;
2. 多項式核函式K(x,y)=[(x·y)+1]^d;
3. 徑向基函式K(x,y)=exp(-|x-y|^2/d^2)
4. 二層神經網路核函式K(x,y)=tanh(a(x·y)+b)(S行核函式)
# Fourth code snippet
df <- df[, c('X', 'Y', 'Label')]
linear.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'linear')
with(df, mean(Label == ifelse(predict(linear.svm.fit) > 0, 1, 0)))
polynomial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial')
with(df, mean(Label == ifelse(predict(polynomial.svm.fit) > 0, 1, 0)))
radial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial')
with(df, mean(Label == ifelse(predict(radial.svm.fit) > 0, 1, 0)))
sigmoid.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid')
with(df, mean(Label == ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
df <- cbind(df,
data.frame(LinearSVM = ifelse(predict(linear.svm.fit) > 0, 1, 0),
PolynomialSVM = ifelse(predict(polynomial.svm.fit) > 0, 1, 0),
RadialSVM = ifelse(predict(radial.svm.fit) > 0, 1, 0),
SigmoidSVM = ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)SVM的超引數設定
多項式核函式的多項式次數degree
library('ggplot2')
# First code snippet
df <- read.csv(file.path('data', 'df.csv'))
logit.fit <- glm(Label ~ X + Y,
family = binomial(link = 'logit'),
data = df)
logit.predictions <- ifelse(predict(logit.fit) > 0, 1, 0)
mean(with(df, logit.predictions == Label))
#[1] 0.5156
mean(with(df, 0 == Label))
#[1] 0.5156
# Second code snippet
library('e1071')
svm.fit <- svm(Label ~ X + Y, data = df)
svm.predictions <- ifelse(predict(svm.fit) > 0, 1, 0)
mean(with(df, svm.predictions == Label))
#[1] 0.7204
# Third code snippet
library("reshape")
df <- cbind(df,
data.frame(Logit = ifelse(predict(logit.fit) > 0, 1, 0),
SVM = ifelse(predict(svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
# Fourth code snippet
df <- df[, c('X', 'Y', 'Label')]
linear.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'linear')
with(df, mean(Label == ifelse(predict(linear.svm.fit) > 0, 1, 0)))
polynomial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial')
with(df, mean(Label == ifelse(predict(polynomial.svm.fit) > 0, 1, 0)))
radial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial')
with(df, mean(Label == ifelse(predict(radial.svm.fit) > 0, 1, 0)))
sigmoid.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid')
with(df, mean(Label == ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
df <- cbind(df,
data.frame(LinearSVM = ifelse(predict(linear.svm.fit) > 0, 1, 0),
PolynomialSVM = ifelse(predict(polynomial.svm.fit) > 0, 1, 0),
RadialSVM = ifelse(predict(radial.svm.fit) > 0, 1, 0),
SigmoidSVM = ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
# Fifth code snippet
polynomial.degree3.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 3)
with(df, mean(Label != ifelse(predict(polynomial.degree3.svm.fit) > 0, 1, 0)))
#[1] 0.5156
polynomial.degree5.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 5)
with(df, mean(Label != ifelse(predict(polynomial.degree5.svm.fit) > 0, 1, 0)))
#[1] 0.5156
polynomial.degree10.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 10)
with(df, mean(Label != ifelse(predict(polynomial.degree10.svm.fit) > 0, 1, 0)))
#[1] 0.4388
polynomial.degree12.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 12)
with(df, mean(Label != ifelse(predict(polynomial.degree12.svm.fit) > 0, 1, 0)))
#[1] 0.4464
# Sixth code snippet
df <- df[, c('X', 'Y', 'Label')]
df <- cbind(df,
data.frame(Degree3SVM = ifelse(predict(polynomial.degree3.svm.fit) > 0,
1,
0),
Degree5SVM = ifelse(predict(polynomial.degree5.svm.fit) > 0,
1,
0),
Degree10SVM = ifelse(predict(polynomial.degree10.svm.fit) > 0,
1,
0),
Degree12SVM = ifelse(predict(polynomial.degree12.svm.fit) > 0,
1,
0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)更大的degree帶來了準確率的的提升,但是,耗費的時間越來越長.最後我們在第六章進行多項式過擬合的問題又發生了.因此,在使用多項式核函式來應用svm時一定要注意交叉驗證!
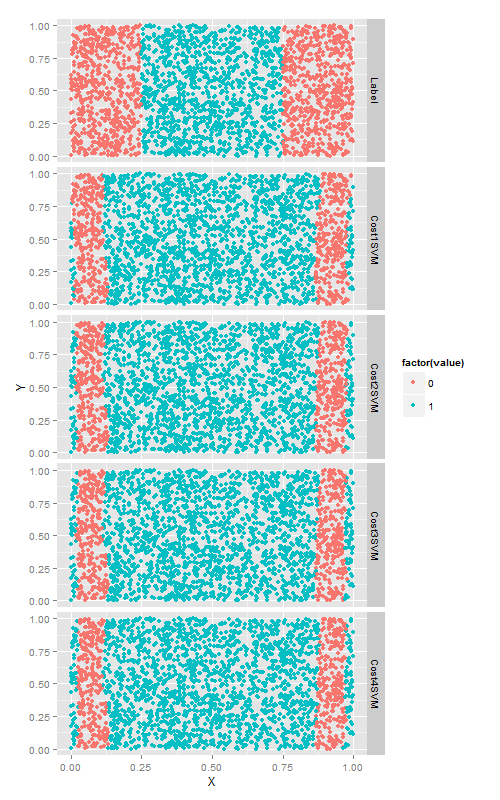
cost超引數
cost超引數他可以與任何一種SVM核函式相配合.以徑向基函式為例,嘗試4個不同的cost值,來看改變cost值帶來的變化. 這次數分類正確的點的個數.
cost引數是一個正則化超引數,就像在第六章描述的lambda引數一樣,因此增加cost只會使得模型與訓練資料擬合的更差一些.當然,正則化會使你的模型在測試集上的效果更好,因此最好使用測試集進行交叉驗證.
library('ggplot2')
# First code snippet
df <- read.csv(file.path('data', 'df.csv'))
logit.fit <- glm(Label ~ X + Y,
family = binomial(link = 'logit'),
data = df)
logit.predictions <- ifelse(predict(logit.fit) > 0, 1, 0)
mean(with(df, logit.predictions == Label))
#[1] 0.5156
mean(with(df, 0 == Label))
#[1] 0.5156
# Second code snippet
library('e1071')
svm.fit <- svm(Label ~ X + Y, data = df)
svm.predictions <- ifelse(predict(svm.fit) > 0, 1, 0)
mean(with(df, svm.predictions == Label))
#[1] 0.7204
# Third code snippet
library("reshape")
df <- cbind(df,
data.frame(Logit = ifelse(predict(logit.fit) > 0, 1, 0),
SVM = ifelse(predict(svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
# Fourth code snippet
df <- df[, c('X', 'Y', 'Label')]
linear.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'linear')
with(df, mean(Label == ifelse(predict(linear.svm.fit) > 0, 1, 0)))
polynomial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'polynomial')
with(df, mean(Label == ifelse(predict(polynomial.svm.fit) > 0, 1, 0)))
radial.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'radial')
with(df, mean(Label == ifelse(predict(radial.svm.fit) > 0, 1, 0)))
sigmoid.svm.fit <- svm(Label ~ X + Y, data = df, kernel = 'sigmoid')
with(df, mean(Label == ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
df <- cbind(df,
data.frame(LinearSVM = ifelse(predict(linear.svm.fit) > 0, 1, 0),
PolynomialSVM = ifelse(predict(polynomial.svm.fit) > 0, 1, 0),
RadialSVM = ifelse(predict(radial.svm.fit) > 0, 1, 0),
SigmoidSVM = ifelse(predict(sigmoid.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)
# Fifth code snippet
polynomial.degree3.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 3)
with(df, mean(Label != ifelse(predict(polynomial.degree3.svm.fit) > 0, 1, 0)))
#[1] 0.5156
polynomial.degree5.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 5)
with(df, mean(Label != ifelse(predict(polynomial.degree5.svm.fit) > 0, 1, 0)))
#[1] 0.5156
polynomial.degree10.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 10)
with(df, mean(Label != ifelse(predict(polynomial.degree10.svm.fit) > 0, 1, 0)))
#[1] 0.4388
polynomial.degree12.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'polynomial',
degree = 12)
with(df, mean(Label != ifelse(predict(polynomial.degree12.svm.fit) > 0, 1, 0)))
#[1] 0.4464
# Sixth code snippet
df <- df[, c('X', 'Y', 'Label')]
df <- cbind(df,
data.frame(Degree3SVM = ifelse(predict(polynomial.degree3.svm.fit) > 0,
1,
0),
Degree5SVM = ifelse(predict(polynomial.degree5.svm.fit) > 0,
1,
0),
Degree10SVM = ifelse(predict(polynomial.degree10.svm.fit) > 0,
1,
0),
Degree12SVM = ifelse(predict(polynomial.degree12.svm.fit) > 0,
1,
0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
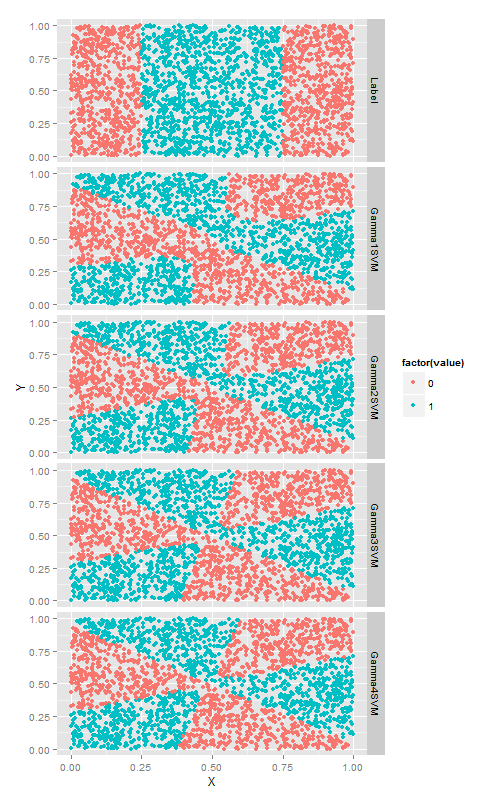
facet_grid(variable ~ .)gamma超引數
在S核函式上使用gamma, 直觀的講,改變gamma時, 由S型核函式生成的相當複雜的決策邊界會隨之彎曲變形.
# Ninth code snippet
sigmoid.gamma1.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'sigmoid',
gamma = 1)
with(df, mean(Label == ifelse(predict(sigmoid.gamma1.svm.fit) > 0, 1, 0)))
#[1] 0.478
sigmoid.gamma2.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'sigmoid',
gamma = 2)
with(df, mean(Label == ifelse(predict(sigmoid.gamma2.svm.fit) > 0, 1, 0)))
#[1] 0.4824
sigmoid.gamma3.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'sigmoid',
gamma = 3)
with(df, mean(Label == ifelse(predict(sigmoid.gamma3.svm.fit) > 0, 1, 0)))
#[1] 0.4816
sigmoid.gamma4.svm.fit <- svm(Label ~ X + Y,
data = df,
kernel = 'sigmoid',
gamma = 4)
with(df, mean(Label == ifelse(predict(sigmoid.gamma4.svm.fit) > 0, 1, 0)))
#[1] 0.4824
# Tenth code snippet
df <- df[, c('X', 'Y', 'Label')]
df <- cbind(df,
data.frame(Gamma1SVM = ifelse(predict(sigmoid.gamma1.svm.fit) > 0, 1, 0),
Gamma2SVM = ifelse(predict(sigmoid.gamma2.svm.fit) > 0, 1, 0),
Gamma3SVM = ifelse(predict(sigmoid.gamma3.svm.fit) > 0, 1, 0),
Gamma4SVM = ifelse(predict(sigmoid.gamma4.svm.fit) > 0, 1, 0)))
predictions <- melt(df, id.vars = c('X', 'Y'))
ggplot(predictions, aes(x = X, y = Y, color = factor(value))) +
geom_point() +
facet_grid(variable ~ .)演算法比較
SVM,邏輯迴歸,kNN演算法在分類中的比較.
讀取資料選取訓練測試集合
# Eleventh code snippet
load(file.path('data', 'dtm.RData'))
set.seed(1)
training.indices <- sort(sample(1:nrow(dtm), round(0.5 * nrow(dtm))))
test.indices <- which(! 1:nrow(dtm) %in% training.indices)
train.x <- dtm[training.indices, 3:ncol(dtm)]
train.y <- dtm[training.indices, 1]
test.x <- dtm[test.indices, 3:ncol(dtm)]
test.y <- dtm[test.indices, 1]
rm(dtm)邏輯迴歸
正則化的邏輯迴歸擬合
# Twelfth code snippet
library('glmnet')
regularized.logit.fit <- glmnet(train.x, train.y, family = c('binomial'))模型調優,交叉驗證
嘗試不同的lambda引數,看看哪個更好
lambdas <- regularized.logit.fit$lambda
performance <- data.frame()
for (lambda in lambdas)
{
predictions <- predict(regularized.logit.fit, test.x, s = lambda)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
performance <- rbind(performance, data.frame(Lambda = lambda, MSE = mse))
}
ggplot(performance, aes(x = Lambda, y = MSE)) +
geom_point() +
scale_x_log10()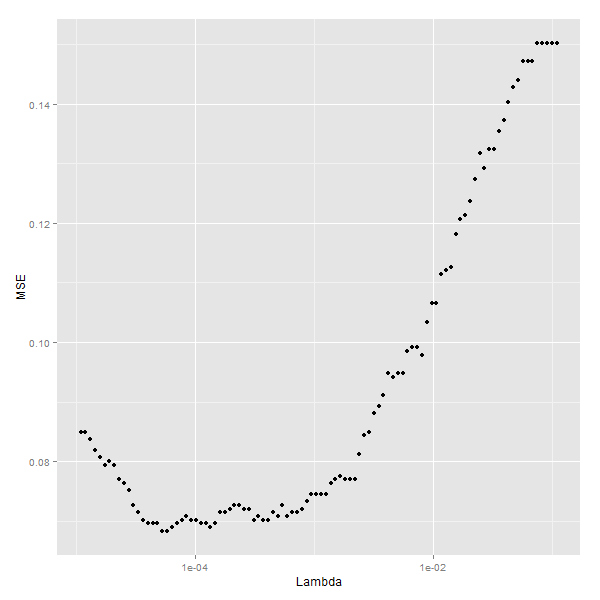
選取最下MSE下的lambda值
# Fourteenth code snippet
best.lambda <- with(performance, max(Lambda[which(MSE == min(MSE))]))
#[1] 5.788457e-05
# Fifteenth code snippet
mse <- with(subset(performance, Lambda == best.lambda), MSE)
mse
#[1] 0.06830769最優lambda值為5.788457e-05,最小的mse為[1] 5.788457e-05.
我們發現正則化的邏輯迴歸模型只有一個引數要進行調優,並且錯誤率只有6%.
SVM
這裡的SVM只用初始引數
線性核函式SVM
# Sixteenth code snippet
library('e1071')
linear.svm.fit <- svm(train.x, train.y, kernel = 'linear')
# Seventeenth code snippet
predictions <- predict(linear.svm.fit, test.x)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
mse
#0.128徑向核函式SVM
# Eighteenth code snippet
radial.svm.fit <- svm(train.x, train.y, kernel = 'radial')
predictions <- predict(radial.svm.fit, test.x)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
mse
#[1] 0.1421538我們發現徑向核函式的效果比線性的還要差,這說明解決一個問題的最優模型取決於問題資料的內在結構.本例中,徑向核函式表現不好,也許正意味著這個問題的邊界可能是線性的.而邏輯迴歸比線模型SVM好也說明這個問題.
knn
適用於非線性資料的knn也來試試看
# Nineteenth code snippet
library('class')
knn.fit <- knn(train.x, test.x, train.y, k = 50)
predictions <- as.numeric(as.character(knn.fit))
mse <- mean(predictions != test.y)
mse
#[1] 0.1396923k=5時誤差率14%, 交叉驗證看哪個k好
performance <- data.frame()
for (k in seq(5, 50, by = 5))
{
knn.fit <- knn(train.x, test.x, train.y, k = k)
predictions <- as.numeric(as.character(knn.fit))
mse <- mean(predictions != test.y)
performance <- rbind(performance, data.frame(K = k, MSE = mse))
}
best.k <- with(performance, K[which(MSE == min(MSE))])
best.mse <- with(subset(performance, K == best.k), MSE)
best.mse
#[1] 0.09169231經過調優之後knn的誤差率降到了9%,介於邏輯迴歸和svm之間.
經驗
- 對於實際資料集, 應該嘗試多個不同演算法.
- 沒有最優的演算法,最優只取決於實際問題
- 模型的效果一方面取決於真是的資料結構,另一方面也取決於你為模型的引數調優所付出的努力.