神經網路(二):Softmax函式與多元邏輯迴歸
一、 Softmax函式與多元邏輯迴歸
為了之後更深入地討論神經網路,本節將介紹在這個領域裡很重要的softmax函式,它常被用來定義神經網路的損失函式(針對分類問題)。 根據機器學習的理論,二元邏輯迴歸的模型公式可以寫為如下的形式:
在公式(1)中,對分子、分母同時乘以,得到公式(2),其中,;。
事實上,多元邏輯迴歸的模型公式也可以寫成類似的形式。具體地,假設分類問題有個類,分別記為,則多元邏輯迴歸的模型可以表示為如下的形式。
不妨記,。在公式(3)中對分子分母同時乘以,可以得到公式(4)。
公式(4)中的函式其實就是softmax函式(softmax function),記為。這個函式的輸入是一個維的行向量,而輸出也是一個維行向量,向量的每一維都在區間中,而且加總的和等於1,如圖1所示。從某種程度上來講,softmax函式與sigmoid函式非常類似,它們都能將任意的實數“壓縮”到區間。
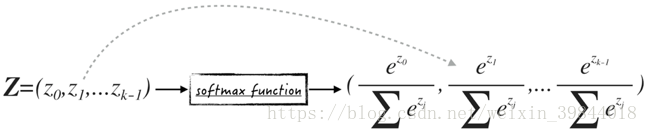
在softmax函式的基礎上,可以將邏輯迴歸轉換成圖的形式,這樣可以更直觀地在神經網路裡使用這個模型(在機器學習領域,複雜的神經網路常被表示為圖)。以二元邏輯迴歸為例,得到的影象如圖2所示。圖中的方塊表示線性模型。另外值得注意的是,圖2所表示的模型與《神經網路(一)》中的sigmoid神經元模型是一致的,只是圖2可以很輕鬆地擴充套件到多元分類問題(增加圖中方塊的數目)。
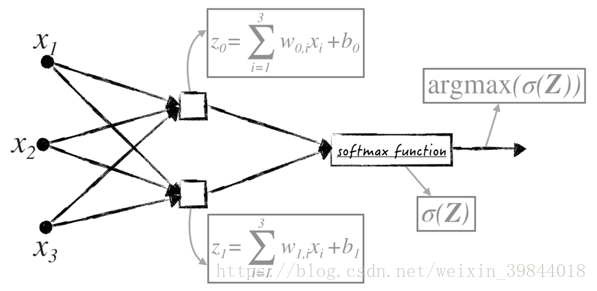
另外,藉助softmax函式,邏輯迴歸模型的損失函式可以被改寫為更簡潔的形式,如公式(5)所示。
那麼,對於元分類問題,假設第個數據的類別是,用一個維的行向量來表示它的類別[^1]:這個行向量的第個維度等於1,即,其他維度等於0,即。基於此,邏輯迴歸在這一個資料點上的損失可以寫成softmax函式與行向量矩陣乘法的形式(也可以認為是向量內積的形式),如公式(6)所示,其中
