【OpenGL ES】頂點著色器
1、輸入輸出
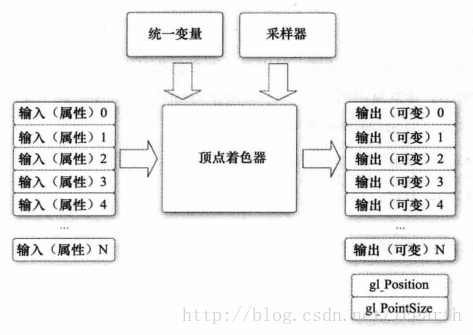
頂點著色器可用於傳統的基於頂點操作,例如通過矩陣變換位置、計算照明方程式以生成逐頂點的顏色以及生成或者變換紋理座標。頂點著色器的輸入、輸出如下圖所示。
輸入變數或屬性:用頂點陣列提供的逐頂點資料。
統一變數和統一變數緩衝區:頂點著色器使用的不變資料。
取樣器:代表頂點著色器使用的紋理的特殊統一變數型別。
著色器程式:頂點著色器程式原始碼或者描述在操作頂點的可執行檔案。
輸出或可變變數:在圖元光柵化階段,為每個生成的片段計算這些變數,並作為片段著色器的輸入傳入。
gl_Position和gl_PointSize是兩個內建變數,內建變數包括特殊變數、統一狀態以及規定最大值的常量。
內建特殊變數——
gl_VertexID:整數型輸入變數,用於儲存頂點的整數索引,精度限定符為highp。
gl_InstanceID:整數型輸入變數,用於儲存例項化繪圖呼叫中圖元的例項編號,對於常規的繪圖呼叫,該值為0,精度限定符為highp。
gl_Position:浮點型輸出變數,用於輸出頂點位置的裁剪座標,該值在裁剪和視口階段用於執行相應的圖元裁剪以及從裁剪座標到螢幕座標的頂點位置變換,頂點著色器沒有寫入gl_Position時其值是未定義的,精度限定符為highp。
glPointSize:浮點輸出變數,用於寫入以畫素表示的點尺寸,在渲染點時使用,頂點著色器輸出的這個變數值被限定在OpenGL ES 3.0實現支援的非平滑點大小範圍之內,精度限定符為highp。
glFrontFacing:特殊的布林型變數,不是由頂點著色器直接寫入的,而是根據頂點著色器生成的位置值和渲染的圖元型別生成的。
內建統一狀態——
頂點著色器有一個內建統一狀態,glDepthRange,是視窗座標中的深度範圍,型別為uniform變數,如下所示:
struct glDepthRangeParameters
{
highp float near; // near Z
highp float far; // far Z
highp float diff; // far - near
};
uniform glDepthRangeParameters glDepthRange;內建常量——
頂點著色器有如下內建常量,為每個內建常量指定的值是所有OpenGL ES 3.0實現必須支援的最小值,各種實現可能超過下面所述的最小值的常量值,實際支援的值可以通過glGetIntegerv函式查詢。
const medump int gl_MaxVertexAttribs = 16;
const medump int gl_MaxVertexUniformVectors = 256;
const medump int gl_MaxVertexOutputVectors = 16;
const medump int gl_MaxVertexTextureImageUnits = 16;
const medump int gl_MaxCombinedTextureImageUnits = 32;統一變數限制——
上面提到的gl_MaxVertexUniformVectors規定了可以用於頂點著色器的統一變數的最大數量,統一變數儲存用統一變數限定符宣告的變數、常數變數(const)、字面值以及特定於實現的常量。統一變數儲存有一定的打包規則,根據打包規則,可以確定儲存統一變數、常數變數和字面值所需的統一變數儲存總數,然後確定特定於實現的常量數量是不可能的,因為這個值不僅在不同實現中不同,而且取決於頂點著色器使用的內建著色語言函式。OpenGL ES 3.0著色語言規範規定不做任何字面值的常量傳播,也就是說同一個字面值的多個例項將被計算多次,所以在頂點著色器中儘可能避免使用字面值如0.0、1.0,應該宣告相應的常數變數代替字面值。
2、精度限定符
精度限定符用於指定任何基於浮點數或整數的變數的精度,關鍵字為lowp、mediump和highp,用法如下面的例子:
highp vec4 position;
out lowp vec4 color;
mediump float specularExp;
highp int oneConstant; 除了給每個變數指定精度限定符之外,還可以使用預設的精度限定符,而不必為每個變數單獨指定精度限定符,在頂點著色器的開始處進行宣告,如下:
presition highp float;
presition mediump int;在頂點著色器中,如果不顯式指定預設精度,float和int的預設精度都為highp。對於通常在頂點著色器中進行的操作,最可能需要的精度限定符是highp,例如用矩陣變換位置、變換法線和紋理座標或者生成紋理座標的操作都需要在highp精度下進行,顏色計算和照明方程式最可能在mediump精度下進行。
3、矩陣變換
矩陣涉及三個型別,模型矩陣將物體座標轉換為世界座標,檢視矩陣將世界矩陣轉換為眼睛座標,投影矩陣將眼睛座標轉換為裁剪座標,這三個矩陣的乘積便是模型-檢視-投影(MVP)矩陣,包括縮放、平移、旋轉等,下面是矩陣相關函式的程式碼實現。
#define PI 3.1415926535897932384626433832795f
typedef struct
{
GLfloat m[4][4];
} ESMatrix;
//
/// \brief Multiply matrix specified by result with a scaling matrix and return new matrix in result
/// \param result Specifies the input matrix. Scaled matrix is returned in result.
/// \param sx, sy, sz Scale factors along the x, y and z axes respectively
//
void esScale ( ESMatrix *result, GLfloat sx, GLfloat sy, GLfloat sz )
{
result->m[0][0] *= sx;
result->m[0][1] *= sx;
result->m[0][2] *= sx;
result->m[0][3] *= sx;
result->m[1][0] *= sy;
result->m[1][1] *= sy;
result->m[1][2] *= sy;
result->m[1][3] *= sy;
result->m[2][0] *= sz;
result->m[2][1] *= sz;
result->m[2][2] *= sz;
result->m[2][3] *= sz;
}
//
/// \brief Multiply matrix specified by result with a translation matrix and return new matrix in result
/// \param result Specifies the input matrix. Translated matrix is returned in result.
/// \param tx, ty, tz Scale factors along the x, y and z axes respectively
//
void esTranslate ( ESMatrix *result, GLfloat tx, GLfloat ty, GLfloat tz )
{
result->m[3][0] += ( result->m[0][0] * tx + result->m[1][0] * ty + result->m[2][0] * tz );
result->m[3][1] += ( result->m[0][1] * tx + result->m[1][1] * ty + result->m[2][1] * tz );
result->m[3][2] += ( result->m[0][2] * tx + result->m[1][2] * ty + result->m[2][2] * tz );
result->m[3][3] += ( result->m[0][3] * tx + result->m[1][3] * ty + result->m[2][3] * tz );
}
//
/// \brief Multiply matrix specified by result with a rotation matrix and return new matrix in result
/// \param result Specifies the input matrix. Rotated matrix is returned in result.
/// \param angle Specifies the angle of rotation, in degrees.
/// \param x, y, z Specify the x, y and z coordinates of a vector, respectively
//
void esRotate ( ESMatrix *result, GLfloat angle, GLfloat x, GLfloat y, GLfloat z )
{
GLfloat sinAngle, cosAngle;
GLfloat mag = sqrtf ( x * x + y * y + z * z );
sinAngle = sinf ( angle * PI / 180.0f );
cosAngle = cosf ( angle * PI / 180.0f );
if ( mag > 0.0f )
{
GLfloat xx, yy, zz, xy, yz, zx, xs, ys, zs;
GLfloat oneMinusCos;
ESMatrix rotMat;
x /= mag;
y /= mag;
z /= mag;
xx = x * x;
yy = y * y;
zz = z * z;
xy = x * y;
yz = y * z;
zx = z * x;
xs = x * sinAngle;
ys = y * sinAngle;
zs = z * sinAngle;
oneMinusCos = 1.0f - cosAngle;
rotMat.m[0][0] = ( oneMinusCos * xx ) + cosAngle;
rotMat.m[0][1] = ( oneMinusCos * xy ) - zs;
rotMat.m[0][2] = ( oneMinusCos * zx ) + ys;
rotMat.m[0][3] = 0.0F;
rotMat.m[1][0] = ( oneMinusCos * xy ) + zs;
rotMat.m[1][1] = ( oneMinusCos * yy ) + cosAngle;
rotMat.m[1][2] = ( oneMinusCos * yz ) - xs;
rotMat.m[1][3] = 0.0F;
rotMat.m[2][0] = ( oneMinusCos * zx ) - ys;
rotMat.m[2][1] = ( oneMinusCos * yz ) + xs;
rotMat.m[2][2] = ( oneMinusCos * zz ) + cosAngle;
rotMat.m[2][3] = 0.0F;
rotMat.m[3][0] = 0.0F;
rotMat.m[3][1] = 0.0F;
rotMat.m[3][2] = 0.0F;
rotMat.m[3][3] = 1.0F;
esMatrixMultiply ( result, &rotMat, result );
}
}
//
/// \brief Multiply matrix specified by result with a perspective matrix and return new matrix in result
/// \param result Specifies the input matrix. New matrix is returned in result.
/// \param left, right Coordinates for the left and right vertical clipping planes
/// \param bottom, top Coordinates for the bottom and top horizontal clipping planes
/// \param nearZ, farZ Distances to the near and far depth clipping planes. Both distances must be positive.
//
void esFrustum ( ESMatrix *result, float left, float right, float bottom, float top, float nearZ, float farZ )
{
float deltaX = right - left;
float deltaY = top - bottom;
float deltaZ = farZ - nearZ;
ESMatrix frust;
if ( ( nearZ <= 0.0f ) || ( farZ <= 0.0f ) ||
( deltaX <= 0.0f ) || ( deltaY <= 0.0f ) || ( deltaZ <= 0.0f ) )
{
return;
}
frust.m[0][0] = 2.0f * nearZ / deltaX;
frust.m[0][1] = frust.m[0][2] = frust.m[0][3] = 0.0f;
frust.m[1][1] = 2.0f * nearZ / deltaY;
frust.m[1][0] = frust.m[1][2] = frust.m[1][3] = 0.0f;
frust.m[2][0] = ( right + left ) / deltaX;
frust.m[2][1] = ( top + bottom ) / deltaY;
frust.m[2][2] = - ( nearZ + farZ ) / deltaZ;
frust.m[2][3] = -1.0f;
frust.m[3][2] = -2.0f * nearZ * farZ / deltaZ;
frust.m[3][0] = frust.m[3][1] = frust.m[3][3] = 0.0f;
esMatrixMultiply ( result, &frust, result );
}
//
/// \brief Multiply matrix specified by result with a perspective matrix and return new matrix in result
/// \param result Specifies the input matrix. New matrix is returned in result.
/// \param fovy Field of view y angle in degrees
/// \param aspect Aspect ratio of screen
/// \param nearZ Near plane distance
/// \param farZ Far plane distance
//
void esPerspective ( ESMatrix *result, float fovy, float aspect, float nearZ, float farZ )
{
GLfloat frustumW, frustumH;
frustumH = tanf ( fovy / 360.0f * PI ) * nearZ;
frustumW = frustumH * aspect;
esFrustum ( result, -frustumW, frustumW, -frustumH, frustumH, nearZ, farZ );
}
//
/// \brief Multiply matrix specified by result with a perspective matrix and return new matrix in result
/// \param result Specifies the input matrix. New matrix is returned in result.
/// \param left, right Coordinates for the left and right vertical clipping planes
/// \param bottom, top Coordinates for the bottom and top horizontal clipping planes
/// \param nearZ, farZ Distances to the near and far depth clipping planes. These values are negative if plane is behind the viewer
//
void esOrtho ( ESMatrix *result, float left, float right, float bottom, float top, float nearZ, float farZ )
{
float deltaX = right - left;
float deltaY = top - bottom;
float deltaZ = farZ - nearZ;
ESMatrix ortho;
if ( ( deltaX == 0.0f ) || ( deltaY == 0.0f ) || ( deltaZ == 0.0f ) )
{
return;
}
esMatrixLoadIdentity ( &ortho );
ortho.m[0][0] = 2.0f / deltaX;
ortho.m[3][0] = - ( right + left ) / deltaX;
ortho.m[1][1] = 2.0f / deltaY;
ortho.m[3][1] = - ( top + bottom ) / deltaY;
ortho.m[2][2] = -2.0f / deltaZ;
ortho.m[3][2] = - ( nearZ + farZ ) / deltaZ;
esMatrixMultiply ( result, &ortho, result );
}
//
/// \brief Perform the following operation - result matrix = srcA matrix * srcB matrix
/// \param result Returns multiplied matrix
/// \param srcA, srcB Input matrices to be multiplied
//
void esMatrixMultiply ( ESMatrix *result, ESMatrix *srcA, ESMatrix *srcB )
{
ESMatrix tmp;
int i;
for ( i = 0; i < 4; i++ )
{
tmp.m[i][0] = ( srcA->m[i][0] * srcB->m[0][0] ) +
( srcA->m[i][1] * srcB->m[1][0] ) +
( srcA->m[i][2] * srcB->m[2][0] ) +
( srcA->m[i][3] * srcB->m[3][0] ) ;
tmp.m[i][1] = ( srcA->m[i][0] * srcB->m[0][1] ) +
( srcA->m[i][1] * srcB->m[1][1] ) +
( srcA->m[i][2] * srcB->m[2][1] ) +
( srcA->m[i][3] * srcB->m[3][1] ) ;
tmp.m[i][2] = ( srcA->m[i][0] * srcB->m[0][2] ) +
( srcA->m[i][1] * srcB->m[1][2] ) +
( srcA->m[i][2] * srcB->m[2][2] ) +
( srcA->m[i][3] * srcB->m[3][2] ) ;
tmp.m[i][3] = ( srcA->m[i][0] * srcB->m[0][3] ) +
( srcA->m[i][1] * srcB->m[1][3] ) +
( srcA->m[i][2] * srcB->m[2][3] ) +
( srcA->m[i][3] * srcB->m[3][3] ) ;
}
memcpy ( result, &tmp, sizeof ( ESMatrix ) );
}
//
//// \brief Return an identity matrix
//// \param result Returns identity matrix
//
void esMatrixLoadIdentity ( ESMatrix *result )
{
memset ( result, 0x0, sizeof ( ESMatrix ) );
result->m[0][0] = 1.0f;
result->m[1][1] = 1.0f;
result->m[2][2] = 1.0f;
result->m[3][3] = 1.0f;
}
//
/// \brief Generate a transformation matrix from eye position, look at and up vectors
/// \param result Returns transformation matrix
/// \param posX, posY, posZ eye position
/// \param lookAtX, lookAtY, lookAtZ look at vector
/// \param upX, upY, upZ up vector
//
void esMatrixLookAt ( ESMatrix *result,
float posX, float posY, float posZ,
float lookAtX, float lookAtY, float lookAtZ,
float upX, float upY, float upZ )
{
float axisX[3], axisY[3], axisZ[3];
float length;
// axisZ = lookAt - pos
axisZ[0] = lookAtX - posX;
axisZ[1] = lookAtY - posY;
axisZ[2] = lookAtZ - posZ;
// normalize axisZ
length = sqrtf ( axisZ[0] * axisZ[0] + axisZ[1] * axisZ[1] + axisZ[2] * axisZ[2] );
if ( length != 0.0f )
{
axisZ[0] /= length;
axisZ[1] /= length;
axisZ[2] /= length;
}
// axisX = up X axisZ
axisX[0] = upY * axisZ[2] - upZ * axisZ[1];
axisX[1] = upZ * axisZ[0] - upX * axisZ[2];
axisX[2] = upX * axisZ[1] - upY * axisZ[0];
// normalize axisX
length = sqrtf ( axisX[0] * axisX[0] + axisX[1] * axisX[1] + axisX[2] * axisX[2] );
if ( length != 0.0f )
{
axisX[0] /= length;
axisX[1] /= length;
axisX[2] /= length;
}
// axisY = axisZ x axisX
axisY[0] = axisZ[1] * axisX[2] - axisZ[2] * axisX[1];
axisY[1] = axisZ[2] * axisX[0] - axisZ[0] * axisX[2];
axisY[2] = axisZ[0] * axisX[1] - axisZ[1] * axisX[0];
// normalize axisY
length = sqrtf ( axisY[0] * axisY[0] + axisY[1] * axisY[1] + axisY[2] * axisY[2] );
if ( length != 0.0f )
{
axisY[0] /= length;
axisY[1] /= length;
axisY[2] /= length;
}
memset ( result, 0x0, sizeof ( ESMatrix ) );
result->m[0][0] = -axisX[0];
result->m[0][1] = axisY[0];
result->m[0][2] = -axisZ[0];
result->m[1][0] = -axisX[1];
result->m[1][1] = axisY[1];
result->m[1][2] = -axisZ[1];
result->m[2][0] = -axisX[2];
result->m[2][1] = axisY[2];
result->m[2][2] = -axisZ[2];
// translate (-posX, -posY, -posZ)
result->m[3][0] = axisX[0] * posX + axisX[1] * posY + axisX[2] * posZ;
result->m[3][1] = -axisY[0] * posX - axisY[1] * posY - axisY[2] * posZ;
result->m[3][2] = axisZ[0] * posX + axisZ[1] * posY + axisZ[2] * posZ;
result->m[3][3] = 1.0f;
}4、照明
直射光——
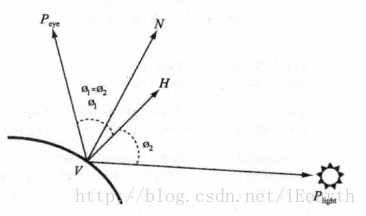
直射光照明方程式計算中的幾何因素如下圖所示。
直射光是距離場景中被照明物體無限遠處的光源,因為距離無限遠,所以光線是平行的,如太陽光。照明方向向量是一個常量,不需要逐頂點計算。在上圖中,Peye是觀看者的位置,Plight是光源的位置(w分量為0),N是法線,H是半平面向量,可以用||VPlight+VPeye||計算,即||Plight.xyz+(0,0,1)||。下面是計算直射光照明方程式的頂點著色器程式碼。
#version 300 es
struct directional_light
{
vec3 direction; // 眼睛空間內的規範化照明方向
vec3 halfplane; // 規範化的半平面向量H,對於直射光可以預先計算,因為它不會變化
vec4 ambient_color; // 環境光顏色
vec4 diffuse_color; // 漫射光顏色
vec4 specular_color; // 反射光顏色
};
struct material_properties
{
vec4 ambient_color; // 材料的環境顏色
vec4 diffuse_color; // 材料的漫射顏色
vec4 specular_color; // 材料的反射顏色
float specular_exponent; // 材料的光亮度的反光指數,用於控制反射高光的亮度
};
const float c_zero = 0.0;
const float c_one = 1.0;
uniform directional_light light;
uniform material_properties material;
// normal是一個規範化向量而且轉換到了眼睛空間
// 函式中將環境光\漫射光\反射光組合為單個顏色
// 返回計算後的顏色
// 多個光源時應該為每個光源計算一次
vec4 directional_light_color(vec3 normal)
{
vec4 computerd_color = vec4(c_zero, c_zero, c_zero, c_zero);
float ndotl; // dot product of normal & light direction
float ndoth; // dot product of normal & half-plane vector
ndotl = max(c_zero, dot(normal, light.direction);
ndoth = max(c_zero, dot(normal, light.halfplane);
computered_color += (light.ambient_color * material.ambient_color);
computered_color += (ndotl * light.diffuse_color * material.diffuse_color);
if (ndoth > c_zero) {
computered_color += (pow(ndoth, material.specular_exponent) * material.specular_color * light.specular_color);
}
return computered_color;
}聚光燈——
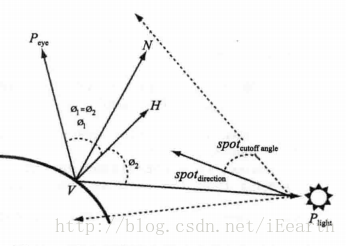
聚光燈照明方程式計算中的幾何因素如下圖所示。
聚光燈的點光源是從空間中某個位置向所有方向發出光線的光源,由位置向量(x,y,z,w)給出,其中w不等於0。點光源在各個方向上的亮度均勻,但是根據光源到物體的位置,亮度逐漸衰減,這種衰減可以用如下公式計算。
聚光燈是兼具位置和方向的光源,模擬從一個位置(Plight)以一定方向(SPOT direction)發出的光錐。光線的強度由根據與光錐中心所成的角度得出的點截止因子衰減,與光錐中軸所成的角度用VPlight與SPOT direction的點乘算出,點截止因子在SPOT direction給出的方向上為1.0,並根據SPOT cutoff angle給出的角度(弧度)按指數關係衰減為0。下面是計算聚光燈(點光源)照明方程式的頂點著色器程式碼。
#version 300 es
struct spot_light
{
vec4 position; // 在眼睛空間內的照明方向
vec4 ambient_color; // 環境光顏色
vec4 diffuse_color; // 漫射光顏色
vec4 specular_color; // 反射光顏色
vec3 spot_direction; // 規範化的點方向向量
vec3 attenuation_factors; // 距離衰減因子K0 K1 K2
bool compute_distance_attenuation; // 確定距離衰減是否必須計算
float spot_exponent; // 用於計算點截止因子的聚光燈指數
float spot_cutoff_angle; // 聚光燈截止角度(度數)
};
struct material_properties
{
vec4 ambient_color; // 材料的環境顏色
vec4 diffuse_color; // 材料的漫射顏色
vec4 specular_color; // 材料的反射顏色
float specular_exponent; // 材料的光亮度的反光指數,用於控制反射高光的亮度
};
const float c_zero = 0.0;
const float c_one = 1.0;
uniform spot_light light;
uniform material_properties material;
// normal和position在眼睛空間
// normal是一個規範化的向量
// 返回計算後的顏色
vec4 spot_light_color(vec3 normal, vec4 position)
{
vec4 computerd_color = vec4(c_zero, c_zero, c_zero, c_zero);
vec3 lightdir;
vec3 halfplane;
float ndotl;
float ndoth;
float att_factor;
att_factor = c_one;
// 假設光源位置和頂點位置的w分量相同
lightdir = light.position.xyz - position.xyz;
// 計算距離衰減因子
if (light.compute_distance_attenuation) {
vec3 att_dist;
att_dist.x = c_one;
att_dist.z = dot(lightdir, lightdir);
att_dist.y = sqrt(att_dist.z);
att_factor = c_one / dot(att_dist, light.attenuation_factors);
}
// 規範化光源方向向量
lightdir = normalize(lightdir);
// 計算點截止因子
if (light.spot_cutoff_angle < 180.0) {
float spot_factor = dot(-lightdir, light.spot_direction);
if (spot_factor >= cos(radians(light.spot_cutoff_angle))) {
spot_factor = pow(spot_factor, light.spot_exponent);
}
else {
spot_factor = c_zero;
}
// 計算距離和點衰減因子的組合
att_factor *= spot_factor;
}
if (att_factor > c_zero) {
// 根據光照公式計算光照顏色
computerd_color += (light.ambient_color * material.ambient_color);
ndotl = max(c_zero, dot(normal, lightdir);
computered_color += (ndotl * light.diffuse_color * material.diffuse_color);
halfplane = normalized(lightdir + vec3(c_zero, z_zero, c_one));
ndoth = dot(normal, halfplane);
if (ndoth > c_zero) {
computered_color += (pow(ndoth, material.specular_exponent) * material.specular_color * light.specular_color);
}
// 顏色乘以衰減因子
computerd_color *= att_factor;
}
return computered_color;
}5、生成紋理座標
下面是兩個在頂點著色器中生成紋理座標的例子,用於渲染場景中的反光物體,其中的座標將供對應的片段著色器使用,以計算反光物體的反射影象。例子中,通過生成一個反射向量,然後用這個向量計算一個紋理座標,這個座標在經緯圖(球面圖)或者立方圖(代表捕捉反射環境的6個檢視或者面,假定觀察點在反光物體的中心)中索引。固定功能OpenGL規範分別將紋理座標生成模型描述為GL_SPHERE_MAP和GL_REFLECTION_MAP,前者生成一個使用反射向量的紋理座標,以計算可以在2D紋理貼圖中查詢的2D紋理座標,後者生成的紋理座標是一個反射向量,這個向量可以用於在立方體圖中查詢的3D紋理座標。
// position is the normalized position coordinate in eye space.
// normal is the normalized normal coordinate in eye space.
// this function returns a vec2 texture coordinate.
vec2 sphere_map(vec3 position, vec3 normal)
{
reflection = reflect(position, normal);
m = 2.0 * sqrt(reflection.x * reflection.x + reflection.y * reflection.y);
return vec2(reflection.x / m + 0.5, reflection.y / m + 0.5);
}
// position is the normalized position coordinate in eye space.
// normal is the normalized normal coordinate in eye space.
// this function returns the reflection vector as a vec3 texture coordinate.
vec3 cube_map(vec3 position, vec3 normal)
{
return reflect(position, normal);
}6、頂點蒙皮
頂點蒙皮用於平滑多邊形之間的連線點,通過向每個頂點應用具有相應權重的附加變換矩陣來實現。用於頂點蒙皮的多個矩陣儲存在一個矩陣調色盤裡,每個頂點的矩陣索引引用矩陣調色盤中用於該頂點蒙皮的對應矩陣。頂點蒙皮常用於3D遊戲中的角色模型,確保它們儘可能平滑和逼真地出現而無需使用附加的幾何形狀。用於一個頂點蒙皮的矩陣數通常為2到4個,頂點蒙皮通過如下公式計算。
例如,用一個包含32個矩陣、每個頂點最多4個矩陣的矩陣調色盤生成蒙皮頂點,矩陣調色盤中的矩陣通常是4x3的列優先矩陣(每個矩陣有4個vec3專案)。如果矩陣以列優先順序儲存時,則儲存1行需要128個統一變數專案,每個專案有3個元素,上面提到的gl_MaxVertexUniformVectors最小值為256個vec4專案,所以只能儲存4行,按照統一變數打包規則,浮點值行只能儲存宣告為float型別的統一變數,這樣也就沒有空間儲存vec2、vec3或者vec4統一變數。在矩陣調色盤中,如果以行優先順序,為每個矩陣使用3個vec4專案,將能更好地儲存矩陣,這樣只會使用統一變數儲存中的96個vec4專案,剩下的160個vec4可以用於儲存其它統一變數。雖然沒有足夠的統一變數儲存來儲存計算蒙皮法線所需的逆轉置矩陣,不過,在大部分情況下,所用的矩陣都是標準正交矩陣,因此可以用於變換頂點位置和法線。
7、變換反饋
變換反饋模式允許將頂點著色器的輸出捕捉到緩衝區物件中,然後,輸出緩衝區可以作為後續繪圖呼叫中頂點資料的來源,這種方法對於在GPU上執行動畫而無需任何CPU干預的許多技術很有用,例如粒子動畫或者渲染到頂點緩衝區的物理學模擬。使用如下的glTransformFeedbackVaryings函式指定變換反饋模式期間捕捉的一組頂點屬性。
void glTransformFeedbackVaryings(GLuint program,
GLsizei count,
const char ** varyings,
GLenum bufferMode);
void glGetTransformFeedbackVarying(GLuint program,
GLuint index,
GLsizei bufSize,
GLsizei * length,
GLsizei * size,
GLenum * type,
char * name);
void glBeginTransformFeedback(GLenum primitiveMode);
void glEndTransformFeedback(void);program指定程式物件的控制代碼。count指定用於變換反饋的頂點輸出變數的數量。varyings指定一個由count個以0為結束符的字串組成的陣列,這些字串指定用於變換反饋的頂點輸出變數的名稱。bufferMode指定變換反饋啟用時用於捕捉頂點輸出變數的模式,有效值是GL_INTERLEAVED_ATTRIBS和GL_SEPARATE_ATTRIBS,前者將頂點輸出變數捕捉到單一緩衝區,後者將每個頂點輸出變數捕捉到自己的緩衝區中。呼叫glTransformFeedbackVaryings後,必須用glLinkProgram連結程式物件。然後,需要用帶GL_TRANSFORM_FEEDBACK_BUFFER的引數的glBindBuffer繫結一個或者多個緩衝區物件作為變換反饋緩衝區,該緩衝區用帶GL_TRANSFORM_FEEDBACK_BUFFER引數的glBufferData分配,用glBindBufferBase或glBindBufferRange繫結到索引繫結點。繫結變換反饋緩衝區之後,使用glBeginTransformFeedback和glEndTransformFeedback進入和退出變換反饋模式,primitiveMode指定將被捕捉到變換反饋的緩衝區物件中的圖元輸出型別,變換反饋限於非索引的GL_POINTS、GL_LINES和GL_TRANANGLES,glBeginTransformFeedback和glEndTransformFeedback之間發生的繪圖呼叫的頂點輸出將被捕捉到變換反饋緩衝區。
另外,可以在設定帶GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN引數的glBeginQuery和glEndQuery之後,用glGetObjectuiv檢索成功寫入變換反饋緩衝區物件的圖元數量。還可以在變換反饋模式中捕捉的同時用GL_RASTERIZER_QISCARD引數的glEnable和glDisable啟用和禁用光柵化,啟用GL_RASTERIZER_QISCARD時,將不會執行任何片段著色器。
8、頂點紋理
OpenGL ES 3.0支援頂點著色器中的紋理查詢操作,這在實現位移貼圖等技術時很有用,我們可以根據頂點著色器中的紋理查詢值,沿頂點法線移動頂點位置,位移貼圖技術的典型應用之一是渲染地形或者水面。在頂點著色器中執行紋理查詢有一些值得注意的限制:細節層次不是隱含計算的,不接受texture查詢函式中的偏差引數,基本紋理用於mip貼圖紋理。OpenGL ES實現支援的紋理影象單元的最大數量可以用帶GL_MAX_VERTEX_TEXTURE_UNITS引數的glGetIntegerv查詢,OpenGL ES 3.0實現可以支援的最小值是16。下面是一個執行位移貼圖的頂點著色器例子。
#version 300 es
// uniforms used by the vertex shader
uniform mat4 u_mvpMatrix; // matrix to convert P from model space to clip space
uniform sampler2D displacementMap;
// attribute inputs to the vertex shader
layout(location = 0) in vec4 a_position; // input position value
layout(location = 1) in vec3 a_normal; // input normal value
layout(location = 2) in vec2 a_texcoord; // input texcoord value
layout(location = 3) in vec4 a_color; // input color
// vertex shader output and input to the fragment shader
out vec4 v_color;
void main()
{
v_color = a_color;
float displacement = texture(displacementMap, a_texcoord).a;
vec4 displaced_position = a_position + vec4(a_normal * diplacement, 0.0);
gl_Position = u_mvpMatrix * displaced_position;
}9、例子
// Simple_VertexShader.c
typedef struct
{
// Handle to a program object
GLuint programObject;
// Uniform locations
GLint mvpLoc;
// Vertex daata
GLfloat *vertices;
GLuint *indices;
int numIndices;
// Rotation angle
GLfloat angle;
// MVP matrix
ESMatrix mvpMatrix;
} UserData;
///
// Initialize the shader and program object
//
int Init ( ESContext *esContext )
{
UserData *userData = esContext->userData;
const char vShaderStr[] =
"#version 300 es \n"
"uniform mat4 u_mvpMatrix; \n"
"layout(location = 0) in vec4 a_position; \n"
"layout(location = 1) in vec4 a_color; \n"
"out vec4 v_color; \n"
"void main() \n"
"{ \n"
" v_color = a_color; \n"
" gl_Position = u_mvpMatrix * a_position; \n"
"} \n";
const char fShaderStr[] =
"#version 300 es \n"
"precision mediump float; \n"
"in vec4 v_color; \n"
"layout(location = 0) out vec4 outColor; \n"
"void main() \n"
"{ \n"
" outColor = v_color; \n"
"} \n";
// Load the shaders and get a linked program object
userData->programObject = esLoadProgram ( vShaderStr, fShaderStr );
// Get the uniform locations
userData->mvpLoc = glGetUniformLocation ( userData->programObject, "u_mvpMatrix" );
// Generate the vertex data
userData->numIndices = esGenCube ( 1.0, &userData->vertices,
NULL, NULL, &userData->indices );
// Starting rotation angle for the cube
userData->angle = 45.0f;
glClearColor ( 1.0f, 1.0f, 1.0f, 0.0f );
return GL_TRUE;
}
///
// Update MVP matrix based on time
//
void Update ( ESContext *esContext, float deltaTime )
{
UserData *userData = esContext->userData;
ESMatrix perspective;
ESMatrix modelview;
float aspect;
// Compute a rotation angle based on time to rotate the cube
userData->angle += ( deltaTime * 40.0f );
if ( userData->angle >= 360.0f )
{
userData->angle -= 360.0f;
}
// Compute the window aspect ratio
aspect = ( GLfloat ) esContext->width / ( GLfloat ) esContext->height;
// Generate a perspective matrix with a 60 degree FOV
esMatrixLoadIdentity ( &perspective );
esPerspective ( &perspective, 60.0f, aspect, 1.0f, 20.0f );
// Generate a model view matrix to rotate/translate the cube
esMatrixLoadIdentity ( &modelview );
// Translate away from the viewer
esTranslate ( &modelview, 0.0, 0.0, -2.0 );
// Rotate the cube
esRotate ( &modelview, userData->angle, 1.0, 0.0, 1.0 );
// Compute the final MVP by multiplying the
// modevleiw and perspective matrices together
esMatrixMultiply ( &userData->mvpMatrix, &modelview, &perspective );
}
///
// Draw a triangle using the shader pair created in Init()
//
void Draw ( ESContext *esContext )
{
UserData *userData = esContext->userData;
// Set the viewport
glViewport ( 0, 0, esContext->width, esContext->height );
// Clear the color buffer
glClear ( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
// Use the program object
glUseProgram ( userData->programObject );
// Load the vertex position
glVertexAtt