遞迴演算法是把問題轉化為規模縮小了的同類問題的子問題。1）核心的子問題演算法。2）遞迴呼叫。3）給定遞迴出口。

遞迴設計使程式簡潔，也體現了設計思路在整體-區域性上結合的嚴謹，但仍不提倡程式設計使用，因為其執行效率低且佔用棧的空間問題突出。作為解決思路的一種方式還是具有魅力。

分形的自我相似，自我複製和自我巢狀用遞迴演算法來實現是合適的，事實上經典分形圖的繪製大多數可採用遞迴演算法。

一.canto三分集。

**渲染框架上有方便繪製幾何圖形的ShapeRenderer類，它和Batch畫筆都封裝了呼叫底層渲染的介面。

注：**標籤的段落無關分形演算法，是渲染框架上的一些筆記。

三分集遞迴演算法：

private void canto(int ax,int ay,int bx,int by){
		if((bx-ax)<c){
			renderer.line(ax, ay, bx, by);
		}
		else{
			int cx,cy,dx,dy;
			renderer.line(ax, ay, bx, by);
			cx=ax+(bx-ax)/3;
			cy=ay+50;
			dx=bx-(bx-ax)/3;
			dy=by+50;
			ay=ay+50;
			by=by+50;
			canto(ax,ay,cx,cy);
			canto(dx,dy,bx,by);
		}
	}
 

二.Koch妖魔曲線

演算法（修改：增加深度引數）：

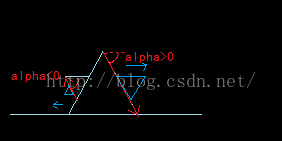
public void koch(float ax,float ay,float bx,float by,int depth){
		//delpth為深度
		if(depth<1){
			renderer.line(ax, 600-ay, bx, 600-by);
		}
		else{
			float cx,cy,dx,dy,ex,ey;
			float l,alfa;
			
			depth-=1;
			
			cx=ax+(bx-ax)/3;
			cy=ay+(by-ay)/3;
			ex=bx-(bx-ax)/3;
			ey=by-(by-ay)/3;
			
			l=(float) Math.sqrt((ex-cx)*(ex-cx)+(ey-cy)*(ey-cy));
			alfa=(float) Math.atan((ey-cy)/(ex-cx));
			
			//絕對角度在方向上的修正
			if((alfa>=0&&(ex-cx)<0)||(alfa<0&&(ex-cx)<0)){
				alfa=alfa+PI;
			}
			
			dx=(float) (cx+Math.cos(alfa+PI/3)*l);
			dy=(float) (cy+Math.sin(alfa+PI/3)*l);
			koch(ax,ay,cx,cy,depth);
			koch(ex,ey,bx,by,depth);
			koch(cx, cy, dx, dy,depth);
			koch(dx, dy, ex, ey,depth);
		}
	}
 

最終效果：

如果註釋修正絕對角度的程式碼，結果會是這樣子

妖魔曲線基本的演算法就是這樣。它的基本圖元是一條直線，在此基礎上可以修改其基本圖元為一個封閉的幾何圖形來模擬雪花。

public void kochIcing(int depth,float... vertexs){
		int length=vertexs.length;
		if(length%2!=0)
			Gdx.app.error("kochIcing", "vertexsNum must be even");
		for(int i=0;i<length-2;i+=2){
			koch(vertexs[i], vertexs[i+1],vertexs[i+2],vertexs[i+3], depth);
		}
		koch(vertexs[length-2], vertexs[length-1],vertexs[0],vertexs[1], depth);
	}

fractal.kochIcing(5, 180,120,360,432,540,120);