題目：壓縮感知測量矩陣之有限等距性質（Restricted Isometry Property,RIP）

        閱讀壓縮感知的文獻，RIP絕對是一個擡頭不見低頭見的英文簡寫，也就是有限等距性質（Restricted Isometry Property, RIP），尤其是研究測量矩陣的童鞋們，這是一個幾乎繞不開的術語，所以在測量矩陣這一塊首先討論一下RIP。

一、RIP的定義

不同文獻上表達RIP的方式不同，一般主要有以下三種：

1）王強，李佳，沈毅.壓縮感知中確定性測量矩陣構造演算法綜述[J]. 電子學報，2013，41(10)：2041-2050.（以下稱為中文定義一）

2）李樹濤，魏丹.壓縮感測綜述[J]. 自動化學報，2009，35(11)：1369-1377.（以下稱為中文定義二）

3）李坤，馬彩文，李豔，陳萍. 壓縮感知重構演算法綜述[J]. 紅外與鐳射工程，2013，42(z1)：225-232.（以下稱為中文定義三）

以上三種RIP定義中，其實前兩種是等價的。第一種定義中要注意要求x為K稀疏訊號；而第二種研究的物件矩陣是從一個矩陣中根據索引T選出其中的幾列構成的子矩陣，而並沒有對c有稀疏性的要求；也就是說你可以這樣認為，第二種中的c是第一種中的x的K個非零項，而索引T選出的幾列則是第一種中的矩陣對應x的非零項的那幾列。第三種和前面略有不同，整體上少一個平方，其實可以這樣認為，第三種中的(1±ε)的平方實際上是第一、二種中的(1±δ)，這會導致推導的引數ε和δ有差異。

下面給出很多文獻所引的參考文獻中對RIP的定義，我想應該是RIP的出處吧：

1）CandesE, Tao T. Decoding by linear programming. IEEE Transactions on InformationTheory, 2005,59(8):4203-4215. （以下稱為英文定義一）

2）CandesE. The restricted isometry property and its implications for compressedsensing[J]. Comptes Rendus Mathematique, 2008,346(8-9): 589-592. （以下稱為英文定義二）

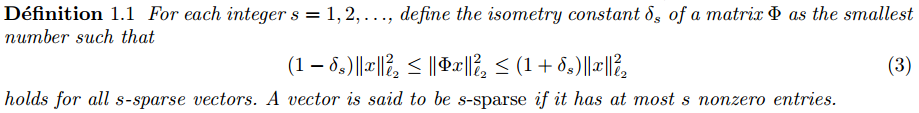
這裡的英文定義二和前面的中文定義一基本一致，英文定義一和前面的中文定義二基本一致。從這兩種定義中其實可以發現，人家是在說限制等距常數（Restricted IsometryConstant, RIC）的時候把RIP性質引出來的，RIP性質只要要求0<δ<1就可以了，而RIC是指滿足RIP的最小δ。

其實中文定義三也有對應的英文文獻，我猜是來自這篇也很火的參考文獻吧：

3）BaraniukR G. Compressive sensing. IEEE Signal Processing Magazine, 2007,24(4): 118-121.（以下稱為英文定義三）

二、RIP到底是對哪一個矩陣的約束？

RIP的定義說完了，下面說RIP性質到底是針對哪一個矩陣的？可能有人會說了，這不廢話麼，你這篇的題目不就是測量矩陣麼？因為國內外的文獻一般都是自家用自家的符號（似乎用一套自己的符號才能表明是自己的原創而不是抄襲似的，哈哈），下面呢我用一套自己的符號說一下各個矩陣的名稱以方便說明問題：

壓縮觀測y=Φx，其中y為觀測所得向量M×1，x為原訊號N×1（M<<N）。x一般不是稀疏的，但在某個變換域Ψ是稀疏的，即x=Ψθ，其中θ為K稀疏的，即θ只有K個非零項。此時y=ΦΨθ，令A=ΦΨ，則y=Aθ。

(1) y為觀測所得向量，大小為M×1

(2)x為原訊號，大小為N×1

(3)θ為K稀疏的，是訊號在x在某變換域的稀疏表示

(4) Φ稱為觀測矩陣、測量矩陣、測量基，大小為M×N

(5) Ψ稱為變換矩陣、變換基、稀疏矩陣、稀疏基、正交基字典矩陣，大小為N×N

(6)A稱為測度矩陣、感測矩陣、CS資訊運算元，大小為M×N

上式中，一般有K<<M<<N，後面三個矩陣各個文獻的叫法不一，以後我將Φ稱為測量矩陣、將Ψ稱為稀疏矩陣、將A稱為感測矩陣。

好了，符號說完了，在這裡我說實際上RIP是針對感測矩陣A的。這裡大家只要認真看一下前面的中文定義一和英文定義二就會發現裡面都要求x是稀疏的，在這我的這套符號裡面（這套符號也是從文獻中摘來的）的訊號x一般時候都不是稀疏的，所以定義中RIP針對的矩陣不是y=Φx中的Φ，而是y=Aθ中的A，定義中的x實際上是這裡的θ。

三、為何要滿足RIP性質

1、能量說

向量的2範數的平方就是訊號的能量，換成常見的公式：

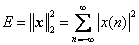
這個公式可以數字訊號處理教材中講訊號分類的章節找到，實際上將訊號看成是電壓訊號或電流訊號，這是在單位電阻上的能量（即u²t/R或i²t/R，R=1Ω，再離散即可）。

這裡將中文定義一中的RIP性質的不等式按剛才規定好的一套符號重新寫出：

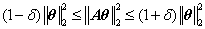
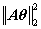
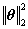
這裡的實際上是 ，即輸出訊號的能量， 即輸入訊號的能量（稀疏變換x=Ψθ為正交變換，而正交變換保持能量不變，即訊號理論中的Parseval定理）。

1）沙威. “壓縮感測”引論.http://www.eee.hku.hk/~wsha/Freecode/Files/Compressive_Sensing.pdf

RIP其實可以看成刻畫一個矩陣和標準正交陣的相似程度。其對於向量做變化後的 L2 能量（範數平方）相較於原向量的能量的變化不超過RIP。RIP對於Stability 的分析非常有效。RIP 是由Candes 和Tao 提出來的，可以看他們的提出這個概念的文章: Decoding by LinearProgramming（注：此段話在評論部分）

其實取極限當δ=0時（RIP要求0<δ<1），RIP的不等式實際上表示的是觀測所得向量y的能量等於訊號x的能量，線上性代數中所講的正交變換也具有這種性質，也稱為等距變換（把訊號將為二維或三維時2範數的平方可形象的理解為到原點的距離），當然這裡的變換因為感測矩陣A不可能是正交矩陣（不是方陣），但當極限δ=0時也能保持能量相等（也可以稱為等距吧），而RIP要求0<δ<1，所以不可能等距，所以就稱為有限等距性質吧。（從其它地方見過類似的解釋，加上個人的理解，不知是否妥當）

2、唯一對映說

個人感覺這種說法還是比較好理解的。

RIP性質（有限等距性質）保證了觀測矩陣不會把兩個不同的K稀疏訊號對映到同一個集合中（保證原空間到稀疏空間的一一對映關係），要求從觀測矩陣中抽取的每M個列向量構成的矩陣是非奇異的。

2）Candes E. Therestricted isometry property and its implications for compressed sensing[J].Comptes Rendus Mathematique, 2008,346(8-9): 589-592.

3）Candes E, Tao T.Decoding by linear programming. IEEE Transactions on Information Theory,2005,59(8):4203-4215.

從(2)中可以看出，當δ_2s<1時可以保證零範數問題有唯一的稀疏解，而當δ_2s<sqrt(2)-1時則可以保證零範數和1範數等價（零範數求解為NP-hard問題，在此前提下將其轉化為1範數求最優化問題，這時是個凸優化，轉化為凸優化後有很多好處，參見壓縮感知中的數學知識：凸優化）。

從(3)中可以看出，當δ_2s<1時可以保證(P0)有唯一解，並且用反證法對此問題進行了證明，大概思路是假設有兩個解，會發現從RIP性質的不等式中可以得出這兩個解是相等的。

四、其它

文獻[李樹濤，魏丹.壓縮感測綜述[J]. 自動化學報，2009，35(11)：1369-1377.]中提到：

其中這裡提到的文獻[4]即為文獻[BaraniukR G. Compressive sensing. IEEE Signal Processing Magazine, 2007,24(4):118-121.]，這裡解答了一個問題：“由於稀疏矩陣是固定的，要使得感測矩陣滿足約束等距條件，可以通過設計測量矩陣解決”，本文第二部分明確說了RIP是針對感測矩陣的，但為什麼我們確來研究測量矩陣呢？我想這就是答案了吧。這裡還提到了“2K列都不相關”，其實這很好理解：如果矩陣有2K列線性相關，則對於某一個2K稀疏的訊號必然會有Aθ_2K=0，又因為一個2K稀疏的訊號可以寫成兩個K稀疏的訊號相減（把2K稀疏訊號的2K個非零項分成兩部分，每部分分別包含K個非零項，其餘部分填零長度與原2K稀疏訊號保持不變，即得到了兩個K稀疏訊號，其中的一個K稀疏訊號中的K個非零項乘負一，另一部分減這一部分必然等於2K稀疏訊號），因此有A(θ_K1－θ_K2)=0，即Aθ_K1=Aθ_K2，也就是說對於兩個不同的K稀疏訊號θ_K1和θ_K2，壓縮觀測後得到了同一個y，即不能保證唯一對映，所以矩陣不能有2K列線性相關，否則將不能保證唯一對映。

五、結語

總結一下RIP性質：

矩陣滿足2K階RIP保證了能夠把任意一個K稀疏訊號θ_K對映為唯一的y，也就是說要想通過壓縮觀測y恢復K稀疏訊號θ_K，必須保證感測矩陣滿足2K階RIP，滿足2K階RIP的矩陣任意2K列線性無關。

列不相關感覺實際上應該是測量矩陣的另一個引數：spark引數，這個在這裡就不說了，下一篇再聊聊吧……

最後提兩個疑問：

從能量角度來說，RIP實際上保證了壓縮觀測前後的能量變化範圍，下限不能為零，上限不能超過原訊號的兩倍（RIP不等式中取δ=1的極限時）。這裡的下限不能為零是很好理解的，當訊號能量為零時表示原訊號的所有項全部為零，零向量中自然是沒有資訊的；上限怎麼理解呢？為什麼壓縮觀測後的能量不能超過原訊號的兩倍呢？

另外，有限等距常數RIC的取範圍定義中約束為大於0小於1，RIC越趨近於零則壓縮觀測前後能量變化越小，是不是可以這樣說：RIC越小說明對矩陣的要求越嚴（能量變化範圍小），RIC越大說明對矩陣要求越寬鬆。比如在證明1範數與0範數問題等價時經常說把δ的範圍放寬到某個值（δ範圍變大），是不是這麼個理呢？