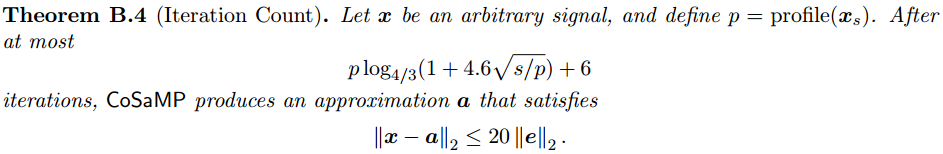題目：壓縮感知重構演算法之壓縮取樣匹配追蹤（CoSaMP）

壓縮取樣匹配追蹤(CompressiveSampling MP)是D. Needell繼ROMP之後提出的又一個具有較大影響力的重構演算法。CoSaMP也是對OMP的一種改進，每次迭代選擇多個原子，除了原子的選擇標準之外，它有一點不同於ROMP：ROMP每次迭代已經選擇的原子會一直保留，而CoSaMP每次迭代選擇的原子在下次迭代中可能會被拋棄。

0、符號說明如下：

        壓縮觀測y=Φx，其中y為觀測所得向量M×1，x為原訊號N×1（M<<N）。x一般不是稀疏的，但在某個變換域Ψ是稀疏的，即x=Ψθ，其中θ為K稀疏的，即θ

        (1) y為觀測所得向量，大小為M×1

        (2)x為原訊號，大小為N×1

        (3)θ為K稀疏的，是訊號在x在某變換域的稀疏表示

        (4) Φ稱為觀測矩陣、測量矩陣、測量基，大小為M×N

        (5) Ψ稱為變換矩陣、變換基、稀疏矩陣、稀疏基、正交基字典矩陣，大小為N×N

        (6)A稱為測度矩陣、感測矩陣、CS資訊運算元，大小為M×N

上式中，一般有K<<M<<N，後面三個矩陣各個文獻的叫法不一，以後我將Φ稱為測量矩陣、將Ψ稱為稀疏矩陣

        注意：這裡的稀疏表示模型為x=Ψθ，所以感測矩陣A=ΦΨ；而有些文獻中稀疏模型為θ=Ψx，而一般Ψ為Hermite矩陣(實矩陣時稱為正交矩陣)，所以Ψ^-1=Ψ^H (實矩陣時為Ψ^-1=Ψ^T)，即x=Ψ^Hθ，所以感測矩陣A=ΦΨ^H，例如沙威的OMP例程中就是如此。

1、CoSaMP重構演算法流程：

2、壓縮取樣匹配追蹤(CoSaOMP)Matlab程式碼(CS_CoSaMP.m)

        程式碼參考了文獻[5]中的Demo_CS_CoSaMP.m，也可參考文獻[6]，或者文獻[7]中的cosamp.m。值得一提的是文獻[5]的所有程式碼都挺不錯的，從程式碼註釋中可以得知作者是ustc的ChengfuHuo，百度一下可知是中國科技大學的霍承富博士，已於2012年6月畢業，博士論文題目是《超光譜遙感影象壓縮技術研究》，向這位學長致敬！（雖然不是一個學校的）

        2015-05-13更新：

function [ theta ] = CS_CoSaMP( y,A,K )
%CS_CoSaOMP Summary of this function goes here
%Created by [email protected]@2015-04-29
%Version: 1.1 modified by jbb0523 @2015-05-09
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%	y = Phi*Psi * theta
%   令 A = Phi*Psi, 則y=A*theta
%   K is the sparsity level
%   現在已知y和A，求theta
%   Reference:Needell D，Tropp J A．CoSaMP：Iterative signal recovery from
%   incomplete and inaccurate samples[J]．Applied and Computation Harmonic 
%   Analysis，2009，26：301-321.
    [y_rows,y_columns] = size(y);
    if y_rows<y_columns
        y = y';%y should be a column vector
    end
    [M,N] = size(A);%感測矩陣A為M*N矩陣
    theta = zeros(N,1);%用來儲存恢復的theta(列向量)
    Pos_theta = [];%用來迭代過程中儲存A被選擇的列序號
    r_n = y;%初始化殘差(residual)為y
    for kk=1:K%最多迭代K次
        %(1) Identification
        product = A'*r_n;%感測矩陣A各列與殘差的內積
        [val,pos]=sort(abs(product),'descend');
        Js = pos(1:2*K);%選出內積值最大的2K列
        %(2) Support Merger
        Is = union(Pos_theta,Js);%Pos_theta與Js並集
        %(3) Estimation
        %At的行數要大於列數，此為最小二乘的基礎(列線性無關)
        if length(Is)<=M
            At = A(:,Is);%將A的這幾列組成矩陣At
        else%At的列數大於行數，列必為線性相關的,At'*At將不可逆
            if kk == 1
                theta_ls = 0;
            end
            break;%跳出for迴圈
        end
        %y=At*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
        %(4) Pruning
        [val,pos]=sort(abs(theta_ls),'descend');
        %(5) Sample Update
        Pos_theta = Is(pos(1:K));
        theta_ls = theta_ls(pos(1:K));
        %At(:,pos(1:K))*theta_ls是y在At(:,pos(1:K))列空間上的正交投影
        r_n = y - At(:,pos(1:K))*theta_ls;%更新殘差 
        if norm(r_n)<1e-6%Repeat the steps until r=0
            break;%跳出for迴圈
        end
    end
    theta(Pos_theta)=theta_ls;%恢復出的theta
end

function [ theta ] = CS_CoSaMP( y,A,K )
%CS_CoSaMP Summary of this function goes here
%Version: 1.0 written by jbb0523 @2015-04-29
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%	y = Phi*Psi * theta
%   令 A = Phi*Psi, 則y=A*theta
%   K is the sparsity level
%   現在已知y和A，求theta
%   Reference:Needell D，Tropp J A．CoSaMP：Iterative signal recovery from
%   incomplete and inaccurate samples[J]．Applied and Computation Harmonic 
%   Analysis，2009，26：301-321.
    [y_rows,y_columns] = size(y);
    if y_rows<y_columns
        y = y';%y should be a column vector
    end
    [M,N] = size(A);%感測矩陣A為M*N矩陣
    theta = zeros(N,1);%用來儲存恢復的theta(列向量)
    Pos_theta = [];%用來迭代過程中儲存A被選擇的列序號
    r_n = y;%初始化殘差(residual)為y
    for kk=1:K%最多迭代K次
        %(1) Identification
        product = A'*r_n;%感測矩陣A各列與殘差的內積
        [val,pos]=sort(abs(product),'descend');
        Js = pos(1:2*K);%選出內積值最大的2K列
        %(2) Support Merger
        Is = union(Pos_theta,Js);%Pos_theta與Js並集
        %(3) Estimation
        %At的行數要大於列數，此為最小二乘的基礎(列線性無關)
        if length(Is)<=M
            At = A(:,Is);%將A的這幾列組成矩陣At
        else%At的列數大於行數，列必為線性相關的,At'*At將不可逆
            break;%跳出for迴圈
        end
        %y=At*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At'*At)^(-1)*At'*y;%最小二乘解
        %(4) Pruning
        [val,pos]=sort(abs(theta_ls),'descend');
        %(5) Sample Update
        Pos_theta = Is(pos(1:K));
        theta_ls = theta_ls(pos(1:K));
        %At(:,pos(1:K))*theta_ls是y在At(:,pos(1:K))列空間上的正交投影
        r_n = y - At(:,pos(1:K))*theta_ls;%更新殘差 
        if norm(r_n)<1e-6%Repeat the steps until r=0
            break;%跳出for迴圈
        end
    end
    theta(Pos_theta)=theta_ls;%恢復出的theta
end

        在程式主迴圈的(3)Estimation部分增加了以下幾行程式碼，以使函式執行更加穩定：

            if kk == 1
                theta_ls = 0;
            end

3、CoSaMP單次重構測試程式碼

        以下測試程式碼基本與OMP單次重構測試程式碼一樣。

%壓縮感知重構演算法測試
clear all;close all;clc;
M = 64;%觀測值個數
N = 256;%訊號x的長度
K = 12;%訊號x的稀疏度
Index_K = randperm(N);
x = zeros(N,1);
x(Index_K(1:K)) = 5*randn(K,1);%x為K稀疏的，且位置是隨機的
Psi = eye(N);%x本身是稀疏的，定義稀疏矩陣為單位陣x=Psi*theta
Phi = randn(M,N);%測量矩陣為高斯矩陣
A = Phi * Psi;%感測矩陣
y = Phi * x;%得到觀測向量y
%% 恢復重構訊號x
tic
theta = CS_CoSaMP( y,A,K );
x_r = Psi * theta;% x=Psi * theta
toc
%% 繪圖
figure;
plot(x_r,'k.-');%繪出x的恢復訊號
hold on;
plot(x,'r');%繪出原訊號x
hold off;
legend('Recovery','Original')
fprintf('\n恢復殘差：');
norm(x_r-x)%恢復殘差

        執行結果如下：（訊號為隨機生成，所以每次結果均不一樣）

        1）圖：

        2）Command  windows

        Elapsedtime is 0.073375 seconds.

        恢復殘差：

        ans=

          7.3248e-015

4、測量數M與重構成功概率關係曲線繪製例程程式碼

clear all;close all;clc;
%% 引數配置初始化
CNT = 1000;%對於每組(K,M,N)，重複迭代次數
N = 256;%訊號x的長度
Psi = eye(N);%x本身是稀疏的，定義稀疏矩陣為單位陣x=Psi*theta
K_set = [4,12,20,28,36];%訊號x的稀疏度集合
Percentage = zeros(length(K_set),N);%儲存恢復成功概率
%% 主迴圈，遍歷每組(K,M,N)
tic
for kk = 1:length(K_set)
    K = K_set(kk);%本次稀疏度
    M_set = 2*K:5:N;%M沒必要全部遍歷，每隔5測試一個就可以了
    PercentageK = zeros(1,length(M_set));%儲存此稀疏度K下不同M的恢復成功概率
    for mm = 1:length(M_set)
       M = M_set(mm);%本次觀測值個數
       fprintf('K=%d,M=%d\n',K,M);
       P = 0;
       for cnt = 1:CNT %每個觀測值個數均執行CNT次
            Index_K = randperm(N);
            x = zeros(N,1);
            x(Index_K(1:K)) = 5*randn(K,1);%x為K稀疏的，且位置是隨機的                
            Phi = randn(M,N)/sqrt(M);%測量矩陣為高斯矩陣
            A = Phi * Psi;%感測矩陣
            y = Phi * x;%得到觀測向量y
            theta = CS_CoSaMP(y,A,K);%恢復重構訊號theta
            x_r = Psi * theta;% x=Psi * theta
            if norm(x_r-x)<1e-6%如果殘差小於1e-6則認為恢復成功
                P = P + 1;
            end
       end
       PercentageK(mm) = P/CNT*100;%計算恢復概率
    end
    Percentage(kk,1:length(M_set)) = PercentageK;
end
toc
save CoSaMPMtoPercentage1000 %執行一次不容易，把變數全部儲存下來
%% 繪圖
S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
for kk = 1:length(K_set)
    K = K_set(kk);
    M_set = 2*K:5:N;
    L_Mset = length(M_set);
    plot(M_set,Percentage(kk,1:L_Mset),S(kk,:));%繪出x的恢復訊號
    hold on;
end

        本程式在聯想ThinkPadE430C筆記本（4GBDDR3記憶體，i5-3210）上執行共耗時1102.325890秒，程式中將所有資料均通過“save CoSaMPMtoPercentage1000”儲存了下來，以後可以再對資料進行分析，只需“load CoSaMPMtoPercentage1000”即可。

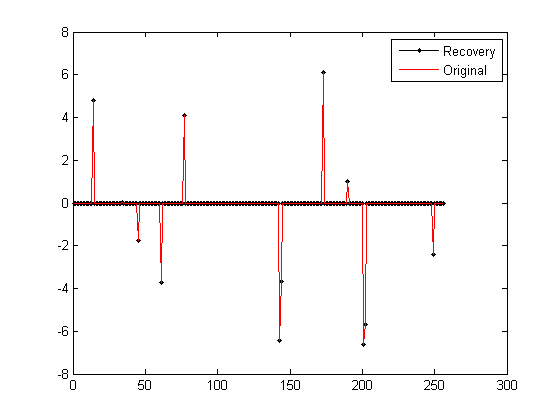
        本程式執行結果：

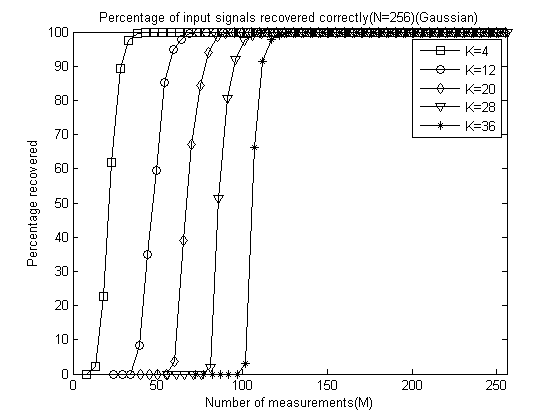
5、結語

        有關CoSaMP的原始引用文獻共有四個版本，分別如參考文獻[1][2][3][4]，可依據連結下載，其中[1]和[2]基本一致，本人主要看的是文獻[2]。

        有關CoSaMP的演算法流程，可參見參考文獻[2]：

這個流程中的其它部分都可以看懂，就是那句“b|Tc←0”很不明白，“Tc”到底是指的什麼呢？現在看來應該是T的補集(complementary set)，向量b的元素序號為全集，子集T對應的元素等於最小二乘解，補集對應的元素為零。

        有關演算法流程中的“注3”提到的迭代次數，在文獻[2]中多處有提及，不過面向的問題不同，可以文獻[2]中搜索“Iteration Count”，以下給出三處：

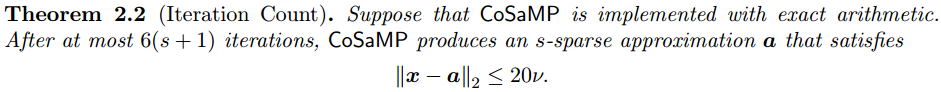
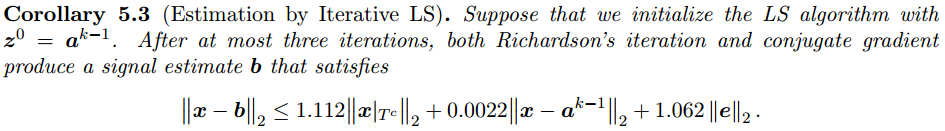
        文獻[8]的3.4節提到“設演算法的迭代步長為K，候選集中最多有3K個原子，每次最多剔除K個原子，以保證支撐集中有2K個原子”，對這個觀點我保留意見，我認為應該是“每次最多剔除2K個原子，以保證支撐集中有K個原子”。

參考文獻：

[1]D. Needell, J.A. Tropp, CoSaMP: Iterative signal recovery from incomplete andinaccurate samples, ACM Technical Report 2008-01, California Institute ofTechnology, Pasadena, 2008.

(http://authors.library.caltech.edu/27169/)

[2]D. Needell, J.A. Tropp．CoSaMP: Iterative signal recoveryfrom incomplete and inaccurate samples.http://arxiv.org/pdf/0803.2392v2.pdf

[3] D. Needell, J.A. Tropp．CoSaMP：Iterativesignal recovery from incomplete and inaccurate samples[J]．Appliedand Computation Harmonic Analysis，2009，26：301-321.

(http://www.sciencedirect.com/science/article/pii/S1063520308000638)

[4]D.Needell, J.A. Tropp．CoSaMP: Iterative signal recoveryfrom incomplete and inaccurate samples[J]. Communications of theACM，2010，53(12)：93-100.

(http://dl.acm.org/citation.cfm?id=1859229)

[5]Li Zeng. CS_Reconstruction.http://www.pudn.com/downloads518/sourcecode/math/detail2151378.html

[6]wanghui.csmp. http://www.pudn.com/downloads252/sourcecode/others/detail1168584.html

[7]付自傑.cs_matlab. http://www.pudn.com/downloads641/sourcecode/math/detail2595379.html

[8]楊真真，楊震，孫林慧.訊號壓縮重構的正交匹配追蹤類演算法綜述[J]. 訊號處理，2013，29(4)：486-496.