F=（λ1F1+…λmFm）/(λ1+…λm)

=W1F1+…WmFm

9.得分排序

--------------------------------------------------------------------------------------------------------------------------------------

想直接看結果的上面就是，沒什麼，下面就是我個人認為重要的，想學好因子分析要知道。

因子分析模型，又名正交因子模型

X=AF+ɛ

其中：

X=[X1,X2,X3...XP]‘

A=

F=[F1,F2...Fm]'

ɛ=[ɛ1,ɛ2...ɛp]'

以上滿足：

（1）m小於等於p

（2）cov(F,ɛ)=0

(3)Var(F)=Im

D(ɛ)=Var(ɛ)=

ɛ1,ɛ2...ɛp不相關，且方差不同

我們把F成為X公共因子，A為荷載矩陣，ɛ為X特殊因子

A=(aij)

數學上證明：aij就是i個變數與第j個因子的相關係數，參見層次分析法aij定義。

<1>荷載矩陣

就荷載矩陣的估計和解釋方法有主因子和極大似然估計，我們就主因子分析而言：（是主因子不是主成份）

設隨機向量X的協方差陣為Ʃ

λ1,λ2,λ3..>0為Ʃ的特徵根

μ1，μ2，μ3...為對應的標準正交向量

我們大一學過線代或者高代，裡面有個東西叫譜分析：

Ʃ=λ1μ1μ1’+......+λpμpμp’

=

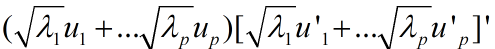
當因子個數和變數個數一樣多，特殊因子方差為0.

此時，模型為X=AF,其中Var(F)=Ip

於是，Var(X)=Var(AF)=AVar(F)A'=AA'

對照Ʃ分解式,A第j列應該是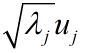也就是說，除了uj前面部分，第j列因子簽好為第j個主成份的係數，所以為主成份法。

如果非要作死考慮ɛ

原來的協方差陣可以分解為：

Ʃ=AA'+D=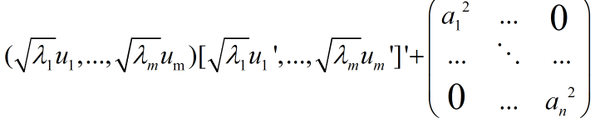以上分析的目的；

1.因子分析模型是描述原變數X的協方差陣Ʃ的一種模型

2.主成份分析中每個主成份相應係數是唯一確定的，然而因子分析中的每個因子的相應係數不是唯一的，因而我們的因子荷載矩陣不是唯一的

(主成分分析是因子分析的特例，非常類似，有興趣的可以去看看，這兩者非常容易混淆)

<2>共同度和方差貢獻

無論是在spss或者R的因子分析中都圍繞著貢獻度，我們來看下，它到底是什麼意思。

由因子分析模型，當僅有一個公因子F時，

Var(Xi)=Var(aiF)+Var(ɛi)

由於資料標準化，左端為1，右端分別為共性方差和個性方差

共性方差越大，說明共性因子作用越大。

因子載荷矩陣A中的第i行元素之平方和記為hi2

成為變數(Xi)共同度

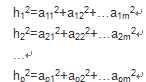它是公共因子對(Xi)的方差鎖做出的貢獻，反映了全部公共因子對變數(Xi)的影響。

hi2大表明第i個分量對F的每一個分量F1,F2,...Fm的共同依賴程度大

將因子載荷矩陣A的第j列的各元素的平方和記為gj2

成為公共因子Fj對x的方差貢獻。

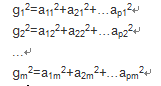gj2表示第j個公共因子Fj對x的每一個分量Xi所提供的方差的總和，他就是衡量公共因子的相對重要行的指標。gj2越大，表明公共因子Fj對x的貢獻越大，或者說對x的影響和作用就越大。

如果將載荷矩陣A的所有gj2都計算出來，按大小排列，就可以提煉最有影響力的公共因子。

<3>因子旋轉

這方面涉及較為簡單，我就簡單提一下

目的：建立因子分析模型不是隻要找主因子，更加重要的是意義，以便對實際進行分析，因子旋轉就是使所得結論更加清晰的表示。

方法：正交旋轉，斜交旋轉兩大類，常用正交。

便於理解，我解釋下旋轉的意義，以平面直角座標系為例，我們想得到的資料正好為：y=x和y=-x上的點，我們能解釋的卻在x=0和y=0上，這時候我們就可以旋轉座標系，卻不影響結果。這只是便於理解，沒有任何科學依據，覺得不對的請無視。

如果有任何演算法、程式碼疑問都歡迎通過公眾號發訊息給我哦，已經給你們準備好資料大禮包了。