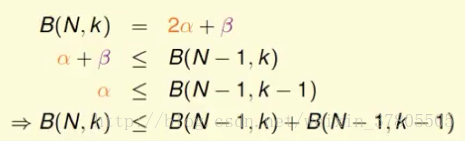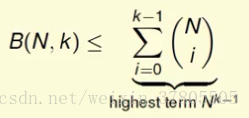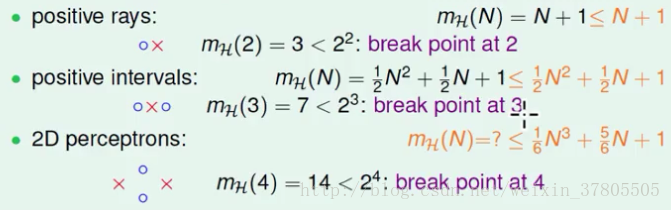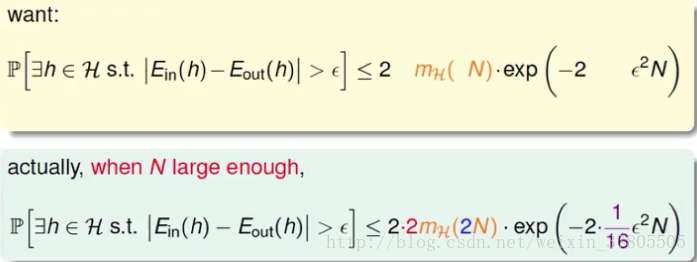機器學習基石第六講筆記
Lecture 6:theory of generalization一般化理論
6-1 Restriction of Break Points
成長函式m:假說h在n個點上可以產生多少個二分(dichotomies)。
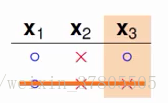
若正向o,反向×,則
理解程度一般,positive intervals為什麼xox可以呢?
這種情況認為x2和x3是被shatter的(4種情況都涵蓋全了)。
break point=2的意思:任意兩個點都不能shatter。
而這種情況是不能被shatter的,證明4種dichotomies是可以的。
而當5種dichotomies時,必有兩個x,所以肯定有兩個引數x是會被shatter的。
所以在這裡的maximum possible(也就是成長函式m)是4種。
上面的x1,x2,x3的情況是N=3的。
這節的fun time是break point=1,N=3時,只能有1種成長函式m,原因如圖:
第二種情況加進來,不管怎麼加,都會有一個引數x同時有x和o的情況。(此時假設的條件是一個都不能shatter)
6-2 Bounding Function (上限函式B)
關注的問題:到底可以做出多少種排列組合?
B(N,k)總共N個維度,任意k維都確保不能shatter,這時能有幾種dichotomies。
成長函式m和B的關係:m<B(B是m的上限)
當N<k時,就相當於任意N維不能shatter,所以此時是2^N。
當N=k時,全部結果是不能shatter的,所以要減一種,最後結果是2^N-1。
加上6-1最後兩圖的情況,目前有:
6-3 Bounding Function (上限函式B)-Inductive cases
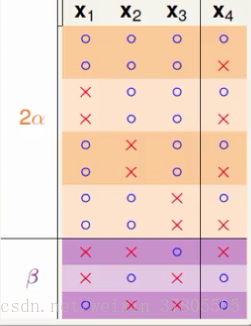
現在想做的是填寫6-2圖表中的其他值。
用程式找到B(4,3)=11 4+7=11=2alpha+beta
這時要求alpha+beta<B(3,3)且alpha<B(3,2) 故2alpha+beta<B(3,3)+B(3,2)
推廣到B(N,k) 有:
填寫完大致的表:
成長函式m的上限是上限函式B,上限函式B的上限是某個多項式函式poly(N)。
所以,我們可以得到結論:成長函式最多,也就只能夠和某個多項式函式的值一樣大。如圖:
6-4 A Pictorial Proof
本節的內容是講解公式中的三個常數是怎麼算出來的(不是從數學上,而是從邏輯上)。
這裡不做過多的講解啦(覺得不是重要的內容)。下次學第七課!
注:圖片全部來自臺大林軒田教授《機器學習基石》視訊課程截圖。