1、Wilcoxon Signed Rank Test

Wilcoxon有符號秩檢驗(也稱為Wilcoxon有符號秩和檢驗)是一種非引數檢驗。當統計資料中使用“非引數”一詞時，並不意味著您對總體一無所知。這通常意味著總體資料沒有正態分佈。如果兩個資料樣本來自重複觀察，那麼它們是匹配的。利用Wilcoxon Signed-Rank檢驗，在不假設資料服從正態分佈的前提下，判斷出相應的資料總體分佈是否相同如果資料對之間的差異是非正態分佈的，則應使用Wilcoxon有符號秩檢驗。

The Wilcoxon signed rank test (also called the Wilcoxon signed rank sum test) is
 
 a non-parametric test. When the word “non-parametric” is used in stats, it doesn’t quite mean that you know nothing about the population. It usually means that you know the population data does not have a normal distribution. The Wilcoxon signed rank test should be used if the differences between pairs of data are non-normally distributed.
 

有兩個稍微不同的測試版本:
Wilcoxon符號秩檢驗將樣本中值與假設中值進行比較。
Wilcoxon匹配對有符號秩檢驗計算每組匹配對之間的差異，然後按照與有符號秩檢驗相同的步驟將樣本與某個中值進行比較。

Two slightly different versions of the test exist:
    The Wilcoxon signed rank test compares your sample median against a hypothetical median.
    The Wilcoxon matched-pairs signed rank test computes the difference between each set of matched pairs, then follows the same procedure as the signed rank test to compare the sample against some median.
 

這個檢驗的零假設是兩個樣本的中位數相等。它通常用於:
作為單樣本t檢驗或配對t檢驗的非引數替代。
對於沒有數字刻度的有序(排序)分類變數。

The null hypothesis for this test is that the medians of two samples are equal. It is generally used:
    As a non-parametric alternative to the one-sample t test or paired t test.
    For ordered (ranked) categorical variables without a numerical scale.

2、How to Run the Test by Hand

執行測試的要求:
必須匹配資料。
因變數必須是連續的(即您必須能夠區分小數點後第n位的值)。
你應該沒有並列的隊伍，以達到最高的準確性。如果等級是相等的，有一個變通方法(見下面步驟5之後)。

Requirements for running the test:
    Data must be matched.
    The dependent variable must be continuous (i.e. you must be able to distinguish between values at the nth decimal place).
    You should have no tied ranks for maximum accuracy. If ranks are tied, there is a workaround (see below, after Step 5).

3、手動計算

樣本問題:以下2組治療資料的中值是否存在差異?

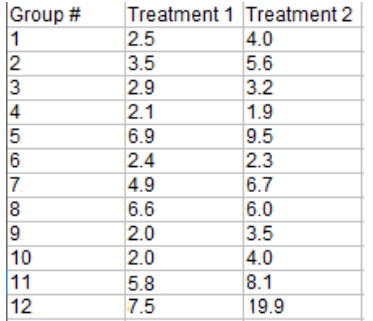
Step 1: 從治療1中減去治療2得到差異

注意:如果你只有一個樣本，計算每個變數和0之間的差(假設中值)，而不是對之間的差

Note: If you only have one sample, calculate the differences between each variable and zero (the hypothesized median) instead of the difference between pairs.

Step 2:將差異按順序排列(下圖第二列)，然後進行排序。按順序排列時忽略這個符號。

Step 3:建立第三列，並注意差異的符號(您在步驟2中忽略的那個)

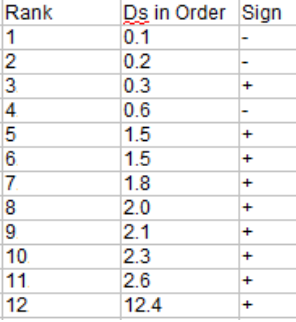
Step 4: 計算負差的秩和(第3步圖中帶負號的秩和)。你在這裡加起來，而不是實際的差異:

W^– = 1 + 2 + 4 = 7

Step 5:計算正差異的秩和(步驟3圖中帶正號的)。
W⁺ = 3 + 5.5 + 5.5 + 7 + 8 + 9 + 10 + 11 + 12 = 71

 Step 6:使用帶有Wilcoxin符號秩的正態逼近

 你可以利用以上資料做些什麼?如果觀測值/對 n(n+1)/2大於20，可以使用正態逼近。這組資料滿足這個要求(12(12 + 1)/ 2 = 78。z分數公式有幾個修改/注意事項:

使用W⁺或W^-中較小的值作為測試統計量。
使用以下公式的意思是,μ:n(n + 1)/ 4。
使用以下公式σ:√(n(n + 1)(2 n + 1)/ 24)
如果你有tied ranks,你必須減少t3-tσ/ 48 t的行列。有兩個並列排名(5.5 + 5.5),所以減少8-2/48σ= 0.125。

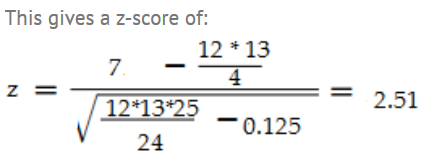
在z表中查詢這個分數，我們得到面積為0.9880，等於雙尾p值為0.012。這是一個很小的p值，這是一個強有力的跡象，表明中位數是顯著不同的。

4、用R計算Wilcoxin

在名為immer的內建資料集中，記錄了1931年和1932年同一領域的大麥產量。收益率資料顯示在資料框的Y1和Y2列中。

問題（problem）：在不假設資料為正態分佈的情況下，以0.05顯著性水平檢驗資料集immer中1931年和1932年的大麥產量是否具有相同的資料分佈。

5、Solution

零假設是兩個樣本年的大麥產量是相同的。為了驗證這個假設，我們使用wilcox。測試函式對匹配的樣本進行比較。對於配對測試，我們將“配對”引數設定為TRUE。由於p值為0.005318，小於0.05的顯著性水平，我們拒絕原假設。

The null hypothesis is that the barley yields of the two sample years are identical populations. To test the hypothesis, we apply the wilcox.test function to compare the matched samples. For the paired test, we set the "paired" argument as TRUE. As the p-value turns out to be 0.005318, and is less than the .05 significance level, we reject the null hypothesis. 

wilcox.test(immer$Y1, immer$Y2, paired=TRUE)