八大經典排序演算法
概述
排序有內部排序和外部排序,內部排序是資料記錄在記憶體中進行排序,而外部排序是因排序的資料很大,一次不能容納全部的排序記錄,在排序過程中需要訪問外存。我們這裡說說八大排序就是內部排序。
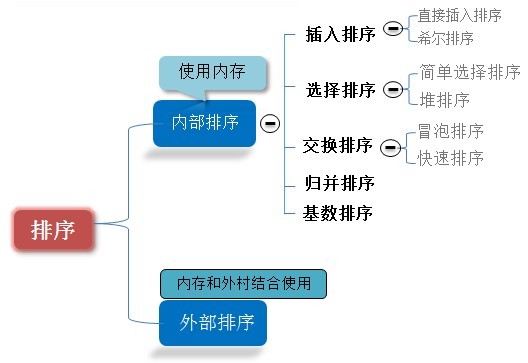
當n較大,則應採用時間複雜度為O(nlog2n)的排序方法:快速排序、堆排序或歸併排序序。
快速排序:是目前基於比較的內部排序中被認為是最好的方法,當待排序的關鍵字是隨機分佈時,快速排序的平均時間最短;
1.插入排序—直接插入排序(Straight Insertion Sort)
基本思想:
將一個記錄插入到已排序好的有序表中,從而得到一個新,記錄數增1的有序表。即:先將序列的第1個記錄看成是一個有序的子序列,然後從第2個記錄逐個進行插入,直至整個序列有序為止。
要點:設立哨兵,作為臨時儲存和判斷陣列邊界之用。
直接插入排序示例:
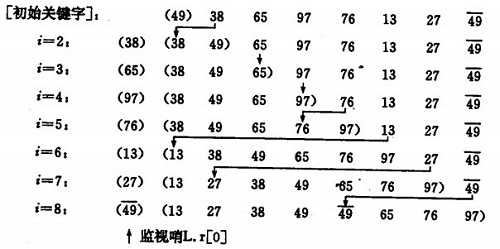
如果碰見一個和插入元素相等的,那麼插入元素把想插入的元素放在相等元素的後面。所以,相等元素的前後順序沒有改變,從原無序序列出去的順序就是排好序後的順序,所以插入排序是穩定的。
演算法的實現:
- void print(int a[], int n ,int i){
- cout<<i <<":";
- for(int j= 0; j<8; j++){
- cout<<a[j] <<" ";
- }
- cout<<endl;
- }
- void InsertSort(int a[], int n)
- {
- int x;int j;
for (int i = 1; i < n; i++) {
j = i - 1; // 要插入元素的下標
x = arr[i]; // 哨兵
for( ; j>=0 && x<a[j]; j--){
a[j+1] = a[j];
}
a[j + 1] = x; // 插入到正確的位置 - }
- print(a,n,i); //列印每趟排序的結果
- }
- int main(){
- int a[8] = {3,1,5,7,2,4,9,6};
- InsertSort(a,8);
- print(a,8,8);
- }
效率:
時間複雜度:O(n^2).
其他的插入排序有二分插入排序,2-路插入排序。
2. 插入排序—希爾排序(Shell`s Sort)
希爾排序是1959 年由D.L.Shell 提出來的,相對直接排序有較大的改進。希爾排序又叫縮小增量排序
基本思想:
先將整個待排序的記錄序列分割成為若干子序列分別進行直接插入排序,待整個序列中的記錄“基本有序”時,再對全體記錄進行依次直接插入排序。
操作方法:
- 選擇一個增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列個數k,對序列進行k 趟排序;
- 每趟排序,根據對應的增量ti,將待排序列分割成若干長度為m 的子序列,分別對各子表進行直接插入排序。僅增量因子為1 時,整個序列作為一個表來處理,表長度即為整個序列的長度。
希爾排序的示例:
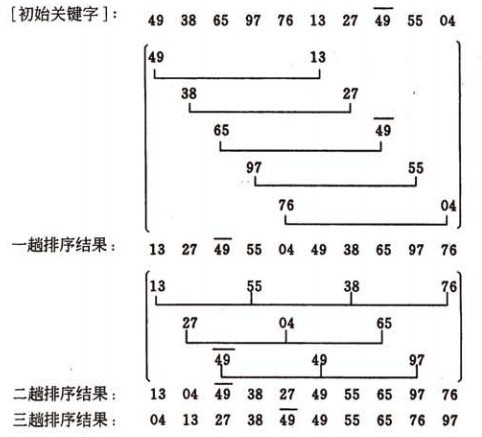
演算法實現:
我們簡單處理增量序列:增量序列d = {n/2 ,n/4, n/8 .....1} n為要排序數的個數
即:先將要排序的一組記錄按某個增量d(n/2,n為要排序數的個數)分成若干組子序列,每組中記錄的下標相差d.對每組中全部元素進行直接插入排序,然後再用一個較小的增量(d/2)對它進行分組,在每組中再進行直接插入排序。繼續不斷縮小增量直至為1,最後使用直接插入排序完成排序。
[cpp] view plain copy print?- void print(int a[], int n ,int i){
- cout<<i <<":";
- for(int j= 0; j<8; j++){
- cout<<a[j] <<" ";
- }
- cout<<endl;
- }
- /**
- * 直接插入排序的一般形式
- *
- * @param int dk 縮小增量,如果是直接插入排序,dk=1
- *
- */
- void ShellInsertSort(int a[], int n, int dk)
- {
- for(int i= dk; i<n; ++i){
- if(a[i] < a[i-dk]){ //若第i個元素大於i-1元素,直接插入。小於的話,移動有序表後插入
- int j = i-dk;
- int x = a[i]; //複製為哨兵,即儲存待排序元素
- a[i] = a[i-dk]; //首先後移一個元素
- while(j >= 0 && x < a[j]){ //查詢在有序表的插入位置
- a[j+dk] = a[j];
- j -= dk; //元素後移
- }
- a[j+dk] = x; //插入到正確位置
- }
- print(a, n,i );
- }
- }
- /**
- * 先按增量d(n/2,n為要排序數的個數進行希爾排序
- *
- */
- void shellSort(int a[], int n){
- int dk = n/2;
- while( dk >= 1 ){
- ShellInsertSort(a, n, dk);
- dk = dk/2;
- }
- }
- int main(){
- int a[8] = {3,1,5,7,2,4,9,6};
- //ShellInsertSort(a,8,1); //直接插入排序
- shellSort(a,8); //希爾插入排序
- print(a,8,8);
- }
希爾排序時效分析很難,關鍵碼的比較次數與記錄移動次數依賴於增量因子序列d的選取,特定情況下可以準確估算出關鍵碼的比較次數和記錄的移動次數。目前還沒有人給出選取最好的增量因子序列的方法。增量因子序列可以有各種取法,有取奇數的,也有取質數的,但需要注意:增量因子中除1 外沒有公因子,且最後一個增量因子必須為1。希爾排序方法是一個不穩定的排序方法。
3. 選擇排序—簡單選擇排序(Simple Selection Sort)
基本思想:
在要排序的一組數中,選出最小(或者最大)的一個數與第1個位置的數交換;然後在剩下的數當中再找最小(或者最大)的與第2個位置的數交換,依次類推,直到第n-1個元素(倒數第二個數)和第n個元素(最後一個數)比較為止。
簡單選擇排序的示例:
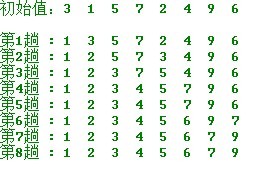
操作方法:
第一趟,從n 個記錄中找出關鍵碼最小的記錄與第一個記錄交換;
第二趟,從第二個記錄開始的n-1 個記錄中再選出關鍵碼最小的記錄與第二個記錄交換;
以此類推.....
第i 趟,則從第i 個記錄開始的n-i+1 個記錄中選出關鍵碼最小的記錄與第i 個記錄交換,
直到整個序列按關鍵碼有序。
演算法實現:
[cpp] view plain copy print?- void print(int a[], int n ,int i){
- cout<<"第"<<i+1 <<"趟 : ";
- for(int j= 0; j<8; j++){
- cout<<a[j] <<" ";
- }
- cout<<endl;
- }
- /**
- * 陣列的最小值
- *
- * @return int 陣列的鍵值
- */
- int SelectMinKey(int a[], int n, int i)
- {
- int k = i;
- for(int j=i+1 ;j< n; ++j) {
- if(a[k] > a[j]) k = j;
- }
- return k;
- }
- /**
- * 選擇排序
- *
- */
- void selectSort(int a[], int n){
- int key, tmp;
- for(int i = 0; i< n; ++i) {
- key = SelectMinKey(a, n,i); //選擇最小的元素
- if(key != i){
- tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素與第i位置元素互換
- }
- print(a, n , i);
- }
- }
- int main(){
- int a[8] = {3,1,5,7,2,4,9,6};
- cout<<"初始值:";
- for(int j= 0; j<8; j++){
- cout<<a[j] <<" ";
- }
- cout<<endl<<endl;
- selectSort(a, 8);
- print(a,8,8);
- }
簡單選擇排序的改進——二元選擇排序
簡單選擇排序,每趟迴圈只能確定一個元素排序後的定位。我們可以考慮改進為每趟迴圈確定兩個元素(當前趟最大和最小記錄)的位置,從而減少排序所需的迴圈次數。改進後對n個數據進行排序,最多隻需進行[n/2]趟迴圈即可。具體實現如下:
public void selectTwoSort(int a[], int n) {
int i;
for (i = 0; i <= n / 2; i++) { // i從0開始,不然第一個資料,就沒有參與比較
int min = i;
int max = n - i - 1;//最大資料指標應該這麼設定吧!
int tmp = 0;
int j;
for (j = i + 1; j < n - i - 1; j++) {
if (a[j] < a[min]) {
min = j;
continue;
}
if (a[j] > a[max]) {
max = j;
}
}
//放置最小值
tmp = a[min];
a[min] = a[i];
a[i] = tmp;
//放置最大值
tmp = a[max];
a[max] = a[n - i - 1];
a[n - i - 1] = tmp;
}
}