注：本系列來自於影象處理課程實驗，用Matlab實現最基本的影象處理演算法

影象點處理是影象處理系列的基礎，主要用於讓我們熟悉Matlab影象處理的程式設計環境。灰度線性變換和灰度拉伸是對畫素灰度值的變換操作，直方圖是對畫素灰度值的統計，直方圖均衡是對灰度值分佈的變換。

1.灰度線性變換

（1）線性變換函式

原圖向灰度值為g，通過線性函式f(x)=kx+b轉換為f(g)得到灰度的線性變換。

（2）程式碼實現

Matlab中支援矩陣作為函式引數傳入，定義一個線性轉換函式，利用Matlab矩陣操作，用一行程式碼即可對整個二維影象矩陣中所有點的灰度進行線性變換：

function
 
 [ new ] = LinearTransformFunc( original, k, d )
    new = original * k + d;
end

其中k和d是線性函式的斜率和截距，由使用者輸入指定，使用者輸入為空時賦予預設值：

• input函式獲取使用者輸入
• isempty判斷使用者輸入是否為空：

k = input('please input the slope(k) of grayscale linear transformation function:\n');

b = input('please input the intercept(b) of grayscale linear transformation function
 
:\n');

if isempty(k)
    k = 1;
end

if isempty(b)
    b = 0;
end

變換影象名也可以由使用者input指定，預設為lena圖:

• imread讀出圖片，返回值第一個是我們需要的灰度圖（二維矩陣）
• 對變換後的灰度圖，用imshow在figure中顯示影象

name = input('please input the name of image:\n');

if isempty(name) 
    name = 'lena'; 
end

original = imread(strcat('../exp/', name, '.bmp'));

transformed = LinearTransformFunc(original, k, b);

figure
imshow(transformed)
 

在這個實驗的操作中說明如何讀入、顯示，後面實驗不在贅述

（3）執行結果

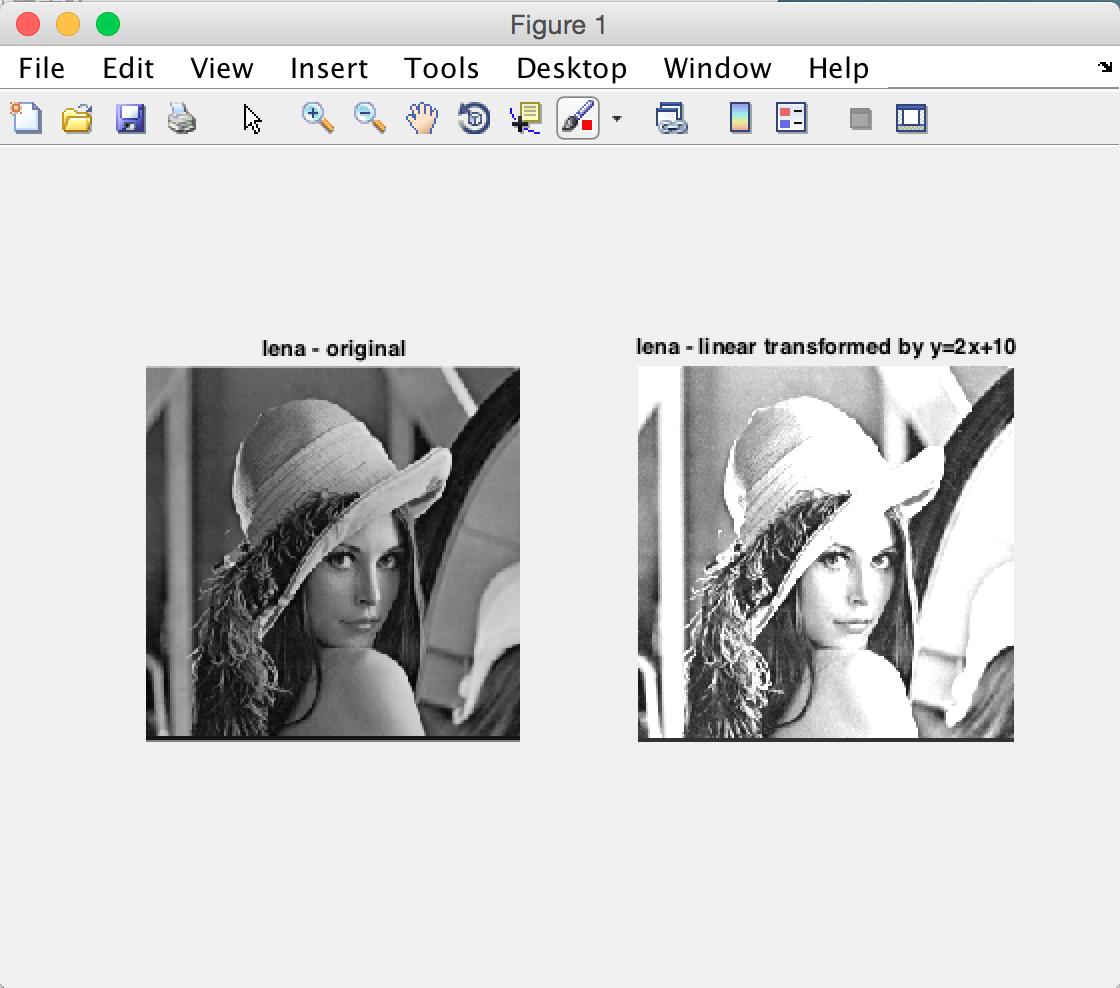
利用subplot作圖，把原圖和線性變換後的影象對比，線性變換函式是f(x)=2x+10:

左圖是原影象，右圖是線性變換後圖像。

2.灰度拉伸變換

（1）灰度拉伸變換和線性分段函式

灰度拉伸變換和線性變換相似，只是是將灰度值做分段線性變換。分段函式控制點(x1,y1)和(x2,y2)：

（2）程式碼實現

整個程式使用者介面和流程和線性變換相同，只是需要使用者輸入兩個控制點，並傳入以下的分段線性變換函式：

function [ new ] = StretchFunc(original, x1, y1, x2, y2 )
    new = original;

    w = size(new, 1);
    h = size(new, 2);

    k1 = y1 / x1;

    dk1 = (y2 - y1) / (x2 - x1);
    dk2 = (255 - y2) / (255 - x2);

    for i = 1 : w
        for j = 1 : h
            x = new(i, j);
            if x < x1
                new(i, j) = k1 * x;
            elseif x < x2
                new(i, j) = dk1 * (x - x1) + y1;
            else
                new(i, j) = dk2 * (x - x2) + y2;
            end
        end
    end
end

這裡不可避免要使用到for迴圈。

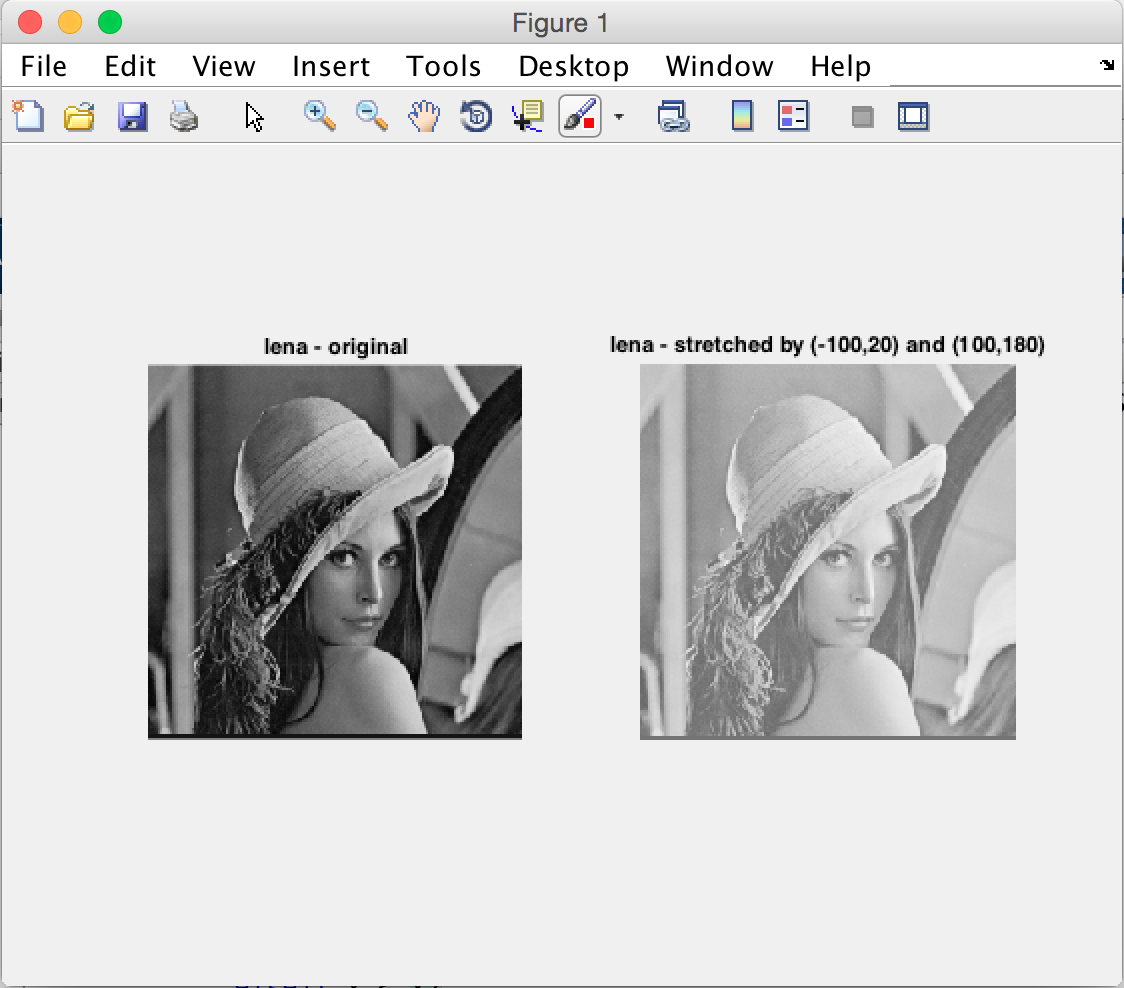
（3）執行結果

同樣對比原圖，預設控制點選取(-100,20)和(100,180)

3.灰度直方圖

（1）灰度直方圖

灰度直方圖就是對影象中每個畫素點的灰度值出現的頻數或頻率（歸一化）的統計，那麼我們直接遍歷整個影象統計出每個灰度值出現次數再做相應處理即可。

（2）程式碼實現

首先需要遍歷統計灰度，我在GrayScaleStatistic函式裡完成統計，區間[low, high]是目標灰度統計區間，預設是[0,255]：

function [ result ] = GrayScaleStatistic( original, low, high )

    w = size(original, 1);
    h = size(original, 2);
    result = zeros(1, high - low + 1);

    for i = 1 : w
        for j = 1 : h
            g = original(i, j);
            if g >= low && g <= high
                g = g - low + 1;
                result(g) = result(g) + 1; 
            end
        end
    end

end

然後就使用Matlab條形圖作圖函式bar完成灰度圖作圖：

y = GrayScaleStatistic(original, low, high);
x = low : 1 : high;
bar(x, y)

對於題目要求的可輸入灰度區間顯示，我們要麼不統計區間[low, high]以外的灰度值，要麼直接全部統計但在作圖時用xlim函式限制x軸取值範圍：

xlim([low, high])

（3）執行結果

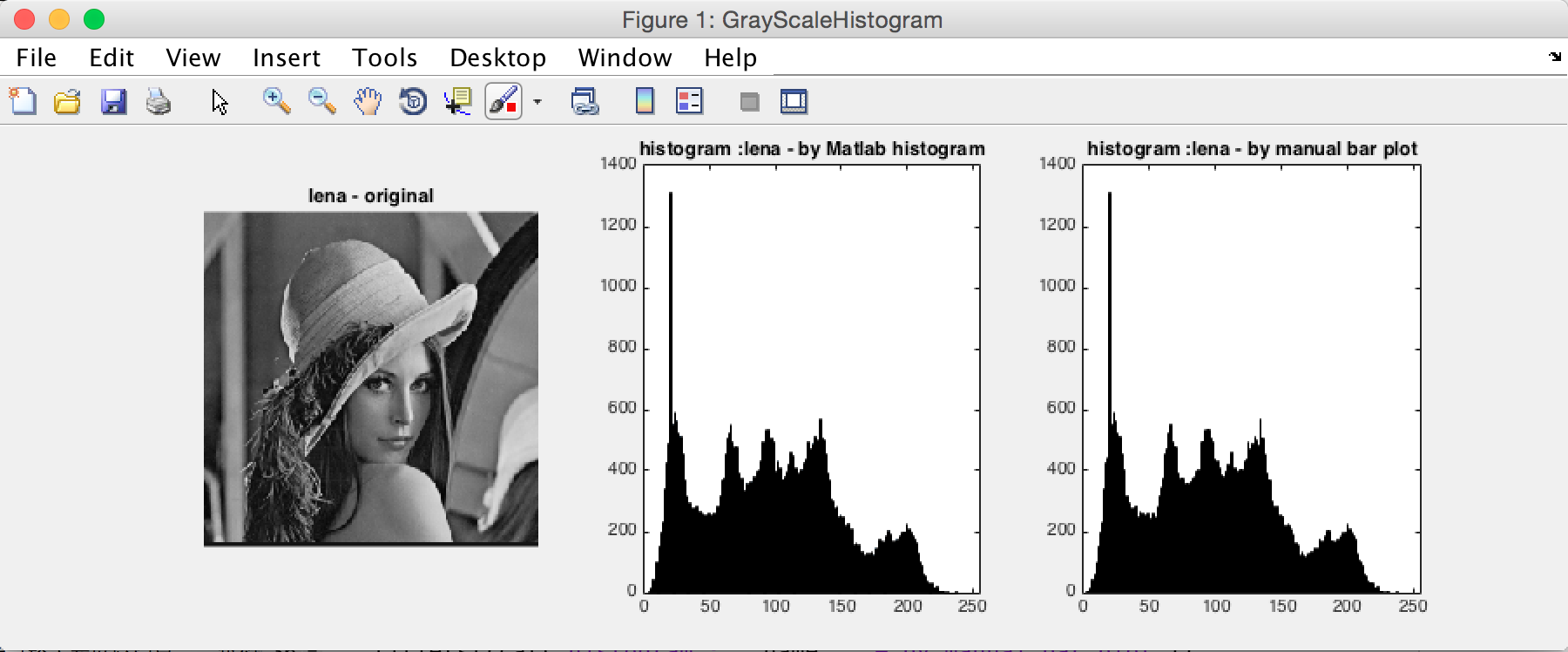
對比Matlab標準直方圖作圖函式histogram，結果如下：

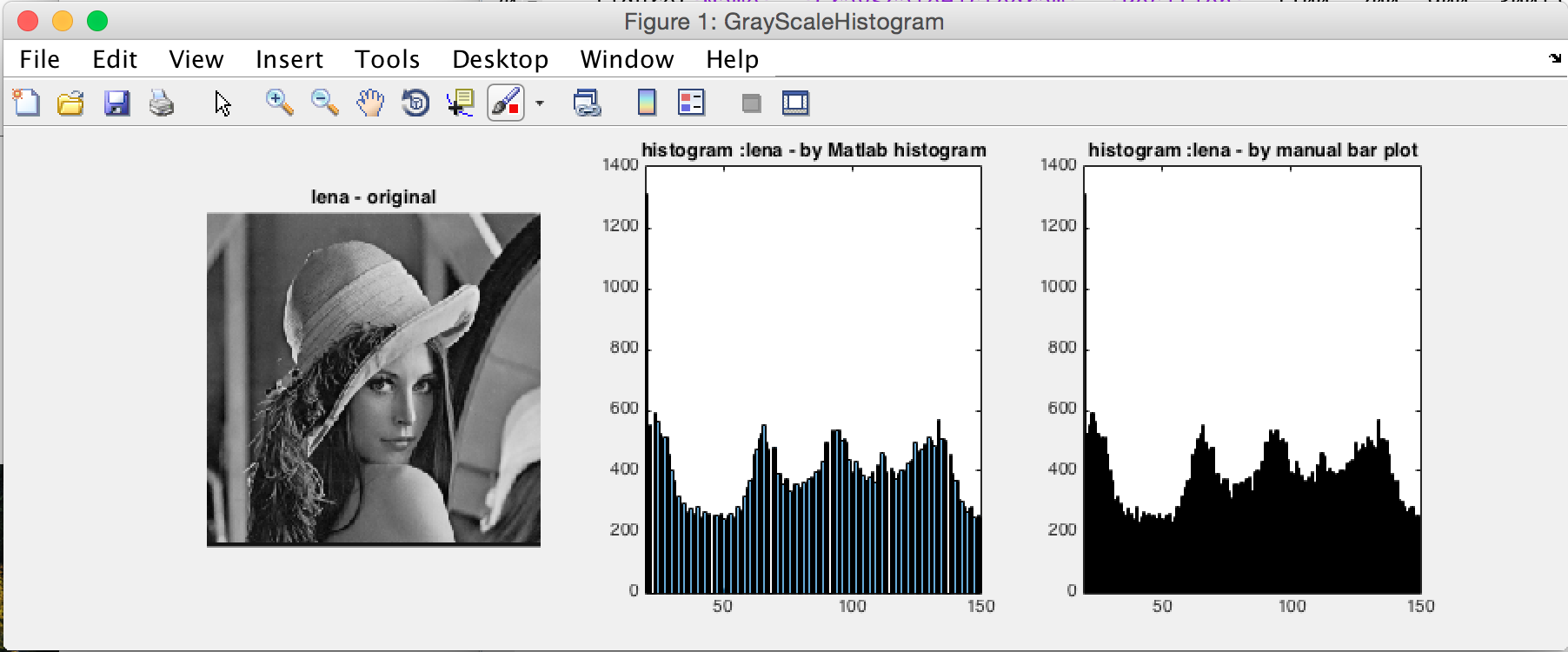
也可以通過input輸入限定區間，這裡是[20,150]區間的灰度直方圖：

左右對比，效果一致。

4.直方圖均衡化

（1）直方圖均衡演算法

直方圖均衡主要用於增強動態範圍偏小的影象的反差，其基本思想是把原始影象的直方圖變換為均勻分佈，從而增強灰度值的動態範圍，以達到增強對比度的效果。

直方圖均衡化演算法如下

1. 歸一化灰度頻數直方圖，得到頻率直方圖sk
2. 用sk計算頻率累計直方圖tk，
3. tk做取整擴充套件：tk = int[(L - 1) * tk + 0.5]，將直方圖灰度對映儘量滿整個灰度取值空間L
4. 確定變換對映關係k->tk
5. 根據對映關係變換影象灰度值

（2）程式碼實現

在指令碼中呼叫Normalize函式直接得到均衡化後的影象，再統計直方圖並顯示。

Normalize函式如下：

function [ new ] = Normalize( original, v )

    s = sum(v);
    tv = v / s;

    l = length(v);

    for i = 2 : l
        tv(i) = tv(i) + tv(i - 1);
    end

    tk = uint8(255 * tv + 0.5);

    w = size(original, 1);
    h = size(original, 2);

    new = original;

    for i = 1 : w
        for j = 1 : h
            new(i, j) = tk(original(i, j) + 1);
        end
    end

end

說明：

• tv先計算頻率直方圖，再通過累加得到累計直方圖
• tk根據累計直方圖計算新的灰度對映關係
• 最後遍歷整個影象把原灰度轉換成均衡化後的灰度值

其中有一下幾點需要注意，也是Matlab圖操作的注意點：

• Matlab預設型別是double，對灰度值賦值時注意強制轉換型別，保證型別一致
• Matlab座標起始從1開始，而灰度值是uint8的0-255，因此對映陣列tk把原始灰度對映到變換後灰度時需要加1

（3）結果展示

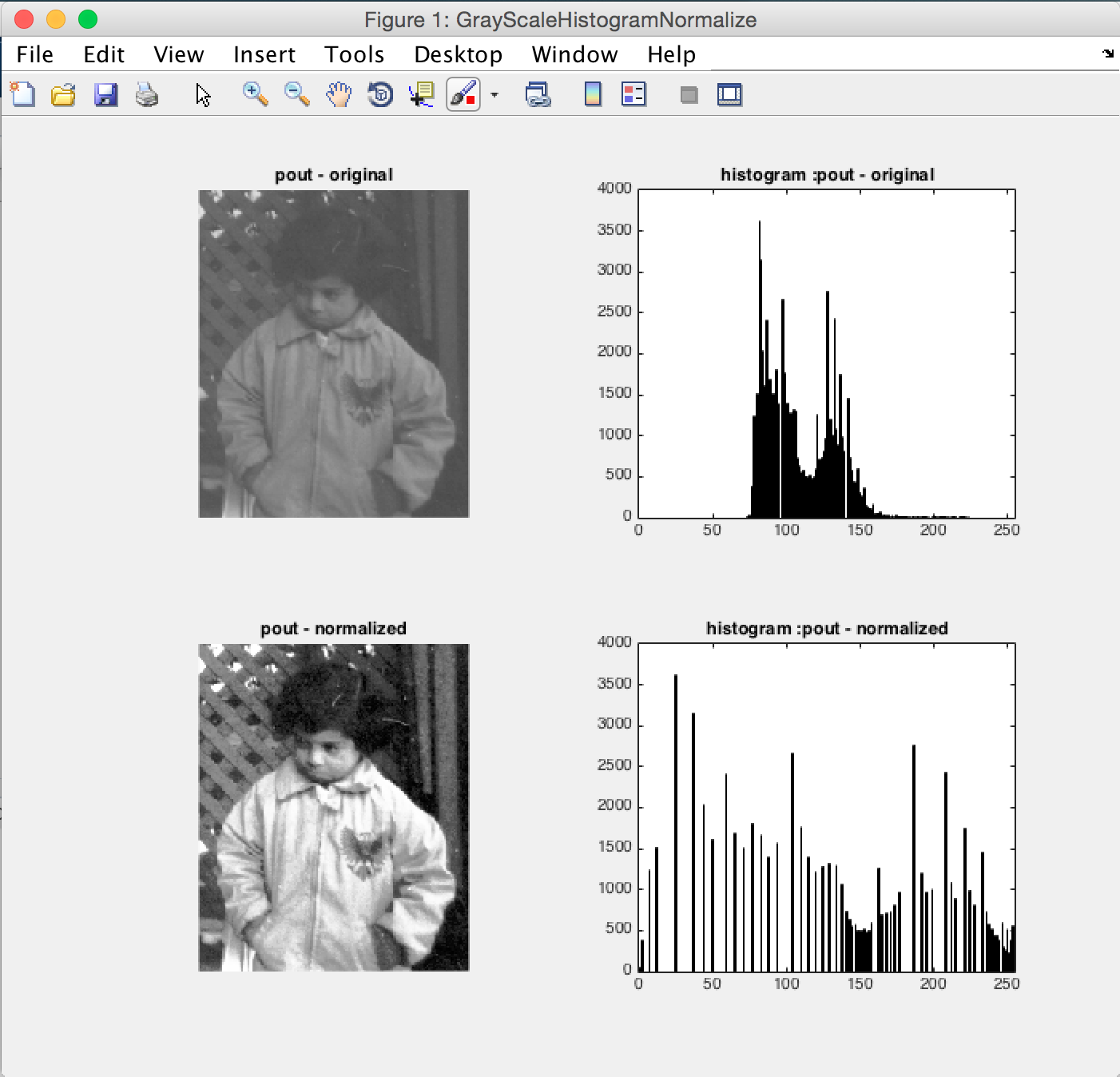
pout.bmp是一副灰度分佈較為集中的影象，因此影象對比度不高，顯示較為模糊。使用直方圖均值化，分散灰度分佈從而增強對比度：

通過對比均衡先後直方圖分佈，可以發現：

• 灰度分佈不能完全平均化，是由於均值化演算法中運用了取整運算，而不是離散值的完全均衡化
• 得到的均衡化後直方圖走勢沒有發生變化，因此影象沒有失真