前言

Keras原始碼中附有一個examples的資料夾，裡面包含一些使用Keras進行編寫的常用的神經網路模型，如CNN、LSTM、ResNet等。這些例子基本上是Keras學習入門必看的，作為Keras的學習者，就在這裡記錄一下examples中的程式碼解析，一為自身記憶，二為幫助他人。

原始碼

這裡解析的原始碼是變分自動編碼器（variational autoencoder，VAE），其是標準自動編碼器的一個升級版本。與標準自動編碼器相比，VAE在編碼器階段添加了一個約束，使產生的code服從單位高斯分佈。關於VAE的介紹可參考這裡。

VAE的示意圖如下：

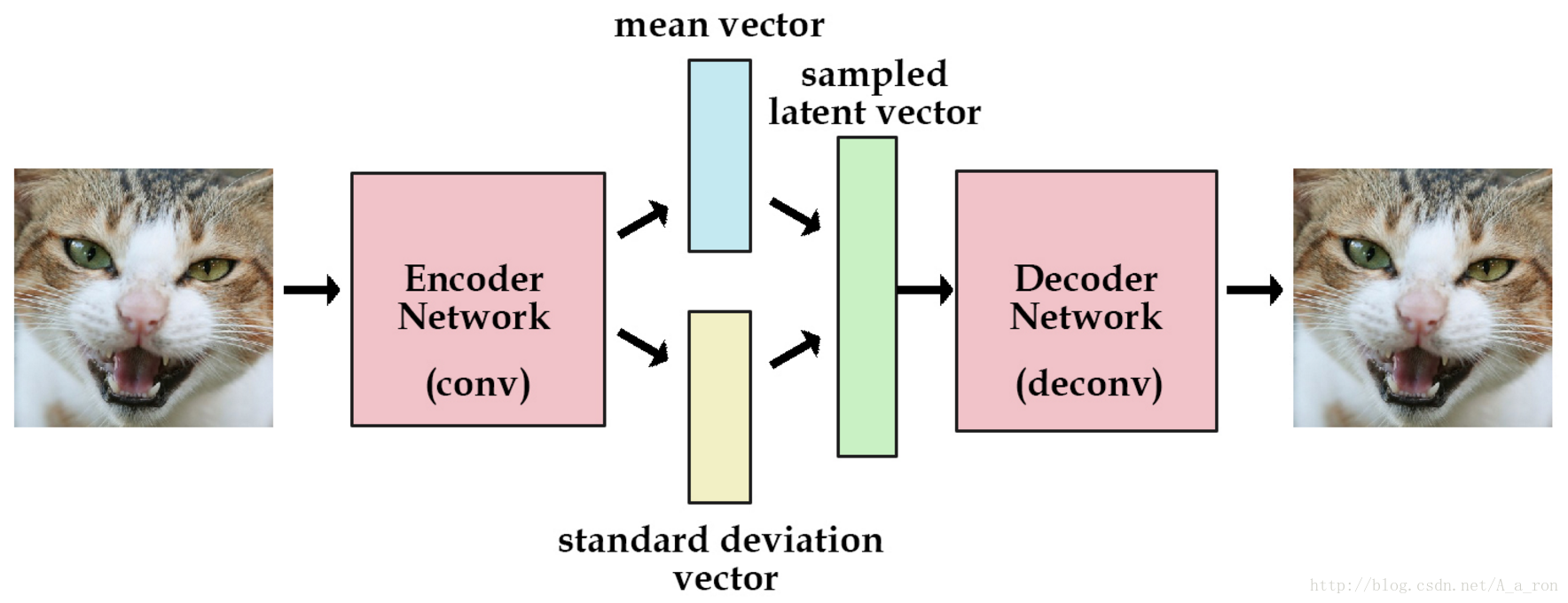
VAE的示例程式碼在Keras中的路徑為Keras/examples/variational_autoencoder.py

examples中的variational_autoencoder_deconv.py檔案中的程式碼是VAE的卷積網路實現的形式，兩者執行的結果很類似，程式碼上也很接近，大家可以參照這個來理解卷積網路版本的VAE。

#匯入相關包
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

from keras.layers import Input, Dense, Lambda, Layer
from
 
 keras.models import Model
from keras import backend as K
from keras import metrics
from keras.datasets import mnist

#整個網路的維度變化為：784->256->2->256->784
batch_size = 100
#原始輸入維度，28*28=784
original_dim = 784
#編碼後的code的維度
latent_dim = 2
#中間隱藏層的維度
intermediate_dim = 256
#迭代50次
epochs = 50
#初始化時的標準差
 

epsilon_std = 1.0

#編碼器的結構
x = Input(shape=(original_dim,))
h = Dense(intermediate_dim, activation='relu')(x)
# mean vector
z_mean = Dense(latent_dim)(h)
# standard deviation vector
z_log_var = Dense(latent_dim)(h)

#使用均值變數（mean vector）和標準差變數（standard deviation vector）合成隱變數
def sampling(args):
    z_mean, z_log_var = args
    #使用標準正態分佈初始化
    epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim), mean=0.,stddev=epsilon_std)
    #合成公式
    return z_mean + K.exp(z_log_var / 2) * epsilon

# note that "output_shape" isn't necessary with the TensorFlow backend
#z即為所要求得的隱含變數
z = Lambda(sampling, output_shape=(latent_dim,))([z_mean, z_log_var])

# we instantiate these layers separately so as to reuse them later
# 解碼器的結構
decoder_h = Dense(intermediate_dim, activation='relu')
decoder_mean = Dense(original_dim, activation='sigmoid')
h_decoded = decoder_h(z)
#x_decoded_mean 即為解碼器輸出的結果
x_decoded_mean = decoder_mean(h_decoded)

# Custom loss layer
#自定義損失層，損失包含兩個部分：圖片的重構誤差（均方差Square Loss）以及隱變數與單位高斯分割之間的差異（KL-散度KL-Divergence Loss）。
class CustomVariationalLayer(Layer):
    def __init__(self, **kwargs):
        self.is_placeholder = True
        super(CustomVariationalLayer, self).__init__(**kwargs)

    def vae_loss(self, x, x_decoded_mean):
        xent_loss = original_dim * metrics.binary_crossentropy(x, x_decoded_mean)#Square Loss
        kl_loss = - 0.5 * K.sum(1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)#KL-Divergence Loss
        return K.mean(xent_loss + kl_loss)

    def call(self, inputs):
        x = inputs[0]
        x_decoded_mean = inputs[1]
        loss = self.vae_loss(x, x_decoded_mean)
        self.add_loss(loss, inputs=inputs)
        # We won't actually use the output.
        return x

有關損失函式的推導，感興趣的可看這篇論文的推導

#將損失層加入網路
y = CustomVariationalLayer()([x, x_decoded_mean])
vae = Model(x, y)
vae.compile(optimizer='rmsprop', loss=None)

# train the VAE on MNIST digits
#使用MNIST資料集進行訓練
(x_train, y_train), (x_test, y_test) = mnist.load_data()
#影象資料歸一化
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
#將影象資料轉換為784維的向量
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))

#模型訓練設定
vae.fit(x_train,
        shuffle=True,
        epochs=epochs,
        batch_size=batch_size,
        validation_data=(x_test, None))

至此，整個網路的構建和訓練都結束，下面為測試的程式碼。

# build a model to project inputs on the latent space
#編碼器的網路結構，將輸入圖形對映為code，即隱含變數
encoder = Model(x, z_mean)

# display a 2D plot of the digit classes in the latent space
#將所有測試集中的圖片通過encoder轉換為隱含變數（二維變數），並將其在二維空間中進行繪圖
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
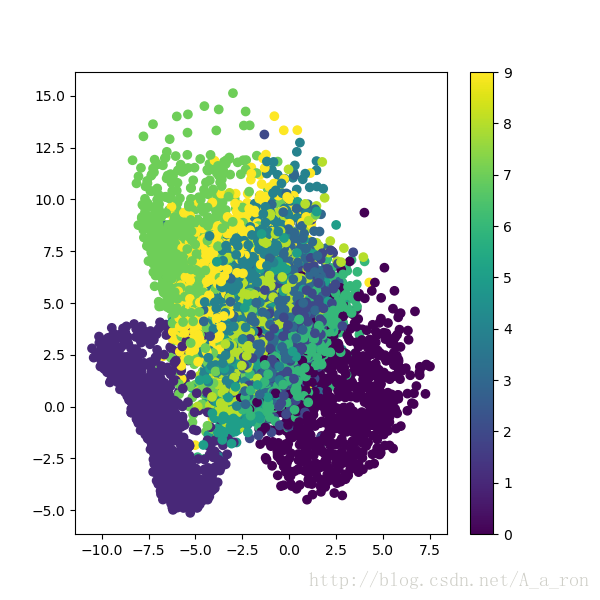
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()

測試集影象經過encoder之後在二維空間中的分佈如下：

# build a digit generator that can sample from the learned distribution
#構建一個解碼器，用於將隱變數解碼層圖片
decoder_input = Input(shape=(latent_dim,))
_h_decoded = decoder_h(decoder_input)
_x_decoded_mean = decoder_mean(_h_decoded)
generator = Model(decoder_input, _x_decoded_mean)

# display a 2D manifold of the digits
#繪製一個15個影象*15個影象的圖
n = 15  # figure with 15x15 digits
#每個影象的大小為28*28
digit_size = 28
#初始化為0
figure = np.zeros((digit_size * n, digit_size * n))
# linearly spaced coordinates on the unit square were transformed through the inverse CDF (ppf) of the Gaussian
# to produce values of the latent variables z, since the prior of the latent space is Gaussian
# 生成因變數空間（二維）中的資料，資料滿足高斯分佈。這些資料構成隱變數，用於影象的生成。
#ppf為累積分佈函式（cdf）的反函式，累積分佈函式是概率密度函式（pdf）的積分。np.linspace(0.05, 0.95, n)為累計分佈函式的輸出值（y值），現在我們需要其對應的x值，所以使用cdf的反函式，這些x值構成隱變數。
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))

有關scipy中的ppf函式可檢視這裡

#繪圖
for i, yi in enumerate(grid_x):
    for j, xi in enumerate(grid_y):
        z_sample = np.array([[xi, yi]])#add by weihao: 1*2
        x_decoded = generator.predict(z_sample)
        digit = x_decoded[0].reshape(digit_size, digit_size)#add by weihao: the generated image
        figure[i * digit_size: (i + 1) * digit_size,
               j * digit_size: (j + 1) * digit_size] = digit

plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r')
plt.show()

使用構建的隱含變數解碼出的影象如下圖所示：

可以看出，還是有一定的誤差的。