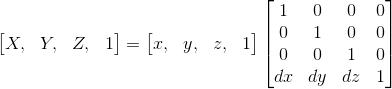三維座標系的旋轉矩陣
在進行影象程式開發的過程中,免不了要對影象做各種變換處理。有的時候變換可能比較複雜,比如平移之後又旋轉,旋轉之後又平移,又縮放。
直接用公式計算,不但複雜,而且效率低下。這時可以藉助變換矩陣和矩陣乘法,將多個變換合成一個。 最後只要用一個矩陣對每個點做一次處理就可以得到想要的結果。
另外,矩陣乘法一般有硬體支援,比如3D 圖形加速卡,處理3D變換中的大量矩陣運算,比普通CPU 要快上1000倍。
下面是3類基本的3D圖形變換: (2D圖形的變換相當於在3D的變換上減少一個維度即可)
一、平移:
設某點向x方向移動 dx, y方向移動 dy ,z方向移動dz, [x,y,z]為變換前座標, [X,Y,Z]為變換後坐標。
則 X = x+dx; Y = y+dy; Z =z+dz
以矩陣表示:
其中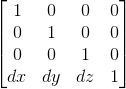
二、旋轉:
設某點與原點連線和X軸夾角為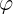
相關推薦
三維座標系的旋轉矩陣
在進行影象程式開發的過程中,免不了要對影象做各種變換處理。有的時候變換可能比較複雜,比如平移之後又旋轉,旋轉之後又平移,又縮放。 直接用公式計算,不但複雜,而且效率低下。這時可以藉助變換矩陣和矩陣乘法,將多個變換合成一個。 最後只要用一個矩陣對每個點做一次處理就可以得到想要的結果。 另外,矩陣乘法
圖形學1-三維座標系間的變換矩陣推導
概要:三維座標系的變換,實質上則是原點以及正交基向量的變化,在空間中表現為平移和旋轉。 如圖所示的座標系變換,可以用一個變換矩陣來表示。 雖然原理也比較簡單,但是大一學的線性代數已經有點忘記了。=////= 接下來,就當複習一下,我來推匯出這個變換矩陣是如何得到的,用到
三維座標旋轉轉換公式(JavaScript)
此方法以右手座標系為準 function rotate_z(x, y, z, angle) { var atopi = angle / 180 * Math.PI; var xtoz = x * Math.cos(ato
座標系旋轉矩陣推導過程
一、先來個平面旋轉的分析: 兩角和(差)公式 推導 旋轉變換一般是按照某個圓心點,以一定半徑 r 旋轉一定的角度α,為了簡單起見我們給出下面的情景 假定點A(x,y)想經過旋轉變換到達B(x',y'),已知旋轉角度α和點A
三維座標變換——旋轉矩陣與旋轉向量
https://blog.csdn.net/mightbxg/article/details/79363699 用 opencv 進行過雙目相機標定的同學都知道,單目標定 calibrateCamera() 函式能夠對每一張標定影象計算出一對 rvec 和 tvec,即旋轉平移向量,代表世界座標
座標系轉換之三:尤拉角、四元數、旋轉矩陣、方向餘弦矩陣、旋轉向量、軸角表示
座標轉換有很多種方法,不同的領域有不同的使用習慣。 上兩篇文章我們講了旋轉矩陣和尤拉角,可知尤拉角是可以由旋轉矩陣轉化而來。 那麼怎麼從尤拉角轉化為旋轉矩陣呢? 尤拉角(Euler angles)與旋轉矩陣(Rotation Matrix) 假設座標
任意三維直角座標系變換矩陣的推導
(v1, v2, v3)座標系 ==> (u1, u2, u3)座標系u1 =a1v1 + a2v2 + a3v3u2 =a4v1 + a5v2 + a6v3u3 =a7v1 + a8v2 + a9v3[ u ] = M [ v ]-------------------
Android OpenGL ES(六)----進入三維在程式碼中建立投影矩陣和旋轉矩陣
我們現在準備好在程式碼中新增透視投影了。Android的Matrix類為它準備了兩個方法------frustumM()和perspectiveM()。不幸的是,frustumM()的個缺陷,它會影響某些型別的投影,而perspectiveM()只是從Android的ICS
關於opengl中的三維矩陣平移,矩陣旋轉,推導過程理解 OpenGL計算機圖形學的一些必要矩陣運算知識 glTranslatef(x,y,z)glRotatef(angle,x,y,z)函式詳解
原文作者:aircraft 原文連結:https://www.cnblogs.com/DOMLX/p/12166896.html 為什麼引入齊次座標的變換矩陣可以表示平移呢? - Yu Mao的回答 - 知乎 https://www.zhihu.com/
三個歐拉角得到3x3旋轉矩陣
三維空間 ont pre sin cos rotation mic ati div 三維坐標系中,已知三個歐拉角alpha,beta,gamma,分別為繞x軸旋轉alpha角度,繞y軸旋轉beta角度,繞z軸旋轉gamma角度。則旋轉矩陣Rotation的求法如下: Ma
CSS3景深、三維變換屬性及旋轉三維立方體的實現
場景 htc 學歷 ati light range frame 焦距 說道 瀏覽器坐標系 在講正式語法之前,首先需要了解瀏覽器坐標系 這需要我們把瀏覽器界面想象成一個立體的場景 這是網上流傳很廣的瀏覽器坐標系圖片 從左到右的方向是瀏覽器x軸的正方向 從上到下的方向是瀏覽器
二維陣列(矩陣)順時針旋轉90°
1.先轉置 2.後調換列元素 public void rotate(int[][] matrix){ //矩陣轉置程式碼 &n
二維圖形的矩陣變換(三)——在WPF中的應用矩陣變換
over 底層 hit 過程 相對 duration != closed com 原文:二維圖形的矩陣變換(三)——在WPF中的應用矩陣變換UIElement和RenderTransform 首先,我們來看看什麽樣的對象可以進行變換。在WPF中,用於呈現給用戶的對象的基
三維場景中路徑動畫處理動畫物體如何旋轉的理論
1、考慮兩向量是否平行或者其中一個向量為零向量,那麼叉乘的結果如何? 解析:如果兩向量a、b平行或者任意一個為零向量,那麼a ^ b = 0;(^為叉乘符號)。叉乘對零向量的解釋為:零向量平行於任意其
matlab 矩陣繪三維圖
axis off;% 去掉座標軸 axistight;% 緊座標軸 axisequal;% 等比座標軸 axis([-0.1, 8.1, -1.1, 1.1]);% 座標軸的顯示範圍 % gca: gca, h=figure(...); set(gca,'XLi
python 二維矩陣轉三維矩陣
>>> import numpy as np >>> a = np.arange(12).reshape(3,4) >>> a array([[ 0, 1, 2, 3], [ 4, 5, 6,
三維空間座標系變換——旋轉矩陣
空間中三維座標變換一般由三種方式實現,第一種是旋轉矩陣和旋轉向量;第二種是尤拉角;第三種是四元數。這裡先介紹旋轉矩陣(旋轉向量)與尤拉角實現三維空間座標變換的方法以及兩者之間的關係。 這裡以常見的世界座標系與相機座標系間的變換為例。 一、首先介紹從相機座標系
Unity3d使用 NGUI 做球形三維旋轉 UI
因為工作的需要研究了一下NGUI做球形三維旋轉的UI,初步作出了一個雛形,現在拿出來和大家分享,如果我有哪裡寫錯了或者做的不好請指出並給我一些建議。 我在這裡用的是2.6版本的NGUI,3.0版本的OnFinished較2.6版本有一點點的改進,如下 void Start
圓柱上直線切口,形成三維靜態座標系方程
圓柱上直線切口,形成三維靜態座標系方程為: X=R*COS(θ); &n
openGL三維網格座標,旋轉,縮放,燈光設定,紋理讀取,模型讀取(MFC單文件)
1.三維網格座標建立 2.基本3維圖形建立 3.滑鼠相應旋轉縮放 4.鍵盤相應旋轉縮放 5.燈光設定 6.紋理載入對映 7.讀取模型 關於MFC配置編寫openGL網上有很多教程 需要的函式建立一般是: OnCreat()