座標系旋轉矩陣推導過程
一、先來個平面旋轉的分析:
兩角和(差)公式

推導
旋轉變換一般是按照某個圓心點,以一定半徑 r 旋轉一定的角度α,為了簡單起見我們給出下面的情景
假定點A(x,y)想經過旋轉變換到達B(x',y'),已知旋轉角度α和點A座標,計算出點B

要計算點B則分別計算他的x'和y'分量

根據矩陣乘法計算規則,可以推出

只要給出旋轉角度,計算出矩陣,然後使用這個矩陣分別左乘每一個點,就能計算出這個點旋轉後的點座標 這樣我們就可以通過矩陣變換座標了
二、延伸到三維座標:
座標的旋轉變換在很多地方都會用到,比如機器視覺中的攝像機標定、影象處理中的影象旋轉、遊戲程式設計等。
任何維的旋轉可以表述為向量與合適尺寸的方陣的乘積。最終一個旋轉等價於在另一個不同座標系下對點位置的重新表述。座標系旋轉角度θ則等同於將目標點圍繞座標原點反方向旋轉同樣的角度θ。
若以座標系的三個座標軸X、Y、Z分別作為旋轉軸,則點實際上只在垂直座標軸的平面上作二維旋轉。
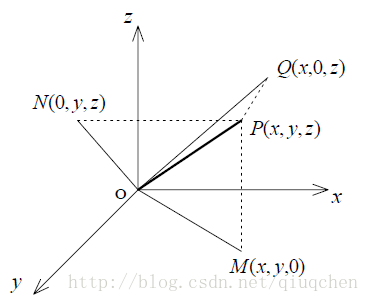
假設三維座標系中的某一向量,其在直角座標系中的圖如圖1所示。其中點P在XY平面、XZ平面、YZ平面的投影分別為點M、點P、點N。
圖1 直角座標系XYZ
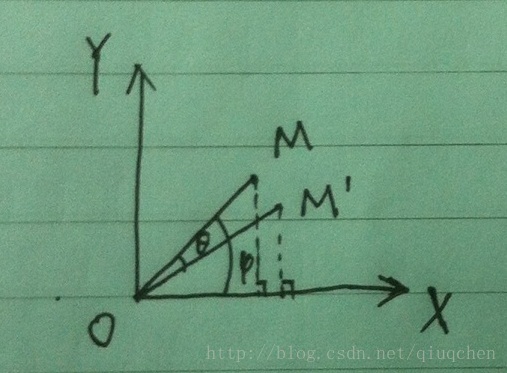
繞Z軸旋轉,相當於在XY平面的投影OM繞原點旋轉,如下圖所示,OM旋轉θ角到OM'。
圖2 向量繞Z軸旋轉示意圖
設旋轉前的座標為,旋轉後的座標為
,則點M的座標為
,點M'的座標為
。由此可得:



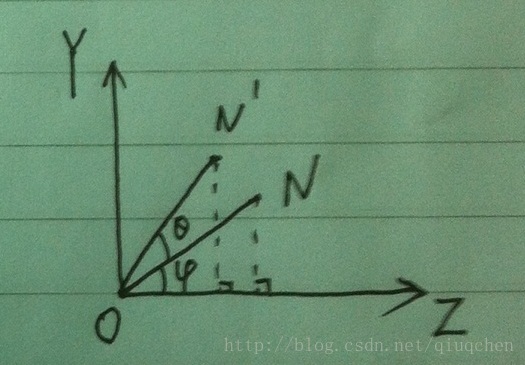
繞X軸旋轉,相當於在YZ平面的投影ON繞原點旋轉,如下圖所示,ON旋轉θ角到ON'。
圖3 向量繞X軸旋轉示意圖
設旋轉前的座標為,旋轉後的座標為
,則點N的座標為
,點N'的座標為
。由此可得:



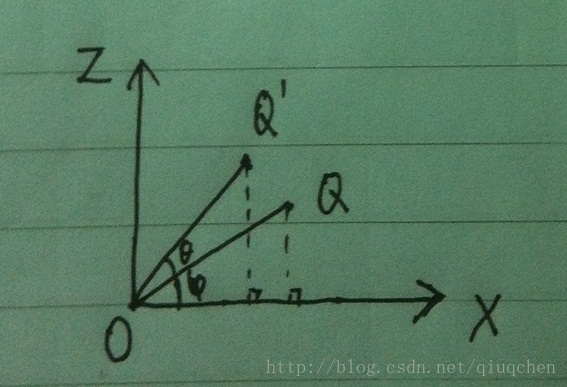
繞Y軸旋轉,相當於在XZ平面的投影OQ繞原點旋轉,如下圖所示,OQ旋轉θ角到OQ'。
圖4 向量繞Y軸旋轉示意圖
設旋轉前的座標為,旋轉後的座標為
,則點Q的座標為
,點Q'的座標為
。由此可得:



4、繞X、Y、Z軸旋轉的旋轉矩陣分別為: