Ordinary Least Square 最小二乘法

提到最小二乘法要先提到擬合，擬合Fitting是數值分析的基礎工具之一，在二維平面上分為直線擬合和曲線擬合，直線擬合找到一條直線儘可能穿過所有的點，注意這裡是儘可能，因為只要超過2個點，就有可能發生直線不能精確穿過所有點的情況，這時確定直線的原則有很多種，最小二乘法就是其中的一種，當直線不能穿過點時產生誤差（點和直線的距離），最小二乘法就是讓所有點的誤差的平方和最小；

最小二乘法（又稱最小平方法）是一種數學優化技術。它通過最小化誤差的平方和尋找資料的最佳函式匹配。利用最小二乘法可以簡便地求得未知的資料，並使得這些求得的資料與實際資料之間誤差的平方和為最小。

直線擬合（線性迴歸）過程如下圖：

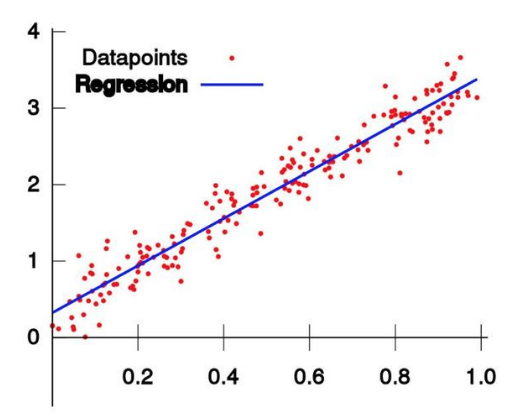
來看標準定義：

對給定資料點集合  ，在取定的函式類  中，求  ，使誤差的平方和  最小，  。從幾何意義上講，就是尋求與給定點集 的距離平方和為最小的曲線y=p(x)。函式p(x)稱為擬合函式或最小二乘解，求擬合函式p(x)的方法稱為曲線擬合的最小二乘法。

假設直線方程為

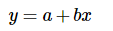
則誤差為

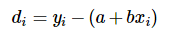
其中di表示(xi, yi)點的誤差

所有誤差的平方和為

這是一個2次函式，2次函式曲線如圖：

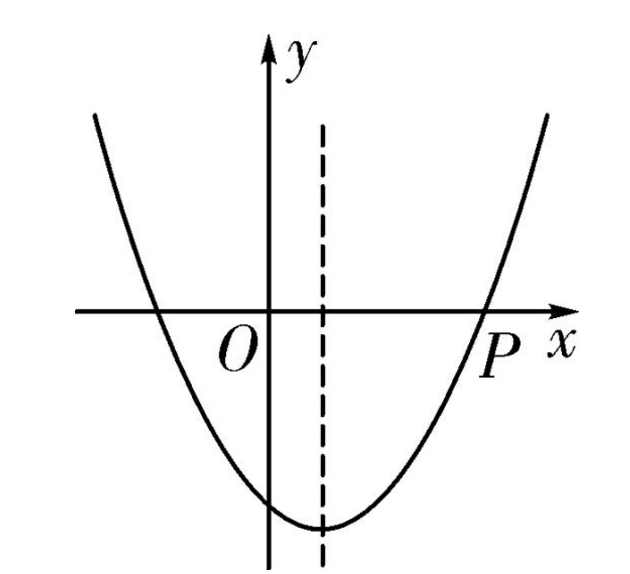
2次函式中D的最小值位於導數等於0的點，所以計算D對a和b的兩個偏導數為0即可得到兩個關於a和b的方程，

最終計算得出a和b的計算公式為：

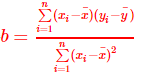
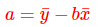
公式推導過程詳見 https://www.cnblogs.com/paiandlu/p/7843236.html