深度學習發展到如今的地位，離不開下面這 6 段程式碼。本文介紹了這些程式碼的創作者及其完成這些突破性成就的故事背景。每個故事都有簡單的程式碼示例，讀者們可以在 FloydHub 和 GitHub 找到相關程式碼。

最小二乘法

所有的深度學習演算法都始於下面這個數學公式（我已將其轉成 Python 程式碼）

1. # y = mx + b %一個一次線性方程
2. # m is slope, b is y-intercept %斜率和截距
3. def compute_error_for_line_given_points(b,m,coordinates):  
4.    totalError = 0
5.    for
    i in range(0,len(coordinates)):  
6.       x = coordinates[i][0]  
7.       y = coordinates[i][1]  
8.       totalError += (y-(m*x+b))**2
9.    return totalError/float(len(coordinates))  
10. # example
11. compute_error_for_line_given_points(1,2,[[3,6],[6,9],[12,18]])  

最小二乘法在 1805 年由 Adrien-Marie Legendre 首次提出（1805, Legendre），這位巴黎數學家也以測量儀器聞名。他極其痴迷於預測彗星的方位，堅持不懈地尋找一種可以基於彗星方位歷史資料計算其軌跡的演算法。

他嘗試了許多種演算法，一遍遍試錯，終於找到了一個演算法與結果相符。Legendre 的演算法是首先預測彗星未來的方位，然後計算誤差的平方，最終目的是通過修改預測值以減少誤差平方和。而這也正是線性迴歸的基本思想。

讀者可以在 Jupyter notebook 中執行上述程式碼來加深對這個演算法的理解。m 是係數，b 是預測的常數項，coordinates 是彗星的位置。目標是找到合適的 m 和 b 使其誤差儘可能小。

這是深度學習的核心思想：給定輸入值和期望的輸出值，然後尋找兩者之間的相關性。

1、概念簡介

根據維基百科的說明：

         最小二乘法（又稱最小平方法）是一種數學優化

         看了之後一頭霧水對不對，是的，任何人看著一段不知道在說啥。下面舉個例子，就很好懂了。

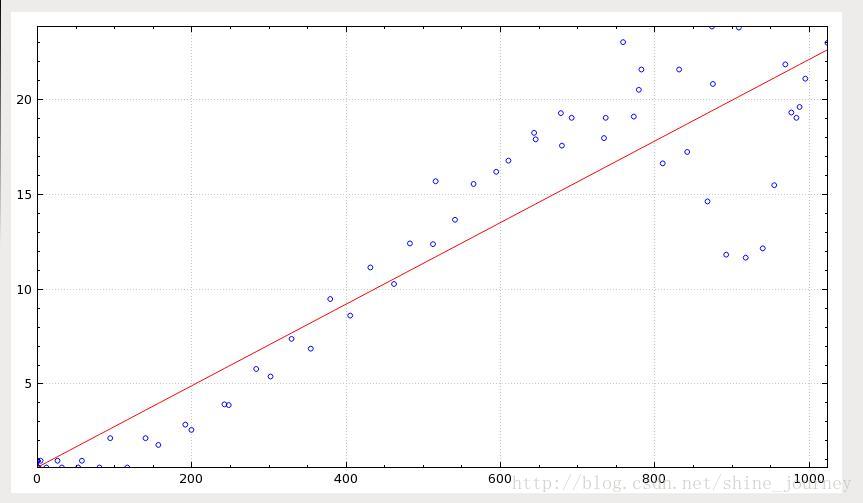
         針對線性最小二乘法即直線擬合，如下圖（來自維基百科）所示：

         透過這張圖，我想大家一定能理解，我們用最小二乘法來做什麼事情，即：

         根據已有的資料（圖中的藍色點），來做出一條最貼近資料發展趨勢的直線。通過這條直線，我們可以對未來的資料進行預測，因為基本會落在這條直線附近。

         當然了，最小二乘法不只是直線，還可以是曲線，本文不討論。

2、求解直線方程

（1）最小二乘法原理：

    在我們研究兩個變數（x,y）之間的相互關係時，通常可以得到一系列成對的資料（x1,y1）（x2,y2）（....）（xm,ym）；將這些資料描繪在x-y直角座標系中，若發現這些點在一條直線附近，可以令這條直線方程如（式1-1）。

　　yi = a*xi + b                        （式1-1)

　　其中：a、b 是任意實數

（2）常見擬合曲線：

       直線：    y=a*x+b

      多項式：最小二乘法資料擬合一般次數不易過高.

      雙曲線：  y=a/x+b

      指數曲線： y=a*e^b

      matlab中函式:P=polyfit(x,y,n)

     polyval（P，t）：返回n次多項式在t處的值

我們現在要做的，就是求解直線方程。

假設已知有N個點具有線性相關關係，（x1,y1）, （x2,y2）,…,（xn,yn）且實數xi不全相等，

設這條直線方程為：  y = m·x + c ，求斜率m和截距c，使得所有點相對於該直線的偏差平方和達到最小。

         解：設實數xi不全相等，所求直線方程為：y= a·x + b

                   要確定a，b，使得函式f(a,b) =∑ni=(yi - (a*xi+b))²最小，

其中，a和b的計算公式如下：

本文對於推導過程簡單講述，網上都有。

3、線性迴歸

　　線性迴歸假設資料集中特徵與結果存在著線性關係；

　　等式：y = mx + c

y為結果，x為特徵，m為係數，c為誤差在數學中m為梯度c為截距

　　這個等式為我們假設的，我們需要找到m、c使得mx+c得到的結果與真實的y誤差最小，這裡使用平方差來衡量估計值與真實值得誤差（如果只用差值就可能會存在負數）；用於計算真實值與預測值的誤差的函式稱為：平方損失函式（squard loss function）；這裡用L表示損失函式，所以有：

　　整個資料集上的平均損失為：

　　我們要求得最匹配的m與c使得L最小；數學表示式可以表示為：

　　最小二乘法用於求目標函式的最優值，它通過最小化誤差的平方和尋找匹配項所以又稱為：最小平方法；這裡將用最小二乘法用於求得線性迴歸的最優解；

最小二乘法

　　為了方便講清楚最小二乘法推導過程這裡使用，資料集有1…N個數據組成，每個資料由、構成，x表示特徵，y為結果；這裡將線性迴歸模型定義為：

平均損失函式定義有：

　　要求得L的最小，其關於c與m的偏導數定為0，所以求偏導數，得出後讓導數等於0，並對c與m求解便能得到最小的L此時的c與m便是最匹配該模型的；

關於c偏導數：

因為求得是關於c的偏導數，因此把L的等式中不包含c的項去掉得：

整理式子把不包含下標n的往累加和外移得到：

對c求偏導數得：

關於m的偏導數：

求關於m的偏導數，因此把L等式中不包含項去掉得：

　　整理式子把不包含下標n的往累加和外移得到：

對m求偏導數得：

令關於c的偏導數等於0，求解：

從上求解得到的值可以看出，上面式子中存在兩個平均值，因此該等式也可以改寫成：

令關於m的偏導數等於0，求解：　　關於m的偏導數依賴於c，又因為已經求得了關於c偏導數的解，因此把求關於c偏導數的解代數關於m的偏導數式子得：

合併含有m的項化簡：

求解：

為了簡化式子，再定義出：

C#演算法程式碼如下：

//-------------------------------------------------------------
//功能 : 最小二乘法直線擬合 y = a·x+ b，計算係數a和 b
//引數 : x –橫座標陣列
//       y --  縱座標陣列
//       num 是陣列包含的元素個數，x[]和y[]的元素個數必須相等
//       a,b 都是返回值
//返回 : 擬合計算成功返回true, 擬合計算失敗返回false
//-------------------------------------------------------------
bool leastSquareLinearFit(float x[], float y[], const int num, float &a,float &b)
{
    float sum_x2 = 0.0;
    float sum_y  = 0.0;
    float sum_x  = 0.0;
    float sum_xy = 0.0;

    try

      {
        for (int i = 0; i < num; ++i)

           {
            sum_x2 += x[i]*x[i];
            sum_y  += y[i];
            sum_x  += x[i];
            sum_xy += x[i]*y[i];
        }
    }

     catch (...)

      {
        return false;
    }
    a = (num*sum_xy - sum_x*sum_y)/(num*sum_x2 - sum_x*sum_x);
    b = (sum_x2*sum_y - sum_x*sum_xy)/(num*sum_x2-sum_x*sum_x);

    return true;
}

 資料樣本：

x：

float temp[96] = {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1.46667, 11.4667, 31.6, 52.7333, 80.3333, 116.333, 156.6, 199.4, 242.2, 283.4, 329.2, 379.333, 431.333, 482.6, 541, 594.4, 643.533, 692.133, 736.267, 772.667, 810.133, 841.867, 868.2, 892.4, 917.667, 939.8, 954.667, 969, 976.8, 983.4, 987.467, 994.933, 1023.67, 875.2, 873.933, 758.8, 678.2, 515.867, 782.533, 908.8, 779.2, 831.4, 645.533, 734.067, 679.533, 610.267, 565.067, 512.467, 462, 405.2, 354.133, 302, 247.8, 191.533, 140, 94.2667, 57.5333, 25.9333, 4, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }; // x

y：

float tempy[96] = {0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 0.595, 1.785, 2.57833, 3.927, 5.79233, 7.379, 9.48133, 11.1473, 12.4167, 13.6627, 16.193701, 18.248699, 19.042, 19.042, 19.105301, 16.6383, 17.240999, 14.631, 11.8217, 11.663, 12.155, 15.488, 21.859301, 19.32, 19.042, 19.6133, 21.105, 22.9937, 20.827299, 23.858299, 23.0333, 19.2883, 15.6937, 21.5893, 23.802999, 20.518299, 21.5893, 17.907301, 17.971001, 17.574301, 16.781, 15.5513, 12.3773, 10.2747, 8.60867, 6.86333, 5.39567, 3.88767, 2.856, 2.142, 2.142, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952, 0.952 }; // y    


計算結果：

a = 0.0215136

b = 0.608488


效果如下：