主成分分析（principal components analysis，PCA）是一個簡單的機器學習演算法，主要思想是對高維資料進行降維處理，去除資料中的冗餘資訊和噪聲。
演算法：
輸入樣本：D={x1,x2,⋯,xm}
低緯空間的維數

過程：·
1：對所有樣本進行中心化：xi←xi−1m∑mi=1xi；
2：計算所有樣本的協方差矩陣：XXT；
3:對協方差矩陣XXT做特徵值分解；
4：取最大的d′個特徵值做所對應的特徵向量w1,w2,⋯,wd′.
輸出：投影矩陣W=(w1,w2,⋯,wd′)
PCA演算法主要用在影象的壓縮，影象的融合，人臉識別上：

PCA

在python的sklearn包中給出了PCA的介面：

from sklearn.decomposition import PCA
import numpy as np

X=np.array([[-1,-1],[-2,-1],[-3,-2],[1,1],[2,1],[3,2]])
#pca=PCA(n_components=2)
pca=PCA(n_components='mle')
pca.fit(X)
print(pca.explained_variance_ratio_)

以自己造的資料集進行測試並測試
程式提取了一個特徵值

對二維資料進行降維

用PCA演算法對testSet.txt資料集進行降維處理

import numpy as np
import matplotlib.pyplot as plt


def loadDataSet(filename, delim='\t'):
    fr = open(filename)
    StringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [map(float, line) for line in StringArr]
    return np.mat(datArr)


def pca(dataMat, topNfeat=9999999
 
):
    meanVals = np.mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals  # remove mean
    covMat = np.cov(meanRemoved, rowvar=0)  # 尋找方差最大的方向a,Var(a'X)=a'Cov(X)a方向誤差最大
    eigVals, eigVects = np.linalg.eig(np.mat(covMat))
    eigValInd = np.argsort(eigVals)  # sort, sort goes smallest to largest
    eigValInd = eigValInd[:-(topNfeat + 1):-1]  # cut off unwanted dimensions
    redEigVects = eigVects[:, eigValInd]  # reorganize eig vects largest to smallest
    lowDDataMat = meanRemoved * redEigVects  # transform data into new dimensions
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat


dataMat = loadDataSet( 'testSet.txt')
print(dataMat)
lowDMat, recoMat = pca(dataMat, 1)
print(u'特徵值是：')
print(lowDMat)
print(u'特徵向量是：')
print(recoMat)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(np.array(dataMat[:, 0]),np.array(dataMat[:, 1]), marker='^', s=90)
ax.scatter(np.array(recoMat[:, 0]), np.array(recoMat[:, 1]), marker='o', s=50, c='red')
plt.show()


def replaceNanWithMean():
    datMat = loadDataSet('secom.data', ' ')
    numFeat = np.shape(datMat)[1]
    for i in range(numFeat):
        meanVal = np.mean(datMat[np.nonzero(~np.isnan(datMat[:, i].A))[0], i])
        datMat[np.nonzero(np.isnan(datMat[:, i].A))[0], i] = meanVal
    return datMat


dataMat = replaceNanWithMean()
meanVals = np.mean(dataMat, axis=0)
meanRemoved = dataMat - meanVals  # remove mean
covMat = np.cov(meanRemoved, rowvar=0)
eigVals, eigVects = np.linalg.eig(np.mat(covMat))
eigValInd = np.argsort(eigVals)  # sort, sort goes smallest to largest
eigValInd = eigValInd[::-1]  # reverse
sortedEigVals = eigVals[eigValInd]
total = sum(sortedEigVals)
varPercentage = sortedEigVals / total * 100
# 計算主成分方差
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(range(1, 21), varPercentage[:20], marker='^')
plt.xlabel('Principal Component Number')
plt.ylabel('Percentage of Variance')
plt.show()

結果：
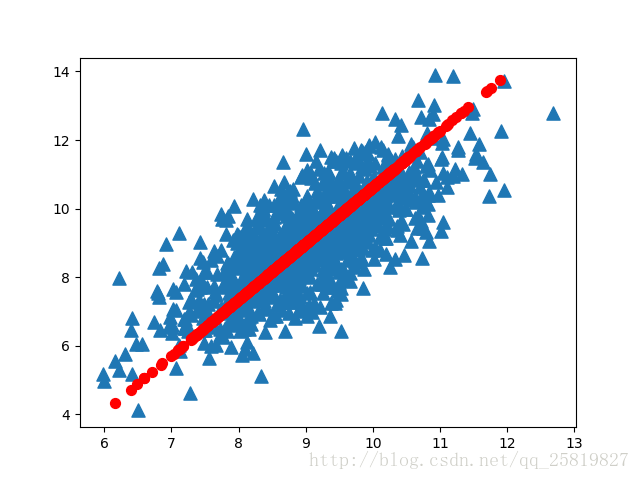
藍色三角形為原始資料，紅色圓為資料的主方向，可以看到PCA演算法很好地找到了資料的主方向

人臉識別：

att_faces中含有40張臉，每張臉10張92*112畫素灰度照片的資料集

這裡以att_faces資料集為例：

import os
import operator
from numpy import *
import matplotlib.pyplot as plt
import cv2

# define PCA
def pca(data,k):
    data = float32(mat(data))
    rows,cols = data.shape#取大小
    data_mean = mean(data,0)
    data_mean_all = tile(data_mean,(rows,1))
    Z = data - data_mean_all#中心化
    T1 = Z*Z.T #計算樣本的協方差
    D,V = linalg.eig(T1) #特徵值與特徵向量
    V1 = V[:,0:k]#取前k個特徵向量
    V1 = Z.T*V1
    for i in range(k): #特徵向量歸一化
        L = linalg.norm(V1[:,i])
        V1[:,i] = V1[:,i]/L

    data_new = Z*V1 # 降維後的資料
    return data_new,data_mean,V1#訓練結果

#covert image to vector
def img2vector(filename):
    img = cv2.imread(filename,0) #讀取圖片
    rows,cols = img.shape
    imgVector = zeros((1,rows*cols)) #create a none vectore:to raise speed
    imgVector = reshape(img,(1,rows*cols)) #change img from 2D to 1D
    return imgVector

#load dataSet
def loadDataSet(k):  #choose k(0-10) people as traintest for everyone
    ##step 1:Getting data set
    print ("--Getting data set---")
    #note to use '/'  not '\'
    dataSetDir = 'att_faces/orl_faces'
    #讀取資料夾
    choose = random.permutation(10)+1 #隨機排序1-10 (0-9）+1
    train_face = zeros((40*k,112*92))
    train_face_number = zeros(40*k)
    test_face = zeros((40*(10-k),112*92))
    test_face_number = zeros(40*(10-k))
    for i in range(40): #40 sample people
        people_num = i+1
        for j in range(10): #everyone has 10 different face
            if j < k:
                filename = dataSetDir+'/s'+str(people_num)+'/'+str(choose[j])+'.pgm'
                img = img2vector(filename)
                train_face[i*k+j,:] = img
                train_face_number[i*k+j] = people_num
            else:
                filename = dataSetDir+'/s'+str(people_num)+'/'+str(choose[j])+'.pgm'
                img = img2vector(filename)
                test_face[i*(10-k)+(j-k),:] = img
                test_face_number[i*(10-k)+(j-k)] = people_num

    return train_face,train_face_number,test_face,test_face_number

# calculate the accuracy of the test_face
def facefind():
    # Getting data set
    train_face,train_face_number,test_face,test_face_number = loadDataSet(4)
    # PCA training to train_face
    data_train_new,data_mean,V = pca(train_face,40)
    num_train = data_train_new.shape[0]
    num_test = test_face.shape[0]
    temp_face = test_face - tile(data_mean,(num_test,1))
    data_test_new = temp_face*V #對測試集進行降維
    data_test_new = array(data_test_new) # mat change to array
    data_train_new = array(data_train_new)
    true_num = 0
    for i in range(num_test):
        testFace = data_test_new[i,:]
        diffMat = data_train_new - tile(testFace,(num_train,1))
        sqDiffMat = diffMat**2
        sqDistances = sqDiffMat.sum(axis=1)
        sortedDistIndicies = sqDistances.argsort()
        indexMin = sortedDistIndicies[0]
        if train_face_number[indexMin] == test_face_number[i]:
            true_num += 1

    accuracy = float(true_num)/num_test
    print ('The classify accuracy is: %.2f%%'%(accuracy * 100))

def main():
    facefind()

if __name__=='__main__':
    main()

結果：

由於每次選擇訓練的圖片是隨機的，隨後的準確率也是會變化的，當提高低維空間的維度時能提高準確率
程式碼資源