排序算法系列:歸併排序演算法
概述
上一篇我們說了一個非常簡單的排序演算法——選擇排序。其複雜程式完全是冒泡級的,甚至比冒泡還要簡單。今天要說的是一個相對比較複雜的排序演算法——歸併排序。複雜的原因不僅在於歸併排序分成了兩個部分進行解決問題,而是在於,你需要一些演算法的思想支撐。
歸併排序和之前我寫的一篇部落格《大資料演算法:對5億資料進行排序》有很多相似的地方,如果你感興趣,也可以去看看那一篇部落格。
版權說明
目錄
弱分治歸併
歸併的核心演算法就是上面提到過的兩個過程。分別是分治與合併。合併都好理解,那麼什麼是分治呢?下面就來逐一說明一下。
演算法原理
弱分治歸併排序演算法中,我們主要說的是合併,因為這裡的分治更像是分組。
背景
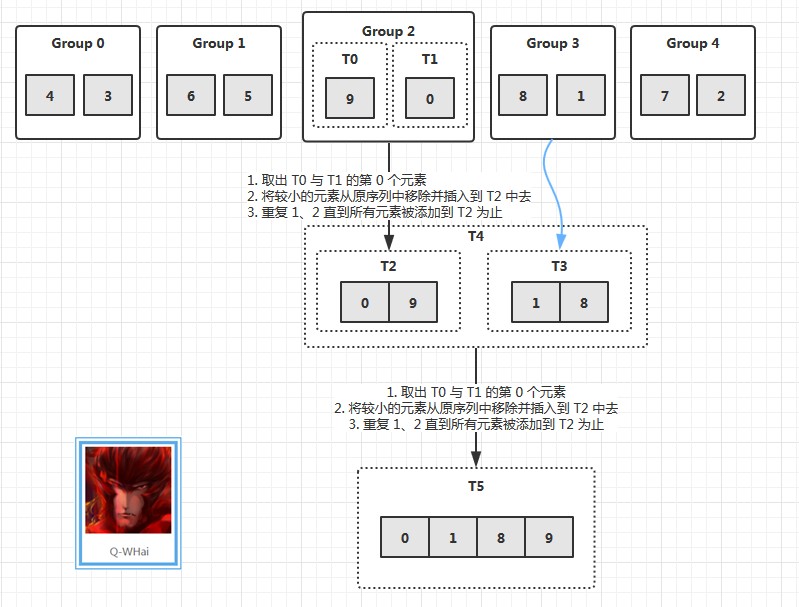
假設我們有序列 T0 = [ 4, 3, 6, 5, 9, 0, 8, 1, 7, 2 ]
那麼,在一開始,我們的序列就被分成了 10 組,每一組的元素個數為 1。
合併
先說合並吧,因為它簡單一些。在合併模組中,需要傳入兩個序列引數,並保證待合併的兩個序列本身已經有序。現在我們假設待合併的兩個有序序列分別為:
t0 = [ 0, 9 ]
t1 = [ 1, 8 ]
看到這兩個序列讓人很自然地想到,只要依次取 t0 和 t1 中的最小的元素即可。並且最小的元素就是第一個元素。當我們取完 t0
合併過程圖解
下面是合併的核心程式碼
// 合併的核心模組
private void merge(int[] array, int low, int mid, int hight) {
if (low >= hight) {
return;
}
int[] auxArray = new int[hight - low + 1 分治
我想大部分人應該不會被合併邏輯給難住吧。只是分治的邏輯會有一些麻煩,麻煩不是在於分治思想的麻煩,而是分治過程的邏輯程式碼不好編寫。正因為如此,所以我們在前面先講解弱分治歸併,這樣在下面看到強分治歸併的分治邏輯時,你才不會毫無頭緒。在上面也說了,弱分治並歸更像是一個分組合並的過程。也就是一開始就有很多組,然後慢慢合併,在合併的過程中分組減少了,合併後的有序陣列變大了,直至只有一個數組為止。
在合併中最容易想到的是兩兩合併。所以在分組後,就兩兩進行合併。只要我們能準確地取到相鄰的兩個序列就可以進行合併了。
下面是程式碼實現
// 對陣列進行分組的核心模組
private void sortCore(int[] array) {
int length = array.length;
int groupSize = 1;
while(groupSize < length) {
for (int i = 0; i < length; i += (groupSize * 2)) {
int low = i;
int hight = Math.min(i + groupSize * 2 - 1, length - 1);
int middle = low + groupSize - 1;
merge(array, low, middle >= hight ? (low + hight) / 2 : middle, hight);
}
groupSize *= 2;
}
// 對分組中的奇數情況進行另外處理
if (groupSize / 2 < length) {
int low = 0;
int hight = length - 1;
merge(array, low, groupSize / 2 - 1, hight);
}
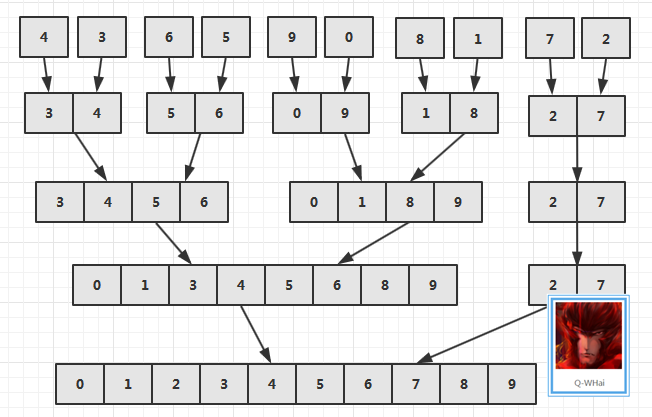
}在上面的程式碼中,可以看到最後有一個奇數分組的邏輯處理。這是怎麼回事呢?很好理解,假設,現在給你 (2n + 1) 個分組的有序序列,按照前面講的兩兩合併,那麼只能合併前面的 2n 個序列,第 (2n + 1) 個序列找到可合併的物件。處理的方式就是把它保留到最後與迭代後的有序序列進行合併即可。這一點從下面的圖解中也可以獲知。
排序過程圖解
演算法實現
/**
* <p>
* 歸併排序演算法
* </p>
* 2016年1月20日
*
* @author <a href="http://weibo.com/u/5131020927">Q-WHai</a>
* @see <a href="http://blog.csdn.net/lemon_tree12138">http://blog.csdn.net/lemon_tree12138</a>
* @version 0.1.1
*/
public class MergeSort implements Sortable {
@Override
public int[] sort(int[] array) {
if (array == null) {
return null;
}
sortCore(array);
return array;
}
// 對陣列進行分組的核心模組
private void sortCore(int[] array) {
( ... 此處省略上面分治的邏輯 ... )
}
// 合併的核心模組
private void merge(int[] array, int low, int mid, int hight) {
( ... 此處省略上面合併的邏輯 ... )
}
}強分治歸併
演算法原理
強分治歸併相比弱分治歸併的不同點在於,強分治歸併有沒在一開始就對陣列 T0 進行分組,而是通過程式來對 T0 進行分組,現在可以看一張強分治歸併排序演算法的過程圖感受一下。
合併
不管弱分治歸併還是強分治歸併,其合併的邏輯都是一樣的。大家可以自行參考上面的邏輯,這裡就不廢話了。
分治
從上面的排序過程圖中也可以發現,強分治歸併需要將原陣列先劃分成小陣列。首先將一個大陣列分割成兩個小陣列,再將兩個小陣列分割成四個小陣列,如此往復。字裡行間都表明了,這裡需要進行遞迴操作。
強分治歸併演算法的分治部分邏輯程式碼:
/**
* 對陣列進行分組的核心模組
*
* @param array
* 待排序陣列
* @param start
* 開始位置
* @param end
* 結束位置(end 為 陣列可達下標)
*/
private void sortCore(int[] array, int start, int end) {
if (start == end) {
return;
} else {
int middle = (start + end) / 2;
sortCore(array, start, middle);
sortCore(array, middle + 1, end);
merge(array, start, middle, end);
}
}總結
演算法複雜度
| 排序方法 | 時間複雜度 | 空間複雜度 | 穩定性 | 複雜性 | ||
| 平均情況 | 最壞情況 | 最好情況 | ||||
| 歸併排序 | O( |
O( |
O( |
O( |
穩定 | 較複雜 |
強弱分治歸併的比較
需要比較的主是程式碼邏輯複雜度和執行效率
這裡我們用了一個數組為: int[] array = { 4, 3, 6, 5, 9, 0, 8, 1, 7, 2 };
迴圈執行 1000000 次後得到如下結果:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
MergeSort 用時:509 ms
-------------------------------------
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
MergeImproveSort 用時:374 ms| 演算法名稱 | 程式碼邏輯複雜度 | 執行效率 | bigger 值 |
|---|---|---|---|
| 弱分治歸併 | 簡單 | 低 | 低 |
| 強分治歸併 | 複雜 | 高 | 高 |
所以,如果想要執行效率高一些或是刷刷 bigger 值,那麼請使用強分治歸併排序演算法。
Ref
- 《大話資料結構》