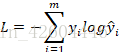吳恩達深度學習第二課第三週作業及學習心得體會 ——softmax、batchnorm
寫在前面
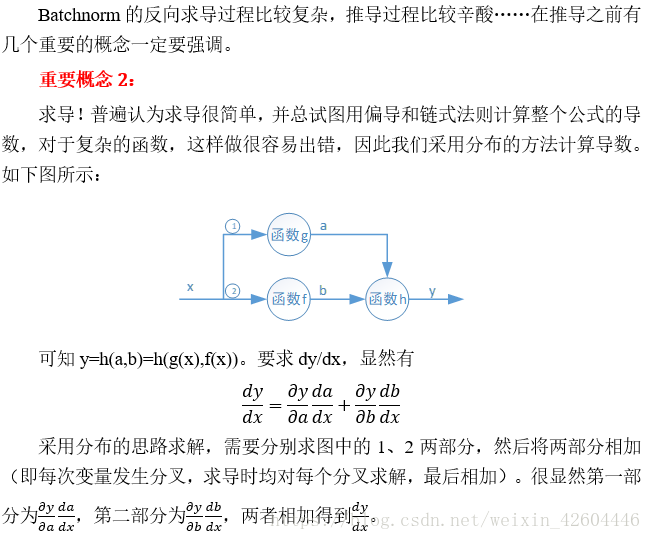
本週課程用了兩週完成,因為課程讓用tensorflow實現,編碼時還是更希望自己手寫程式碼實現,而在實現過程中,低估了batchnorm反向計算的難度,導致演算法出現各種bug,開始是維度上的bug導致程式碼無法執行,等程式碼可以執行時,訓練神經網路的時候成本又總會發散,於是靜下心來把整個運算的前向和反向過程認真推導了好幾遍,期間參考網上一些資料,但感覺都沒有把問題真正說清楚,連續三天的推導後,才找到了問題的本質,現將自己寫的程式碼彙總如下。
softmax
概念
softmax相對來說比較簡單。其用於處理多元分類問題,而之前學習迴歸時就在思考怎麼解決多元分類問題,並無師自通的實現了onehot編碼和hardmax(也是學習softmax時才明白之前實現的是onehot編碼和hardmax迴歸)……
迴歸模型是Logistic迴歸模型在多分類問題上的推廣,在多分類問題中,輸出y的值不再是一個數,而是一個多維列向量,有多少種分類是就有多少維數。啟用函式使用的是softmax函式:
損失函式變為:
其反向傳播求導公式即為:。注意該公式指的是
(程式碼中寫為dZ),而不是
!
程式碼
庫:
import numpy as np
import matplotlib.pyplot as plt訓練集資料程式碼:
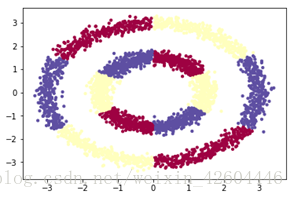
'''**********************************************************************''' #產生資料 def gendata(): np.random.seed(1) m = 3600 #樣本數 N = int(m/2) #分為兩類 D = 2 #樣本的特徵數或維度 X = np.zeros((m,D)) #初始化樣本座標 y = np.zeros((m,1)) #初始化樣本標籤 Y = np.zeros((m,3)) #初始化樣本標籤 a = 1.5 #基礎半徑 for j in range(12): if j<6: ix = range((m//12)*j, (m//12)*(j+1)) t = np.linspace((3.14/3)*j+0.01, (3.14/3)*(j+1)-0.01, m//12) #theta角度 r = a + np.random.randn(m//12)*0.15 #radius半徑 X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成座標點 y[ix] = j%3 ''' if j%3==0: Y[ix] = [1,0,0] if j%3==1: Y[ix] = [0,1,0] if j%3==2: Y[ix] = [0,0,1] ''' else: ix = range((m//12)*j, (m//12)*(j+1)) t = np.linspace((3.14/3)*j+0.01, (3.14/3)*(j+1)-0.01, m//12) #theta角度 r = a*2 + np.random.randn(m//12)*0.15 #radius半徑 X[ix] = np.c_[r*np.sin(t), r*np.cos(t)] #生成座標點 y[ix] = (j+1)%3 ''' if j%3==0: Y[ix] = [0,1,0] if j%3==1: Y[ix] = [0,0,1] if j%3==2: Y[ix] = [1,0,0] ''' Y = np.eye(3)[np.int32(y).reshape(-1)] #該語句實現的功能與上面註釋部分相同 return X.T,Y.T,y.T
繪出圖形如下:
單次前向函式,刪除sigmoid函式(可以不刪除……),增加softmax函式,注意np.sum(np.exp(Z),axis=0),是對np.exp(Z)求和,axis=0表示按行求和,計算出來的向量應該是(1,m),即對每個樣本列裡的元素求和;
'''**********************************************************************''' #單次前向運算 def single_forward(A_pre, W, b, mode): Z = np.dot(W, A_pre) + b #根據上一層的輸出A_pre,以及本層的W b計算本層的Z if mode=='softmax': #根據所選定的啟用函式計算本層的輸出 A = np.exp(Z)/np.sum(np.exp(Z),axis=0) #np.sum(np.exp(Z),axis=0),是對np.exp(Z)求和,axis=0表示按行求和,計算出來的向量應該是(1,m) if mode=='ReLU': A = (Z+abs(Z))/2 if mode=='tanh': A = np.tanh(Z) cache = {'A_pre':A_pre, 'W':W, 'b':b, 'Z':Z, 'A':A} return cache
前向傳播函式中第L層,呼叫sigmoid改為呼叫softmax;
'''**********************************************************************'''
#前向傳播函式
def prop_forward(X, parameters,lambd):
caches = []
L = len(parameters)//2
for l in range(1,L+1): #l從1到L,呼叫L次前向運算
W = parameters['W'+str(l)]
b = parameters['b'+str(l)]
if l==1: #第一次運算時,A_pre=X
A_pre = X
L2_SUM = 0
else:
A_pre = cache['A']
L2_SUM = L2_SUM + 0.5*lambd*np.sum(W*W)
if l==L: #最後一次運算時,啟用函式為sigmoid
mode = 'softmax'
else:
mode = 'tanh'
cache = single_forward(A_pre, W, b, mode)
caches.append(cache)
AL = caches[L-1]['A']
return AL, caches, L2_SUM單次後向函式,對第L層的softmax函式求導,直接等於A-Y,無需計算dA;
'''**********************************************************************'''
#單次後向運算
def single_backward(Y, dA, cache, mode, lambd):
A_pre = cache['A_pre']
W = cache['W']
b = cache['b']
A = cache['A']
m = A_pre.shape[1]
if mode=='softmax': #根據本層啟用函式計算本層的dZ
dZ = (A-Y) #softmax函式 dL/dZ = AL-Y,不必再通過dL/dAL計算來計算dL/dZ
if mode=='ReLU':
dZ = dA #ReLU函式:A>=0,dZ=dA
dZ[A<0] = 0
if mode=='tanh':
dZ = dA*(1-A**2) #tanh函式: dZ=dA*(1-A*A)
#根據dZ, A_pre, W計算本層梯度dW db,同時計算dA_pre供前一層反向運算使用
grad = {'dW':1.0/m*np.dot(dZ, A_pre.T) + lambd/m*W,
'db':1.0/m*np.sum(dZ, axis=1, keepdims=True),
'dA_pre':np.dot(W.T, dZ)}
return grad後向傳播函式中,最後一層也改為呼叫softmax函式,且該層dA=-Y/AL(這句程式碼在該程式中沒用,因為計算dZ時沒有用到dA);
'''**********************************************************************'''
#後向傳播函式
def prop_backward(AL, Y, caches, lambd):
grads = {} #注意:使用append時應初始化為[],否則應為{}
L = len(caches)
for l in reversed(range(L)): #計算梯度
if l==L-1: #計算dAL
dA = -Y/AL #該步運算沒有實際用途,因為softmax函式 dL/dZ = AL-Y,不必再計算dL/dAL
mode = 'softmax'
else:
dA = grad['dA_pre']
mode = 'tanh'
grad = single_backward(Y, dA, caches[l], mode, lambd)
grads['dW'+str(l+1)] = grad['dW']
grads['db'+str(l+1)] = grad['db']
return grads預測函式,比較簡單粗暴地用了np.round。
'''**********************************************************************'''
#預測函式
def predict(X,parameters,lambd):
AL, caches, L2_SUM = prop_forward(X, parameters,lambd)
prediction = np.round(AL)
return prediction
同時還使用了L2正則化、minibatch、Adam。
試驗效果
試驗程式碼如下
X,Y,y = gendata()
x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),np.arange(y_min, y_max, 0.01)) #將二維平面以0.01*0.01的間隔散開,xx為每個點的橫座標,yy為每個點的縱座標
zz = np.array([xx.ravel(), yy.ravel()]).T #zz為每個點的橫縱座標,其行數為總點數,列數為特徵數,即維度
layer_dims = [2,288,144,72,36,18,6,3]
steps = 100 #訓練次數
rate = 0.01 #訓練步長
print_flag = True #列印cost標識
lambd = 0 #L2正則化係數,為0時不進行正則化
batch_size = 600 #mini_batch_size,為1時即為隨機梯度下降,為X.shape[1]時即不分批
parameters,costs = NN_model(X, Y, layer_dims, steps, rate, lambd, batch_size, print_flag)
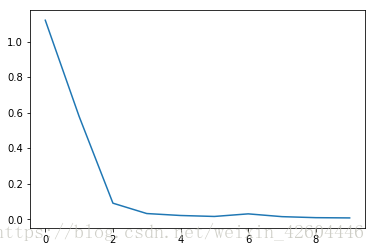
plt.plot(costs)
prediction = predict(X,parameters,lambd) #根據訓練出來的神經網路,對X進行預測
p_NN = np.mean(prediction==Y) #計算預測的準確率
print('\nL層神經網路的準確率為:%f'%p_NN)
Z_NN_predict = predict(zz.T,parameters,lambd) #通過神經網路對每個點進行預測
Z_NN = np.zeros(Z_NN_predict.shape[1])
for i in range(Z_NN_predict.shape[1]):
if Z_NN_predict[0,i]==1:
Z_NN[i] = 0
if Z_NN_predict[1,i]==1:
Z_NN[i] = 1
if Z_NN_predict[2,i]==1:
Z_NN[i] = 2
Z_NN = Z_NN.reshape(xx.shape)
plt.figure(2)
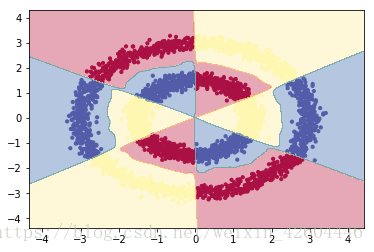
plt.scatter(X[0, :], X[1, :], c=np.squeeze(y), s=10, cmap=plt.cm.Spectral)
plt.contourf(xx, yy, Z_NN, alpha=0.4,cmap=plt.cm.Spectral) #繪製等高線
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.show()試驗效果如下:
Batchnorm
概念
批標準化(Batch Normalization,BN)和之前的資料集標準化類似,是將分散的資料進行統一的一種做法。具有統一規格的資料,能讓機器更容易學習到資料中的規律。
對於一個神經網路,前面權重值的不斷變化就會帶來後面權重值的不斷變化,批標準化減緩了隱藏層權重分佈變化的程度。採用批標準化之後,儘管每一層的z還是在不斷變化,但是它們的均值和方差將基本保持不變,這就使得後面的資料及資料分佈更加穩定,減少了前面層與後面層的耦合,使得每一層不過多依賴前面的網路層,最終加快整個神經網路的訓練。
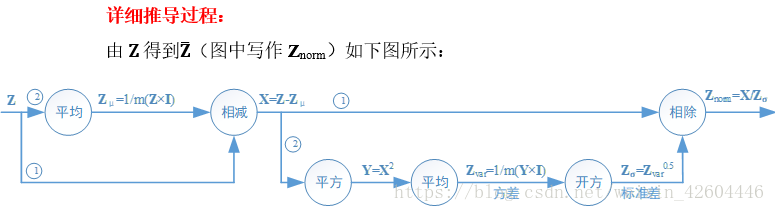
正向過程
(本來錄入完了,csdn對 word的相容實在太差……中間報了幾次伺服器錯誤,我也沒理會,結果發現,辛辛苦苦改的博文木有了!!!哎,我還是直接從筆記裡截圖過來吧……)
反向過程
import numpy as np
np.random.seed(0)
Z = np.random.randn(2,100) #2*100的矩陣Z,2個特徵,100個樣本
dZnorm = np.random.randn(2,100)*0.5 #2*100的矩陣dZnorm,2個特徵,100個樣本
nl = Z.shape[0]
m = Z.shape[1]
#方法1
mu = np.mean(Z,axis=1).reshape(nl,1) #用np.mean直接計算平均值,2*1的矩陣
var = np.var(Z,axis=1).reshape(nl,1) #用np.var直接計算方差,2*1的矩陣
sigma = np.sqrt(var) #方差開方得到標準差,2*1的矩陣
temp1 = dZnorm/sigma #用np.sum的方法計算dZ
temp2 = -1.0 / m / sigma * np.sum(dZnorm,axis=1).reshape(nl,1)
temp3 = -1.0 / m / (sigma**3) * (Z-mu) * np.sum(dZnorm*(Z-mu),axis=1).reshape(nl,1)
dZ_1 = temp1+temp2+temp3
#方法2
I = np.ones((m,m))
Z_mu = 1.0/m * np.dot(Z,I) #用乘以全1矩陣的方法計算平均值,2*100的矩陣
Z_var = 1.0/m*np.dot((Z-Z_mu)**2,I) #用乘以全1矩陣的方法計算方差,2*100的矩陣
Z_sigma = np.sqrt(Z_var) #方差開方得到標準差,2*100的矩陣
temp4 = dZnorm/Z_sigma #用乘以全1矩陣的方法計算dZ
temp5 = -1.0 / m / Z_sigma * np.dot(dZnorm,I)
temp6 = -1.0 / m / (Z_sigma**3) * (Z-Z_mu) * np.dot(dZnorm*(Z-Z_mu),I)
dZ_2 = temp4+temp5+temp6
#比較
print(np.round(temp1-temp4))
print(np.round(temp2-temp5))
print(np.round(temp3-temp6))
print(np.round(dZ_1-dZ_2))
執行證明兩者效果相同!
Batchnorm實現程式碼
在保留上面程式碼的基礎上更改,程式碼更改如下:
初始化引數函式中增加標準差向量D,相應初始化adam函式以及更新引數中都要增加對應向量:
'''**********************************************************************'''
#初始化引數
def init_para(layer_dims):
L = len(layer_dims) #L為總層數
np.random.seed(L)
parameters = {}
for l in range(1,L): #初始化W1~WL,b1~bL
n1 = layer_dims[l]
n2 = layer_dims[l-1]
if l==(L-1): #最後一層用softmax函式,初始化時應為1/n2
a = 1.0
else: #其他層用ReLU函式,初始化時應為2/n2
a = 2.0
parameters['W'+str(l)] = np.random.randn(n1, n2) * np.sqrt(a/n2)
parameters['D'+str(l)] = np.ones((n1, 1))
parameters['b'+str(l)] = np.zeros((n1, 1))
return parameters單次前向函式(注意單個樣本時,要特殊處理,原因可在除錯時自行分析):
'''**********************************************************************'''
#單次前向運算
def single_forward(A_pre, W, D, b, mode):
epsilon = 1e-8
Z = np.dot(W, A_pre) #根據上一層的輸出A_pre,以及本層的W b計算本層的Z
if Z.shape[1] != 1: #表示不是再進行單個樣本運算
Z_mu = np.mean(Z, axis = 1).reshape(Z.shape[0],1) #reshape(Z.shape[0],1)或者keepdims=True都可以,目的是讓其從向量變為矩陣(列數為1)
Z_var = np.var(Z, axis = 1).reshape(Z.shape[0],1)+epsilon #epsilon防止Z_norm計算時除以0,在這裡加,還方便了反向求導運算
Z_norm = (Z - Z_mu)/(np.sqrt(Z_var))
else: #表示在進行單個樣本的運算
Z_mu = 0 #令平均值為0
Z_var = 1 #令方差為1
Z_norm = Z #將Z直接賦給其標準化的值
Z_bn = D * Z_norm + b
if mode=='softmax': #根據所選定的啟用函式計算本層的輸出
A = np.exp(Z_bn)/np.sum(np.exp(Z_bn),axis=0)
if mode=='ReLU':
A = (Z_bn+abs(Z_bn))/2
if mode=='tanh':
A = np.tanh(Z_bn)
cache = {'A_pre':A_pre,
'W':W,
'D':D,
'b':b,
'Z':Z,
'Z_mu':Z_mu,
'Z_var':Z_var,
'Z_norm':Z_norm,
'Z_bn':Z_bn,
'A':A}
return cache單次後向函式
'''**********************************************************************'''
#單次後向運算
def single_backward(Y, dA, cache, mode, lambd):
A_pre = cache['A_pre']
W = cache['W']
D = cache['D']
b = cache['b']
A = cache['A']
Z = cache['Z']
Z_mu = cache['Z_mu']
Z_var = cache['Z_var']
Z_sigma = np.sqrt(Z_var)
Z_norm = cache['Z_norm']
m = A_pre.shape[1]
if mode=='softmax': #根據本層啟用函式計算本層的dZ
dZ_bn = (A-Y) #softmax函式 dL/dZ_bn = AL-Y,不必再通過dL/dAL計算來計算dL/dZ_bn
if mode=='ReLU':
dZ_bn = dA #ReLU函式:A>=0,dZ_bn=dA
dZ_bn[A<0] = 0 #ReLU函式:A<0, dZ_bn=0
if mode=='tanh':
dZ_bn = dA*(1-A**2) #tanh函式: dZ_bn=dA*(1-A*A)
dD = 1.0/m*np.sum(dZ_bn*Z_norm, axis=1, keepdims=True)
db = 1.0/m*np.sum(dZ_bn, axis=1, keepdims=True)
dZ1 = D*dZ_bn/Z_sigma #用np.sum的方法計算dZ
dZ2 = -1.0 / m / Z_sigma * np.sum(D*dZ_bn,axis=1, keepdims=True)
dZ3 = -1.0 / m / (Z_sigma**3) * (Z-Z_mu) * np.sum(D*dZ_bn*(Z-Z_mu),axis=1, keepdims=True)
dZ = dZ1 + dZ2 + dZ3
dW = 1.0/m*np.dot(dZ, A_pre.T) + lambd/m*W
dA_pre = np.dot(W.T, dZ)
#根據dZ, A_pre, W計算本層梯度dW db,同時計算dA_pre供前一層反向運算使用
grad = {'dW':dW,
'dD':dD,
'db':db,
'dA_pre':dA_pre}
return grad
實施效果
讀取課程的手勢圖形檔案,建立神經網路,引數如下:
layer_dims = [X_train.shape[0],24,12,6]
steps = 200 #訓練次數
rate = 0.002 #訓練步長
print_flag = True #列印cost標識
lambd = 0.1 #L2正則化係數,為0時不進行正則化
batch_size = 128 #mini_batch_size,為1時即為隨機梯度下降,為X.shape[1]時即不分批對手勢訓練集和測試集的預測準確率分別為1,0.951。
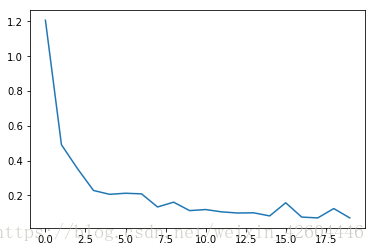
成本下降過程如下(每10次全樣本訓練記錄一次成本):
總結
推導過程中走了不少彎路,csdn上很多部落格也說的不明不白,好在想到了batchnorm中的平均運算可以用矩陣乘法表示,後面的推導就豁然開朗。
後續還需要認真學習tensorflow,雖然用了tensorflow自帶的softmax,但並沒有用tensorflow自帶的batchnorm。加油!!!
附
作業的原始碼在我的資源中,可用spyder直接執行,感興趣的朋友可以下載。