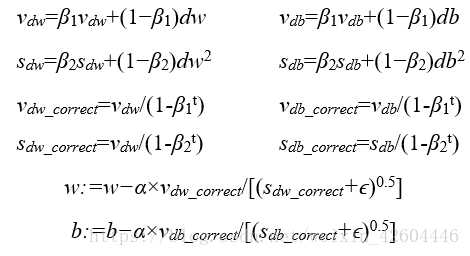吳恩達深度學習第二課第二週作業及學習心得體會——minibatch、動量梯度下降、adam
概述
學習課程後,在L2正則化程式碼的基礎上完成該周作業,現將心得體會記錄如下。
Mini-batch梯度下降
概念
對m個訓練樣本,每次採用t(1<t<m)個樣本進行迭代更新。
具體過程為:將特徵X分為T個batch,每個batch的樣本數為t(最後一個batch樣本數不一定為t)。相應的將標籤Y也如此分為T個batch。然後在每次訓練時,原本是對所有樣本進行一次訓練;該演算法則是對T個batch都進行訓練,因此每次訓練完所有樣本,實際上都進行了T次訓練。
注意為了保證沒批樣本的一致性,在分批前應對樣本進行序號進行洗牌,隨機重新分配樣本的序號。
實際實現時,通常將每個batch的樣本數t設定為2的整數次冪(64,128,256…)這是為了節省計算機記憶體。
理解
不用這種方法時:
執行一次梯度下降,向量化運算需要處理所有樣本,耗時長;
當處理一次所有樣本時,執行了一次梯度下降。
採用批量梯度下降演算法時:
執行一次梯度下降,向量化運算需要處理t個樣本,耗時短;
當處理一次所有樣本時,執行了T次梯度下降。
因此可知,當樣本量大時,其優點顯而易見!假設有1000000個樣本,如果不採用批量梯度下降法,用了20000次訓練(即20000次梯度下降),才得到合適的網路;如果採用批量梯度下降法,令t=1000(則T=1000000/1000=1000),則每次訓練完所有樣本,實際上已經執行了1000次梯度下降,如果樣本在分批時進行了隨機排序處理,那麼在上面的假設條件下,只需要對所有樣本進行20次訓練(梯度下降次數=20×1000=20000),就可以找到合適的網路。其效率明顯提高。
特殊情況
當t=m(總樣本數)時,等於沒有分批,稱作批梯度下降。
優點:最小化所有訓練樣本的損失函式,得到全域性最優解;易於並行實現。
缺點:當樣本數目很多時,訓練過程會很慢。
當t=1時,每次只對一個樣本進行訓練,稱作隨機梯度下降。
優點:訓練速度快。
缺點:最小化每條樣本的損失函式,最終的結果往往是在全域性最優解附近,不是全域性最優;不易於並行實現。
程式碼更改
程式碼更改如下:
- 增加分批函式:
def random_batch(X, Y, batch_size): batchs = [] np.random.seed(0) m = X.shape[1] random_index = list(np.random.permutation(m)) #random_index為一維陣列,大小0~m-1,順序隨機 shuffled_X = X[:,random_index] #對X按照random_index的順序重新排序(洗牌) shuffled_Y = Y[:,random_index] #對Y按照random_index的順序重新排序(洗牌) num_batchs = int(np.floor(m/batch_size)) #計算批數 for k in range(0,num_batchs): #將洗牌後的X,Y分成num_batchs個batch start = k * batch_size end = (k+1) * batch_size batch_X = shuffled_X[:,start:end] batch_Y = shuffled_Y[:,start:end] batch = (batch_X, batch_Y) batchs.append(batch) if m % batch_size != 0: #如果總樣本數不能整分,將剩餘樣本組成最後一個batch start = (k+1) * batch_size end = m batch_X = shuffled_X[:,start:end] batch_Y = shuffled_Y[:,start:end] batch = (batch_X, batch_Y) batchs.append(batch) return batchs
- 模型函式:
def NN_model(X, Y, layer_dims, learning_steps, learning_rate, lambd, batch_size, print_flag):
costs=[]
batchs = random_batch(X, Y, batch_size) #將樣本以batch_size分為一組batch
K = len(batchs) #batchs長度
parameters = init_para(layer_dims) #初始化引數
for i in range(0, learning_steps): #進行learning_steps次訓練
for k in range(0, K):
x = batchs[k][0] #第k個batch的特徵
y = batchs[k][1] #第k個batch的標籤
AL, caches, L2_SUM = prop_forward(x, parameters,lambd) #前向傳播,計算A1~AL
cost = compute_cost(AL,y,L2_SUM) #計算成本
grads = prop_backward(AL, y, caches, lambd) #反向傳播,計算dW1~dWL,db1~dbL
parameters = update_para(parameters, grads, learning_rate) #更新引數
if print_flag==True and i%100==0:
print('cost at %i steps:%f'%(i, cost))
costs.append(cost)
return parameters,costs
實施效果
總樣本數為5000,引數如下:
layer_dims = [X.shape[0],4,2,1] #NN的規模
steps = 1000 #訓練次數
rate = 0.1 #訓練步長
print_flag = True #列印cost標識
lambd = 0 #L2正則化係數,為0時不進行正則化
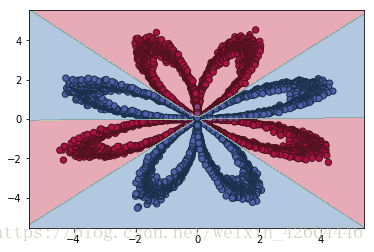
令batch_size=m,效果如下。
令batch_size=512,效果如下。
可見分批處理後,收斂速度明顯變快!
動量梯度下降
概念
動量梯度下降(Gradient Descent with Momentum)是計算梯度的指數加權平均數,並利用該值來更新引數值。具體過程為:
其中的動量衰減引數β一般取0.9。
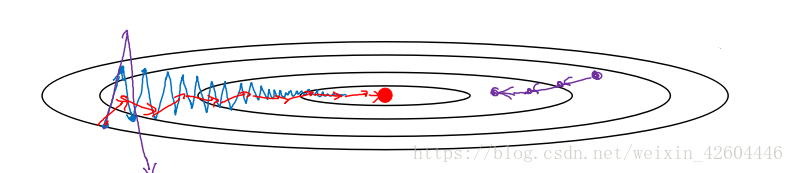
進行一般的梯度下降將會得到圖中的藍色曲線,而使用Momentum梯度下降時,通過累加減少了抵達最小值路徑上的擺動,加快了收斂,得到圖中紅色的曲線。
當前後梯度方向一致時,Momentum梯度下降能夠加速學習;前後梯度方向不一致時,Momentum梯度下降能夠抑制震盪。
程式碼更改
在保留上面程式碼的基礎上更改,程式碼更改如下:
增加初始化函式:
def init_v(parameters):
L = len(parameters)//2 #NN層數
v = {}
for l in range(L):
v["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
return v更新引數函式:
def update_para(parameters, grads, v, learning_rate):
L = len(parameters)//2
beta = 0.9 #動量梯度下降係數(梯度的指數加權平均係數)
for l in range(L):
v["dW" + str(l+1)] = beta*v["dW" + str(l+1)] + (1- beta)*grads["dW" + str(l+1)]
v["db" + str(l+1)] = beta*v["db" + str(l+1)] + (1- beta)*grads["db" + str(l+1)]
parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v["dW" + str(l+1)]
parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v["db" + str(l+1)]
return parameters, v實施效果
總樣本數為5000,引數如下:
layer_dims = [X.shape[0],4,2,1] #NN的規模
steps = 1000 #訓練次數
rate = 0.1 #訓練步長
print_flag = True #列印cost標識
lambd = 0 #L2正則化係數,為0時不進行正則化
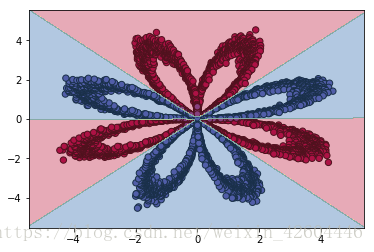
batch_size = 512 #mini_batch_size,為1時即為隨機梯度下降,為X.shape[1]時即不分批令beta=0.9,預測準確率為0.975200,效果如下。
令beta=0,預測準確率為0.970600,效果如下。
可能是樣本過於簡單,使用動量梯度下降時除了準確率略微提高,並沒有明顯變化。
Adam優化演算法
概念
Adam(Adaptive Moment Estimation,自適應矩估計)優化演算法適用於很多不同的深度學習網路結構,它本質上是將Momentum梯度下降和RMSProp演算法結合起來。具體過程為:
其中的學習率α需要進行調參,超引數β1被稱為第一階矩,一般取0.9,β2被稱為第二階矩,一般取0.999,ϵ一般取10^−8。
程式碼更改
在2.4程式碼的基礎上更改,程式碼更改如下:
增加初始化函式:
def init_adam(parameters):
L = len(parameters)//2 #NN層數
v = {}
s = {}
for l in range(L):
v["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
s["dW" + str(l+1)] = np.zeros(parameters['W' + str(l+1)].shape)
s["db" + str(l+1)] = np.zeros(parameters['b' + str(l+1)].shape)
return v,s更新引數函式:
def update_para(parameters, grads, v, s, learning_rate):
L = len(parameters)//2
v_corrected = {}
s_corrected = {}
t=2 #t不能為0!
beta1=0.9
beta2=0.999
epsilon=1e-8
for l in range(L):
v["dW" + str(l+1)] = beta1*v["dW" + str(l+1)] + (1- beta1)*grads["dW" + str(l+1)]
v["db" + str(l+1)] = beta1*v["db" + str(l+1)] + (1- beta1)*grads["db" + str(l+1)]
v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)]/(1-beta1**t)
v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/(1-beta1**t)
s["dW" + str(l+1)] = beta2*s["dW" + str(l+1)] + (1- beta2)*(grads['dW' + str(l + 1)]**2)
s["db" + str(l+1)] = beta2*s["db" + str(l+1)] + (1- beta2)*(grads['db' + str(l + 1)]**2)
s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/(1-beta2**t)
s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-beta2**t)
parameters['W' + str(l+1)] = parameters['W' + str(l+1)] - learning_rate*v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)
parameters['b' + str(l+1)] = parameters['b' + str(l+1)] - learning_rate*v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)
return parameters, v, s實施效果
總樣本數為5000。採用adam演算法,引數如下。
layer_dims = [X.shape[0],4,2,1] #NN的規模
steps = 100 #訓練次數
rate = 0.01 #訓練步長
print_flag = True #列印cost標識
lambd = 0 #L2正則化係數,為0時不進行正則化
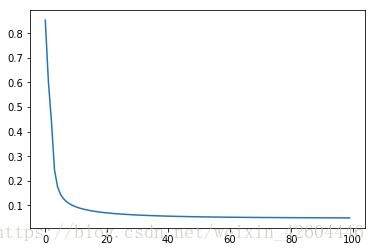
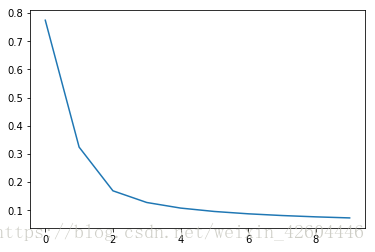
batch_size = 512 #mini_batch_size,為1時即為隨機梯度下降,為X.shape[1]時即不分批步長減至0.01,訓練次數減至100,即可得到合適的網路,效果如下(每10次全樣本訓練記錄一次cost)。
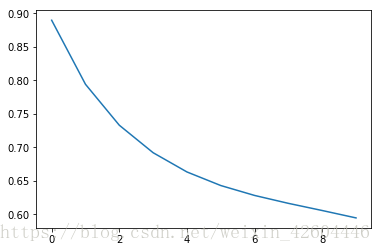
同樣的引數,使用動量梯度下降時100次全樣本訓練後並未收斂,效果如下(每10次全樣本訓練記錄一次cost,注意左下圖縱軸範圍0.6~0.9)。
可見同樣的引數時,adam的收斂速度快很多!
總結
從上面的分析和試驗,可知上述措施能夠有效的優化神經網路,令神經網路訓練時可以更快收斂。
附
相關程式碼可以在我的資源中下載!希望能幫到大家!