時間序列分析及應用 R語言 讀書筆記 02
阿新 • • 發佈:2019-01-04
第二章 基本概念
自協方差函式γt,s
自相關函式
當
隨機遊動 random walk
假設
假設時間序列Yt為下式:
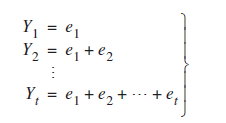
則
可以看到這裡方差是隨時間逐漸加大的
其自協方差和自相關係數為(t<=s):
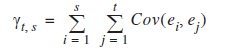
由於e是獨立同分布的所以
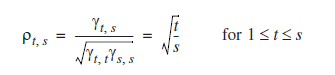
滑動平均
再次利用上面的{e}來構造一個例子
這就是滑動平均了
他的自協方差和自相關係數有以下性質:

書裡有詳細的證明,這裡不再贅述。
這裡可以看出,
平穩性
平穩性是一個重要的概念,它的基本思想是:
序列的特性,不再隨著時間的變化而變化。
表現為時間間隔前後的
對於多元函式則是時間間隔k前後的聯合分佈相同。
為簡便起見以後可能會有以下符號:
對於平穩的條件,書中給出了一個數學上更弱一點的平穩的條件:
1. 均值在所有時間上恆為常數
2.
以後指的平穩若沒有特殊說明,都是這個弱平穩。
書中可以證明:對於上面的序列{e}是一個平穩的序列(也叫白噪聲),滑動平均也是一個平穩的序列,但是隨機漫步不是一個平穩序列。
但是如果將隨即漫步差分: