一、BFS演算法思路

本演算法以無向圖為例，儲存方式採用鄰接矩陣

寬度優先遍歷需要藉助佇列，思想與二叉樹的層序遍歷類似

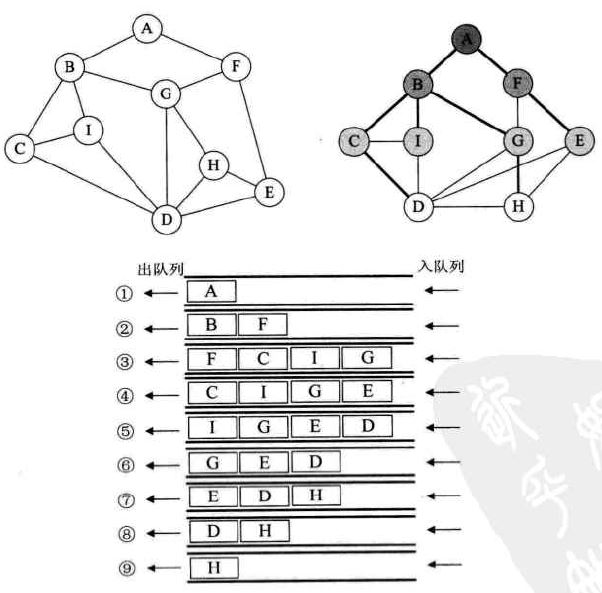
二、BFS測試用例

本演算法的測試用例為《大話資料結構》p242中的圖7-5-3

三、C程式碼鄰接矩陣的BFS實現

/*******************************************************************************************
【BFS】
Author:tmw
date:2018-2-20
********************************************************************************************/
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>


#define MAX_VERTEX 100
#define inf 65535  //表示兩點之間沒有邊相連

int visit[MAX_VERTEX];   //標記頂點是否被訪問

/**圖的鄰接矩陣的建立**/
//鄰接矩陣資料結構定義
typedef struct Martrix_Graph
{
    char vertex[MAX_VERTEX]; //儲存頂點資訊
    int edge[MAX_VERTEX][MAX_VERTEX]; //儲存邊資訊
    int vertex_number,edge_number;//儲存頂點數和邊數
}Martrix_Graph;

void Create_non_direction_martrix_Graph( Martrix_Graph *G )
{
    int i,j,k,m;
    printf("請輸入構造的無向圖的頂點數和邊數：\n");
    scanf("%d %d",&G->vertex_number,&G->edge_number);

    printf("請輸入無向圖頂點資訊（如ABCDEF....）：\n");
    char ch;
    while( ( ch = getchar() != '\n' ) );  //過濾掉前面的\n，防止\n被scanf進去
    for(i=0;i<G->vertex_number;i++)
        scanf("%c",&G->vertex[i]);

    //不相連的頂點之間的權值設為inf，包括頂點自身
    //初始化鄰接矩陣
    for(i=0;i<G->vertex_number;i++)
        for(j=0;j<G->vertex_number;j++)
            G->edge[i][j] = inf;

    //更新無向圖邊資訊
    printf("請輸入無向圖鄰接矩陣相連的邊資訊，相連標記為1\n");
    for(k=0;k<G->edge_number;k++)
    {
        scanf("%d %d %d",&i,&j,&m);
        G->edge[i][j] = m;
        G->edge[j][i] = G->edge[i][j];//無向圖是對稱陣
    }


    //列印鄰接矩陣儲存資訊，檢查正確性
    printf("---------------------構造出來的無向圖鄰接矩陣如下---------------------\n");
    for(i=0;i<G->vertex_number;i++)
    {
        for(j=0;j<G->vertex_number;j++)
            printf("%d\t",G->edge[i][j]);
        printf("\n");
    }
}
/**BFS會用到佇列這個資料結構**/
/**迴圈佇列**/
typedef struct
{
    char data[MAX_VERTEX];
    int front;  //頭指標
    int rear;   //尾指標，佇列非空則指向隊尾最後一個元素後一個位置
}SqQueue;

//佇列初始化
void InitQueue(SqQueue *Q)
{
    Q->front = 0;
    Q->rear = 0;
}
//入隊
bool EnQueue(SqQueue *Q, char e)
{
    //判斷佇列是否滿
    if( ( Q->rear+1 ) % MAX_VERTEX == Q->front )
        return false;
    Q->data[Q->rear]=e;
    Q->rear = (Q->rear+1)%MAX_VERTEX;
    return true;
}
//出隊---刪除隊首元素，並賦給e
char* DeQueue(SqQueue *Q, char *e)
{
    //判斷佇列是否為空
    if( Q->front == Q->rear )
        return NULL;
    *e = Q->data[Q->front];
    Q->front = (Q->front+1)%MAX_VERTEX;
    return e;
}
//佇列判空
bool isEmptyQueue(SqQueue *Q)
{
    return Q->front == Q->rear?true:false;
}

//無向圖鄰接矩陣BFS
void BFS_Travel(Martrix_Graph G)
{
//    int layerNumer = 0;
    SqQueue Q;
    int i,j,mark;
    char data;
    //初始化visit陣列
    for(i=0;i<G.vertex_number;i++)
        visit[i] = false;
    //初始化佇列
    InitQueue(&Q);

    //開始遍歷整個圖的頂點--預設從第一個頂點開始
    printf("此鄰接矩陣無向圖BFS的結果為：\n");
    for(i=0;i<G.vertex_number;i++)
    {
        //對未訪問的頂點做BFS
        if(!visit[i])
        {
            visit[i] = true;

            //將此頂點入隊
            EnQueue(&Q,G.vertex[i]);
//            layerNumer++;

            while(!isEmptyQueue(&Q))
            {
                DeQueue(&Q,&data);  //隊首頂點出隊，並賦值給data
                printf("%c ",data);

                //找所刪除頂點的下標，更新該下標值，以便正確找到與出隊元素相連的其他頂點
                for( j = 0;j<G.vertex_number;j++)
                    if(G.vertex[j] == data )
                        mark = j ;
                //找尋與此頂點相連且未被訪問的頂點，逐次標記、列印，併入隊
                for(j=0;j<G.vertex_number;j++)
                {
                    if(G.edge[mark][j]==1 && !visit[j])
                    {

                        visit[j] = true;
//                        printf("%c ",G.vertex[j]);
                        EnQueue(&Q,G.vertex[j]);
                    }
                }
            }
        }

    }

}
 

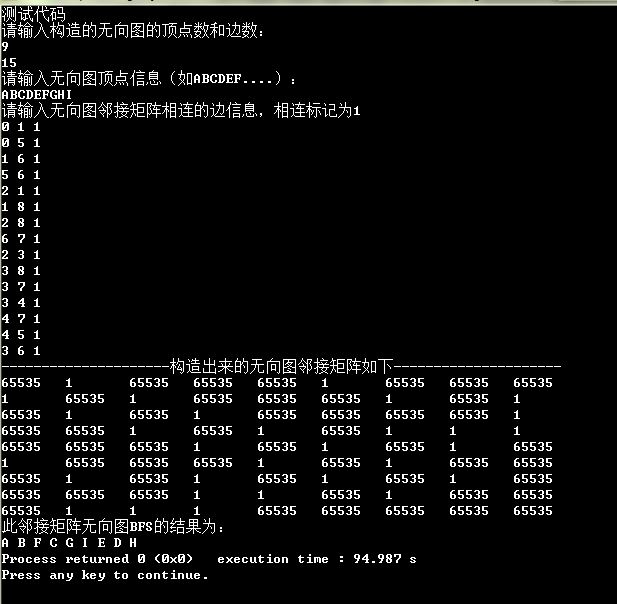
四、測試程式碼及執行結果

int main()
{
    printf("測試程式碼\n");
    Martrix_Graph G;
    Create_non_direction_martrix_Graph(&G);
    BFS_Travel(G);
    return 0;
}