樸素貝葉斯演算法及Python的簡單實現
貝葉斯演算法起源於古典數學理論,是一種分類演算法的總稱。它以貝葉斯定理為基礎,假設某待分類的樣本滿足某種概率分佈,並且可以根據已觀察到的樣本資料對該樣本進行概率計算,以得出最優的分類決策。通過計算已觀察到的樣本資料估計某待分類樣本的先驗概率,利用貝葉斯公式計算出其後驗概率,即該樣本屬於某一類的概率,選擇具有最大後驗概率的類作為該樣本所屬的類。
先驗概率是根據以往經驗和分析得到的概率。可以用P(h)來表示假設h的先驗概率,用P(D)表示將要觀察的訓練資料D的先驗概率,用P(D|h)表示假設h成立的情況下觀察到資料D的概率,關心的是P(h|D),即給定訓練資料D時h成立的概率,稱之為後驗概率。
貝葉斯公式:P(h|D)=P(D|h)P(h)/P(D),從公式可以看出P(h|D)隨著P(h)和P(D|h)的增長而增長,也可以看出P(h|D)隨著P(D)的增加而減少。考慮候選假設集合H並在其中尋找給定資料D時可能性最大的假設h。這樣的具有最大可能性的假設被稱為極大後驗(MAP)假設。確定MAP假設的方法是用貝葉斯公式計算每個候選假設的後驗概率,可能會多個屬性,且屬性之間可能存在複雜的依賴關係,這就使得P(D|h)的計算十分困難,為了簡化條件概率的求解難度,提出了一種條件獨立假設,即假設訓練資料D中,各屬性之間相互獨立。在貝葉斯演算法基礎上添上條件獨立假設,我們就稱之為樸素貝葉斯演算法。
樸素貝葉斯簡介
資料集
本部落格所用的資料集,用的是鳶尾花(Iris),如有需要可通過下方地址下載
http://archive.ics.uci.edu/ml/index.php
Python程式碼的簡單實現如下:
#coding:utf-8
# 極大似然估計 樸素貝葉斯演算法
import pandas as pd
import numpy as np
class NaiveBayes(object):
def getTrainSet(self):
dataSet = pd.read_csv('Iris.csv')
dataSetNP = np.array(dataSet) #將資料由dataframe型別轉換為陣列型別
trainData = dataSetNP[:120,:dataSetNP.shape[1]-1] #訓練資料
labels = dataSetNP[:120,dataSetNP.shape[1]-1] #訓練資料所對應的所屬型別C
testData = dataSetNP[120:,:dataSetNP.shape[1]-1] #測試資料
testlabels =dataSetNP[120:,dataSetNP.shape[1]-1] #測試資料所對應的類別C
return trainData, labels, testData, testlabels
def classify(self, trainData, labels, features):
#求labels中每個label的先驗概率
labels = list(labels) #轉換為list型別
P_y = {} #存入label的概率
for label in labels:
P_y[label] = labels.count(label)/float(len(labels)) # p = count(y) / count(Y)
#求label與feature同時發生的概率
P_xy = {}
for y in P_y.keys():
y_index = [i for i, label in enumerate(labels) if label == y] # labels中出現y值的所有數值的下標索引
for j in range(len(features)): # features[0] 在trainData[:,0]中出現的值的所有下標索引
x_index = [i for i, feature in enumerate(trainData[:,j]) if feature == features[j]]
xy_count = len(set(x_index) & set(y_index)) # set(x_index)&set(y_index)列出兩個表相同的元素
pkey = str(features[j]) + '*' + str(y)
P_xy[pkey] = xy_count / float(len(labels))
#求條件概率
P = {}
for y in P_y.keys():
for x in features:
pkey = str(x) + '|' + str(y)
P[pkey] = P_xy[str(x)+'*'+str(y)] / float(P_y[y]) #P[X1/Y] = P[X1Y]/P[Y]
#求testData每條樣例所屬類別
F = {} #testData每條樣例屬於各個類別的概率
for y in P_y:
F[y] = P_y[y]
for x in features:
F[y] = F[y]*P[str(x)+'|'+str(y)] #P[y|X] = P[X|y]*P[y]/P[X],分母相等,比較分子即可,
# 所以有F=P[X/y]*P[y]=P[x1/Y]*P[x2/Y]*P[x3|y]*P[x4|y]*P[y]
features_label = max(F, key=F.get) #概率最大值對應的類別
return features_label
def test(self,trainData, labels, testData, testlabels):
correct = 0
for i in range(len(testData)):
# Outlook Temperature Humidity Wind
features = testData[i]
# 該特徵應屬於哪一類
result = nb.classify(trainData, labels, features)
print features, '屬於', result
if nb.classify(trainData, labels, testData[i]) == testlabels[i]:
correct += 1
print correct / float(len(testlabels))
if __name__ == '__main__':
nb = NaiveBayes()
# 訓練資料,測試資料
trainData, labels, testData, testlabels = nb.getTrainSet()
nb.test(trainData, labels, testData, testlabels)
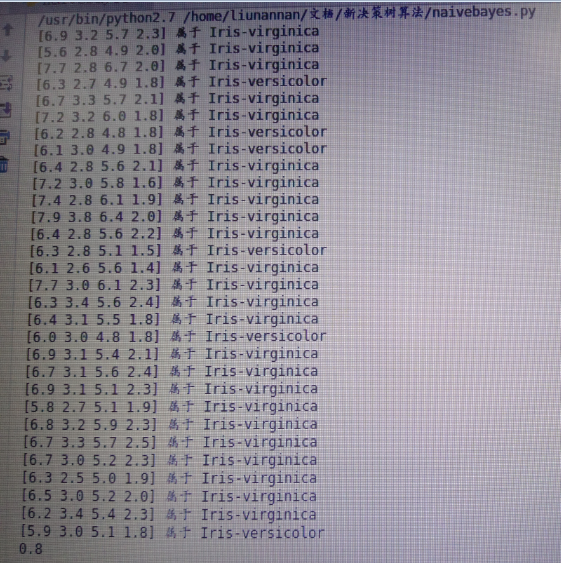
執行結果如下: