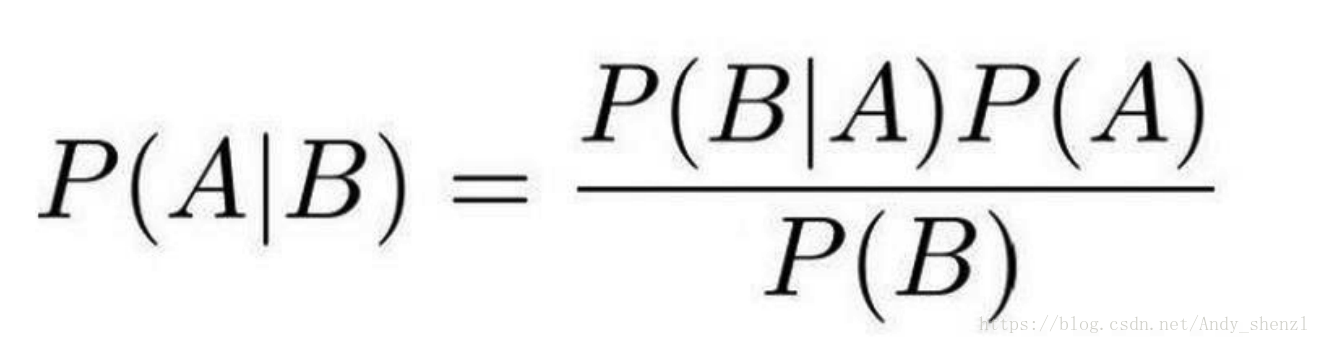貝葉斯演算法及例項python實現
目錄
貝葉斯簡介:
貝葉斯(約1701-1761) Thomas Bayes,英國數學家
貝葉斯方法源於他生前為解決一個“逆概”問題寫的一篇文章。
貝葉斯要解決的問題:
正向概率:假設袋子裡面有N個白球,M個黑球,你伸手進去摸一把, 摸出黑球的概率是多大
逆向概率:如果我們事先並不知道袋子裡面黑白球的比例,而是閉著眼睛 摸出一個(或好幾個)球,觀察這些取出來的球的顏色之後,那麼我們可 以就此對袋子裡面的黑白球的比例作出什麼樣的推測
所謂的貝葉斯定理源於他生前為解決一個“逆概”問題寫的一篇文章,而這篇文章是在他死後才由他的一位朋友發表出來的。在貝葉斯寫這篇文章之前,人們已經能夠計算“正向概率”,如“假設袋子裡面有 N 個白球,M 個黑球,你伸手進去摸一把,摸出黑球的概率是多大”。而一個自然而然的問題是反過來:“如果我們事先並不知道袋子裡面黑白球的比例,而是閉著眼睛摸出一個(或好幾個)球,觀察這些取出來的球的顏色之後,那麼我們可以就此對袋子裡面的黑白球的比例作出什麼樣的推測”。這個問題,就是所謂的逆向概率問題。
為什麼要使用貝葉斯:
1、現實世界本身就是不確定的,人類的觀察能力是有侷限性的:
--比如說我們上面說的N 個白球,M 個黑球,在現實裡面可能是無窮大的,也就是說這個數值很難具體量化
2、我們日常所觀察到的只是事物表面上的結果,因此我們需要提供一個猜測
理解貝葉斯例子:
在一個學校裡面,男生佔比60%,女生佔40%
計算過程:
1、正向概率:
假設學校裡面人的總數是 U 個(後面我們通過計算可以知道U是可以約分的),
穿長褲的(男生):U * P(Boy) * P(Pants|Boy)
P(Boy) 是男生的概率 = 60%
P(Pants|Boy) 是條件概率,即在 Boy 這個條件下穿長褲的概率是多大,這裡是 100% ,因為所有男生都穿長褲
穿長褲的(女生): U * P(Girl) * P(Pants|Girl)
穿長褲總數:U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)
穿長褲概率=穿長褲總數/校裡面人的總數=【U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)】/U
2、逆向概率計算:一個人穿了長褲,是女生的概率?
一個人穿了長褲,是女生的概率=P(Girl|Pants)=穿長褲的女生/穿長褲總數
=U * P(Girl) * P(Pants|Girl)/【U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)】--我們發現這裡U是可以消去的
=P(Girl) * P(Pants|Girl)/【P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)】
分母其實就是 P(Pants) 分子其實就是 P(Pants, Girl)
貝葉斯公式:
其中P(A|B)是在 B 發生的情況下 A 發生的可能性。
P(A)是 A 的先驗概率,之所以稱為“先驗”是因為它不考慮任何 B 方面的因素。 P(A|B)是已知 B 發生後 A 的條件概率,也由於得自 B 的取值而被稱作 A 的後驗概率。 P(B|A)是已知 A 發生後 B 的條件概率,也由於得自 A 的取值而被稱作 B 的後驗概率。 P(B)是 B 的先驗概率,也作標淮化常量(normalizing constant)。
按這些術語,貝葉斯定理可表述為:
後驗概率 = (相似度 * 先驗概率)/標淮化常量
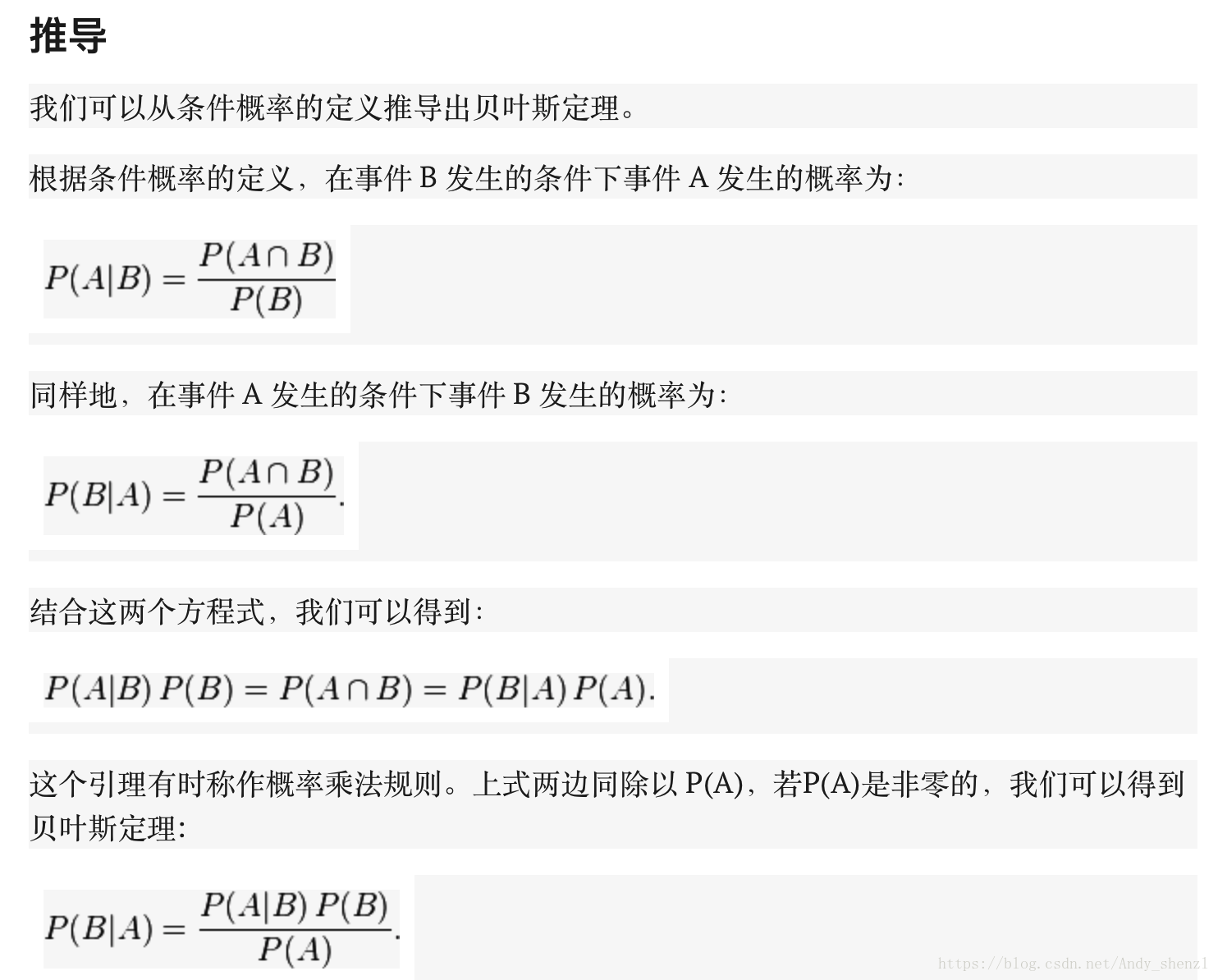
貝葉斯公式推導
通常,事件 A 在事件 B 發生的條件下的概率,與事件 B 在事件 A 發生的條件下的概率是不一樣的;然而,這兩者是有確定關係的,貝葉斯定理就是這種關係的陳述。
貝葉斯公式的用途在於通過己知三個概率來推測第四個概率。它的內容是:在 B 出現的前提下,A 出現的概率等於 A 出現的前提下 B 出現的概率乘以 A 出現的概率再除以 B 出現的概率。通過聯絡 A 與 B,計算從一個事件發生的情況下另一事件發生的概率,即從結果上溯到源頭(也即逆向概率)。
通俗地講就是當你不能確定某一個事件發生的概率時,你可以依靠與該事件本質屬性相關的事件發生的概率去推測該事件發生的概率。用數學語言表達就是:支援某項屬性的事件發生得愈多,則該事件發生的的可能性就愈大。這個推理過程有時候也叫貝葉斯推理。
python經典取球例項:
假設有兩個各裝了100個球的箱子,甲箱子中有70個紅球,30個綠球,乙箱子中有30個紅球,70個綠球。假設隨機選擇其中一個箱子,從中拿出一個球記下球色再放回原箱子,如此重複12次,記錄得到8次紅球,4次綠球。問題來了,你認為被選擇的箱子是甲箱子的概率有多大?
剛開始選擇甲乙兩箱子的先驗概率都是50%,因為是隨機二選一(這是貝葉斯定理二選一的特殊形式)。即有:
P(甲) = 0.5, P(乙) = 1 - P(甲);
這時在拿出一個球是紅球的情況下,我們就應該根據這個資訊來更新選擇的是甲箱子的先驗概率:
P(甲|紅球1) = P(紅球|甲) × P(甲) / (P(紅球|甲) × P(甲) + (P(紅球|乙) × P(乙)))
P(紅球|甲):甲箱子中拿到紅球的概率
P(紅球|乙):乙箱子中拿到紅球的概率
因此在出現一個紅球的情況下,選擇的是甲箱子的先驗概率就可被修正為:
P(甲|紅球1) = 0.7 × 0.5 / (0.7 × 0.5 + 0.3 × 0.5) = 0.7
即在出現一個紅球之後,甲乙箱子被選中的先驗概率就被修正為:
P(甲) = 0.7, P(乙) = 1 - P(甲) = 0.3;
如此重複,直到經歷8次紅球修正(概率增加),4此綠球修正(概率減少)之後,選擇的是甲箱子的概率為:96.7%。
def bayesFunc(pIsBox1, pBox1, pBox2):
return (pIsBox1 * pBox1)/((pIsBox1 * pBox1) + (1 - pIsBox1) * pBox2)
def redGreenBallProblem():
pIsBox1 = 0.5
# consider 8 red ball
for i in range(1, 9):
pIsBox1 = bayesFunc(pIsBox1, 0.7, 0.3)
print ("拿到 %d 個球是紅球是甲箱子的先驗概率: %f" % (i, pIsBox1))
# consider 4 green ball
for i in range(1, 5):
pIsBox1 = bayesFunc(pIsBox1, 0.3, 0.7)
print ("拿到 %d 個球是綠球是甲箱子的先驗概率: %f" % (i, pIsBox1))
redGreenBallProblem()
python拼寫糾正例項:
問題:我們看到使用者輸入了一個不在字典中的單詞,我們需要去猜 測:“這個傢伙到底真正想輸入的單詞是什麼呢?
比如一個人輸入了一個單詞tha,其實他真正想輸入的可能是the,也許是要輸入than等等
P(我們猜測他想輸入的單詞 | 他實際輸入的單詞)
使用者實際輸入的單詞記為D( D代表Data ,即觀測資料)
猜測1:P(h1 | D),猜測2:P(h2 | D),猜測3:P(h3 | D) 。。。
統一為:P(h | D)
P(h | D) = P(h) * P(D | h) / P(D)
使用者實際輸入的單詞記為 D ( D 代表 Data ,即觀測資料)
對於不同的具體猜測 h1 h2 h3 .. ,P(D) 都是一樣的,所以在比較 P(h1 | D) 和 P(h2 | D) 的時候我們可以忽略這個常數
P(h | D) ∝ P(h) * P(D | h) 對於給定觀測資料,一個猜測是好是壞,取決於“這個猜測本身獨 立的可能性大小(先驗概率,Prior )”和“這個猜測生成我們觀測 到的資料的可能性大小。
貝葉斯方法計算: P(h) * P(D | h),P(h) 是特定猜測的先驗概率
比如使用者輸入tlp ,那到底是 top 還是 tip ?這個時候,當最大似然 不能作出決定性的判斷時,先驗概率就可以插手進來給出指示—— “既然你無法決定,那麼我告訴你,一般來說 top 出現的程度要高許多,所以更可能他想打的是 top ”
模型比較理論
最大似然:最符合觀測資料的(即 P(D | h) 最大的)最有優勢
擲一個硬幣,觀察到的是“正”,根據最大似然估計的精神,我們應該 猜測這枚硬幣擲出“正”的概率是 1,因為這個才是能最大化 P(D | h) 的那個猜測
奧卡姆剃刀: P(h) 較大的模型有較大的優勢
奧卡姆剃刀定律(Occam's Razor, Ockham's Razor)又稱“奧康的剃刀”,它是由14世紀邏輯學家、聖方濟各會修士奧卡姆的威廉(William of Occam,約1285年至1349年)提出。這個原理稱為“如無必要,勿增實體”,即“簡單有效原理”。正如他在《箴言書注》2卷15題說“切勿浪費較多東西去做,用較少的東西,同樣可以做好的事情。”(百度百科)
原理具體內容為:1.避重趨輕 2.避繁逐簡 3.以簡御繁 4.避虛就實
剃刀原則從來沒有說簡單的理論就是正確的理論,通常表述為“當兩個假說具有完全相同的解釋力和預測力時,我們以那個較為簡單的假說作為討論依據。”(科學松鼠會)
剃刀原則不是一個理論而是一個原理,它的目的是為了精簡抽象實體。它不能被證明也不能被證偽,因為它是一個規範性的思考原則。大部分情況下,應用奧卡姆剃刀原理是合適的;但是這不代表奧卡姆剃刀就是正確的。(知乎)
總結一下,剃刀原則並不是一種定理(在數學上有推導,數學之美——劉未鵬),而是一種思維方式,可用於指導我們的工作,比如我們可以用A和B達到同樣的效果,但B更簡單,於是我們選擇B。同時,也有人說可能因為能力不足,於是我們選擇更簡單的方式來處理問題,這也是剃刀的原則的一種應用吧。舉個貼切的例子,做決策樹分析的時候,採用9個屬性的預測效能和5個屬性的預測效能是相似的,那麼我們就會選擇5個屬性來預測。
如果平面上有 N 個點,近似構成一條直線,但絕不精確地位於一條直線 上。這時我們既可以用直線來擬合(模型1),也可以用二階多項式(模 型2)擬合,也可以用三階多項式(模型3),特別地,用 N-1 階多項式 便能夠保證肯定能完美通過 N 個數據點。那麼,這些可能的模型之中到 底哪個是最靠譜的呢?
奧卡姆剃刀:越是高階的多項式越是不常見
求解:argmaxc P(c|w) -> argmaxc P(w|c) P(c) / P(w)
- P(c), 文章中出現一個正確拼寫詞 c 的概率, 也就是說, 在英語文章中, c 出現的概率有多大
- P(w|c), 在使用者想鍵入 c 的情況下敲成 w 的概率. 因為這個是代表使用者會以多大的概率把 c 敲錯成 w
- argmaxc, 用來列舉所有可能的 c 並且選取概率最大的
import re, collections
def words(text): return re.findall('[a-z]+', text.lower()) #把語料中的單詞全部抽取出來, 轉成小寫, 並且去除單詞中間的特殊符號
def train(features):
model = collections.defaultdict(lambda: 1)
for f in features:
model[f] += 1
return model
#要是遇到我們從來沒有過見過的新詞怎麼辦. 假如說一個詞拼寫完全正確, 但是語料庫中沒有包含這個詞, 從而這個詞也永遠不會出現在訓練集中. 於是, 我們就要返回出現這個詞的概率是0. 這個情況不太妙, 因為概率為0這個代表了這個事件絕對不可能發生, 而在我們的概率模型中, 我們期望用一個很小的概率來代表這種情況. lambda: 1
NWORDS = train(words(open('big.txt').read()))#big.txt為語料庫
alphabet = 'abcdefghijklmnopqrstuvwxyz'
#編輯距離:
#兩個詞之間的編輯距離定義為使用了幾次插入(在詞中插入一個單字母), 刪除(刪除一個單字母), 交換(交換相鄰兩個字母), 替換(把一個字母換成另一個)的操作從一個詞變到另一個詞.
def edits1(word):#改變其中一個字母
n = len(word)
return set([word[0:i]+word[i+1:] for i in range(n)] + # 刪除某個字母
[word[0:i]+word[i+1]+word[i]+word[i+2:] for i in range(n-1)] + # 改變其中兩個字母前後順序
[word[0:i]+c+word[i+1:] for i in range(n) for c in alphabet] + # 替換某個字母
[word[0:i]+c+word[i:] for i in range(n+1) for c in alphabet]) # 插入某個字母
def known_edits2(word):#改變兩個字母
return set(e2 for e1 in edits1(word) for e2 in edits1(e1) if e2 in NWORDS)
def known(words): return set(w for w in words if w in NWORDS)
#如果known(set)非空, candidate 就會選取這個集合, 而不繼續計算後面的
def correct(word):
candidates = known([word]) or known(edits1(word)) or known_edits2(word) or [word]
return max(candidates, key=lambda w: NWORDS[w])比如我們輸入了morw,那麼根據語料庫的統計,我們應該輸入的是more