編寫：土豆 MoreZheng SlyneD
校對：碧海聽滔 Molly
總校對與稽核：寒小陽

本系列由斯坦福大學CS231n課後作業提供
CS231N - Assignment2 - Q4 - ConvNet on CIFAR-10

問題描述：使用IPython Notebook（現版本為jupyter notebook，如果安裝anaconda完整版會內建），在ConvolutionalNetworks.ipynb檔案中，你將實現幾個卷積神經網路中常用的新層。使用CIFAR-10資料，訓練出一個深度較淺的卷積神經網路，最後盡你所能訓練出一個最佳的神經網路。

任務

實現卷積神經網路卷積層

的前向計算與反向傳導
實現卷積神經網路池化層的前向計算與反向傳導
卷積層與池化層的加速

卷積神經網路結構

常規神經網路的輸入是一個向量，經一系列隱層的轉換後，全連線輸出。在分類問題中，它輸出的值被看做是不同類別的評分值。

神經網路的輸入可不可以是圖片呢？

常規神經網路對於大尺寸影象效果不盡人意。圖片的畫素點過多，處理起來極為複雜。因此在處理圖片的過程中較為合理地降維成為了一個研究方向。於是，在基本神經網路的結構上，衍生出了一種新的神經網路結構，我們稱之為卷積神經網路。

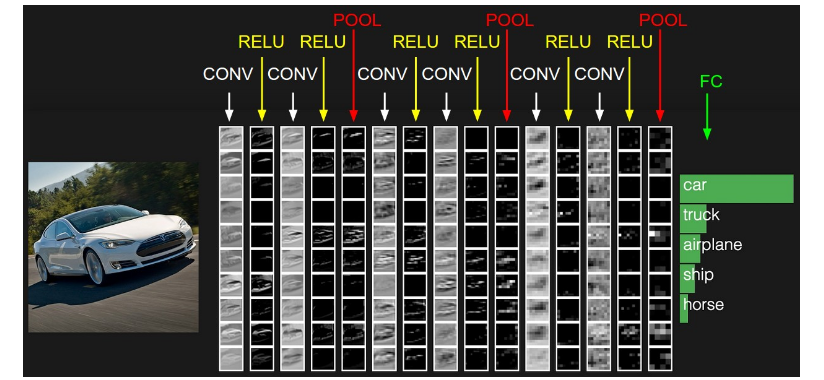
下圖是一個傳統多層卷積神經網路結構：

可以看出，上圖網路結構開始為“卷積層（CONV），relu層（RELU），池化層（POOL）”C-R-P週期迴圈，最後由全連線層（FC）輸出結果。

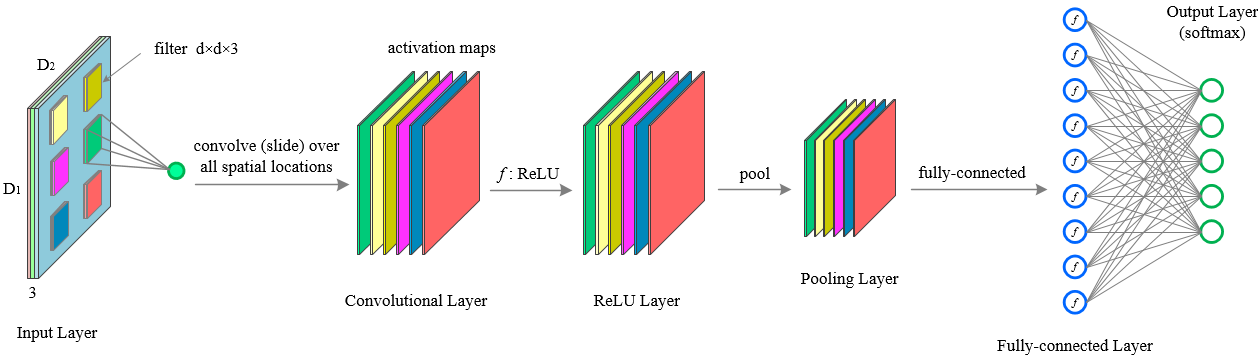
注：實際應用的過程中常常不限於C-R-P迴圈，也有可能是C-C-R-P等等

設啟用函式為fsigmoid(−)$f_{sigmoid}(-)$，池化操作為pool(−)$pool(-)$，x代表輸入的影象畫素矩陣，w代表過濾層（卷積核），b代表偏置。C-R-P週期則有下面的計算公式：

xlj=pool(frelu(∑i∈Mjxl−1i∗wlij+blj))$$x_j^l=pool(f_{relu}(\sum _{i\in M_j}{x}_i^{l-1}\ast w_{ij}^l+b_j^l))$$
卷積神經網路的理解比較困難，為了更好地理解，我們先講解過程再討論實際應用。

卷積層的樸素（無加速演算法）實現與理解

（在實際應用過程中，一般使用加速處理的卷積層，這裡表現的是原始版本）

卷積層元素

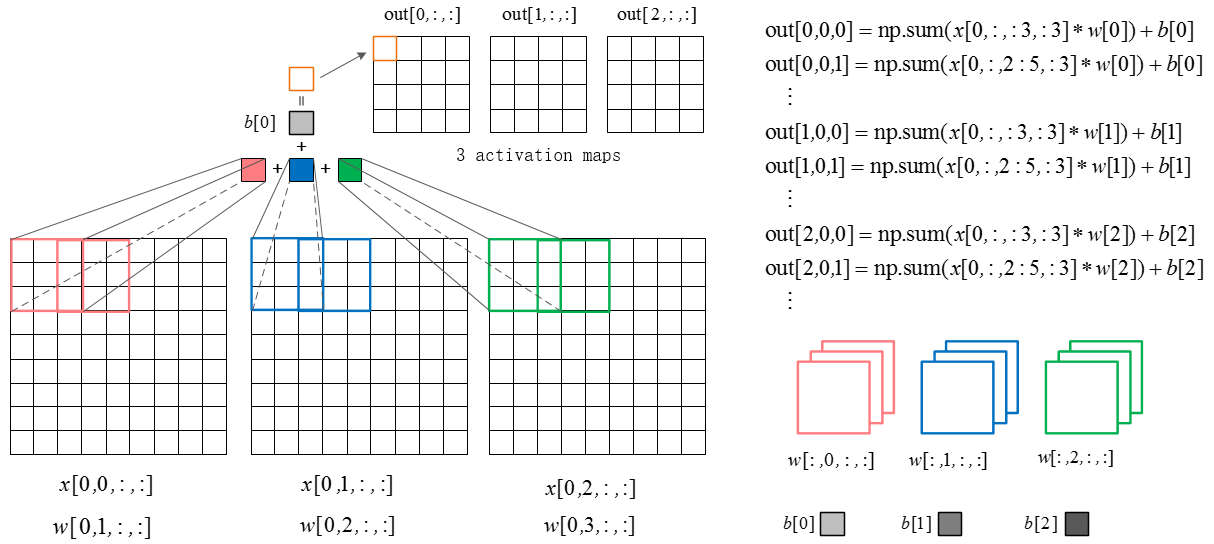
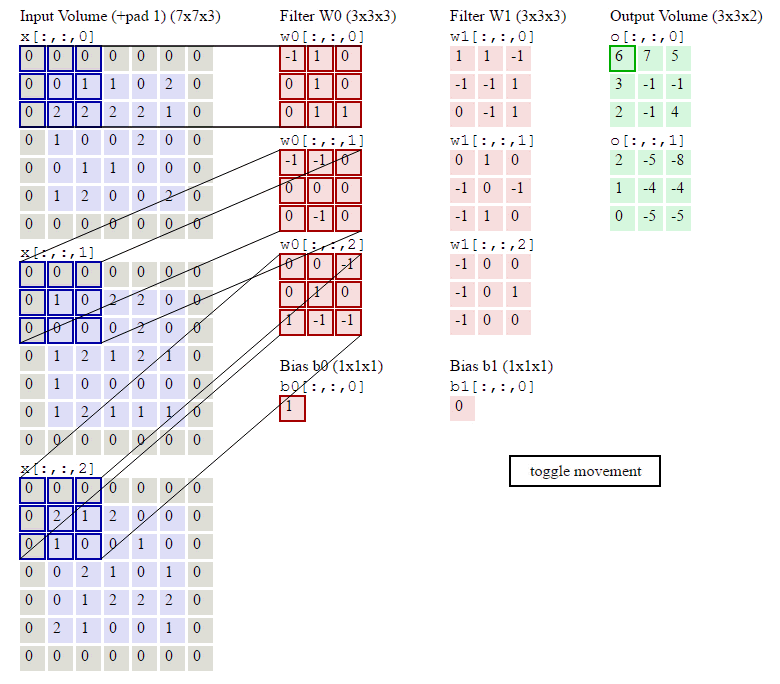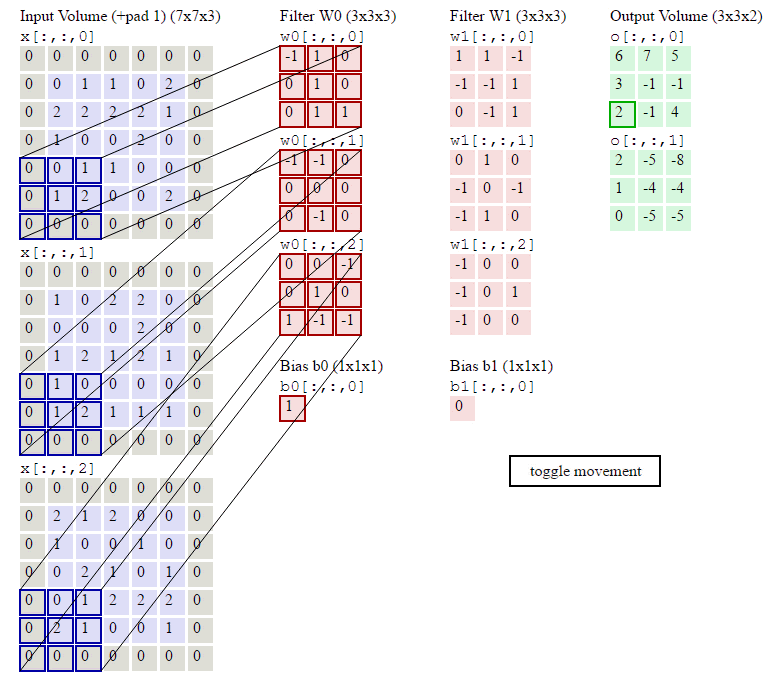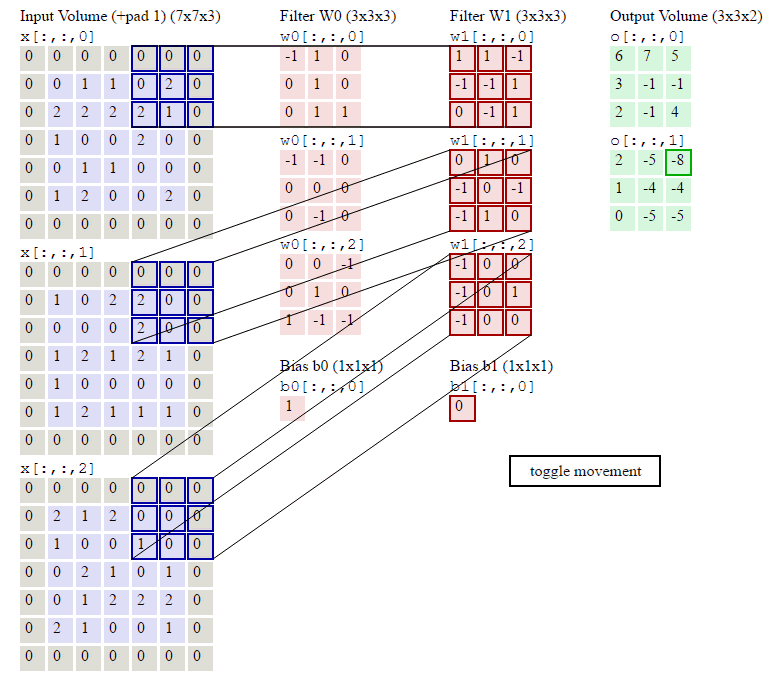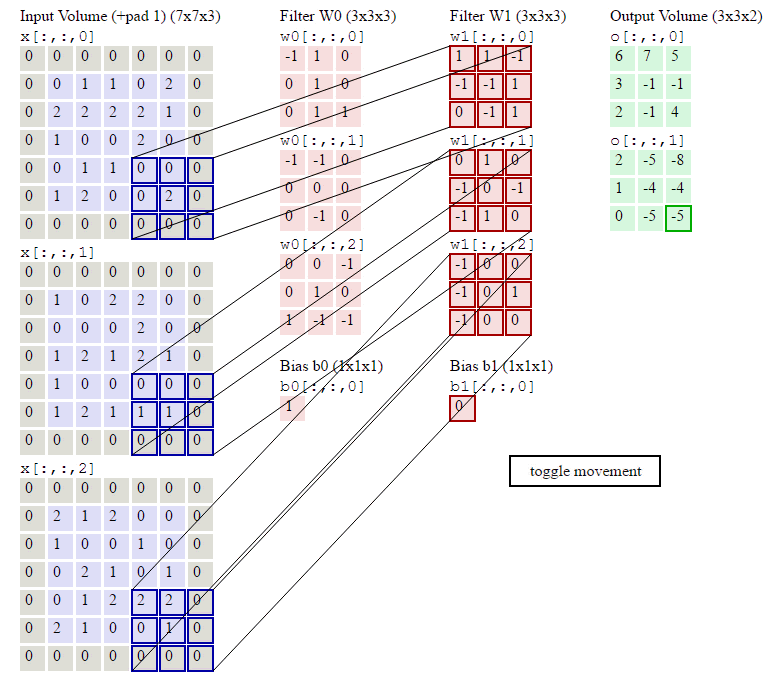
下圖是卷積層的元素：輸入圖片與過濾引數。

輸入圖片（image）：輸入層（Input Layer）有3個深度（D1，D2，D3，通常代表圖片的三個通道RGB）。我可以將每個深度獨立出來，看成三幅圖片。圖片的大小為32*32。

過濾引數（filter）：過濾器有很多稱呼，如“卷積核”、“過濾層”或者“特徵檢測器”。不要被名詞坑了。過濾器也有3個深度（D1，D2，D3），就是與輸入圖片的深度進行一一對應，方便乘積操作。過濾器視窗一般比輸入圖片視窗小。

卷積層的前向計算

下圖是卷積層的具體實現方法。

x代表圖片image矩陣，w代表過濾層矩陣。各個過濾器分別與image的一部分進行點積，用點積結果排列成結果，這就是卷積過程。下面的動圖就是卷積過程。

上圖中我們看到每次視窗移動2格。這2格就是每次卷積的移動步長。

我們看到原來的圖片在周圍填充了一圈0。填充0的寬度即為每次卷積的填充寬度padding（上圖的填充寬度就是1）

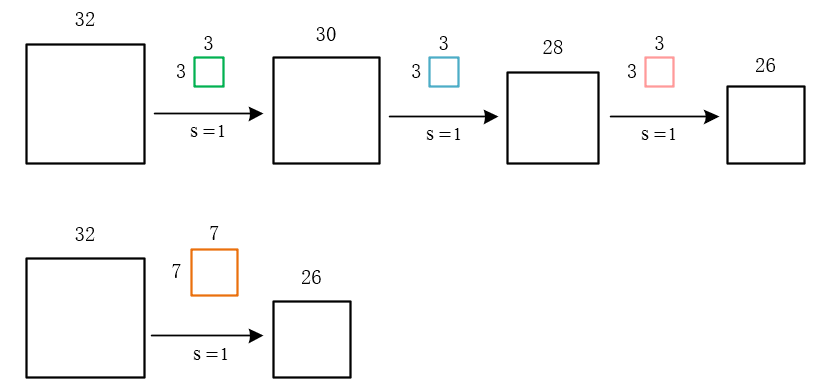
移動步長很好理解，但為什麼要填充呢？假設我們不填充。如下圖：

會發現每次卷積之後都會有維度降低。淺層卷積網路可能沒有什麼問題。但是深層卷積可能在網路沒到最後的時候維度即降為0。
這顯然不是我們所希望的。

當然，如果有意願用卷積計算去降維也可以，不過我們更喜歡用池化層的池化操作降維。為甚？因為卷基層和池化層各有分工！我們先來了解卷積層的作用。

卷積層正向卷積過程程式碼實現

def conv_forward_naive(x, w, b, conv_param):
    """
    A naive implementation of the forward pass for a convolutional layer.

    The input consists of N data points, each with C channels, height H and
    width W. We convolve each input with F different filters, where each filter
    spans all C channels and has height HH and width HH.

    Input:
    - x: Input data of shape (N, C, H, W)
    - w: Filter weights of shape (F, C, HH, WW)
    - b: Biases, of shape (F,)
    - conv_param: A dictionary with the following keys:
      - 'stride': The number of pixels between adjacent receptive fields in the
        horizontal and vertical directions.
      - 'pad': The number of pixels that will be used to zero-pad the input.

    Returns a tuple of:
    - out: Output data, of shape (N, F, H', W') where H' and W' are given by
      H' = 1 + (H + 2 * pad - HH) / stride
      W' = 1 + (W + 2 * pad - WW) / stride
    - cache: (x, w, b, conv_param)
    """
    ##########################################################################################
    # TODO: Implement the convolutional forward pass.    任務:完成帶卷積操作的前向傳播          #
    # Hint: you can use the function np.pad for padding. 提示:可以使用np.pad函式實現padding操作 #
    ##########################################################################################
    N, C, H, W = x.shape        # N個樣本，C個通道，H的高度，W的寬度
    F, C, HH, WW = w.shape      # F個過濾器，C個通道，HH的過濾器高度，WW的過濾器寬度
    stride = conv_param['stride']   # 過濾器每次移動的步長
    pad = conv_param['pad']         # 圖片填充的寬度

    ## 計算卷積結果矩陣的大小並分配全零值佔位
    new_H = 1 + int((H + 2 * pad - HH) / stride)
    new_W = 1 + int((W + 2 * pad - WW) / stride)
    out = np.zeros([N, F, new_H, new_W])

    ## 卷積開始
    for n in range(N):
        for f in range(F):
            ## 臨時分配(new_H, new_W)大小的全偏移項卷積矩陣，（即提前加上偏移項b[f]）
            conv_newH_newW = np.ones([new_H, new_W])*b[f]
            for c in range(C):
                ## 填充原始矩陣，填充大小為pad，填充值為0
                pedded_x = np.lib.pad(x[n, c], pad_width=pad, mode='constant', constant_values=0)
                for i in range(new_H):
                    for j in range(new_W):
                        conv_newH_newW[i, j] +=  np.sum(pedded_x[i * stride: i * stride+HH, j * stride: j * stride + WW] * w[f, c, :, :] )
                out[n,f] = conv_newH_newW
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b, conv_param)
    return out, cache

卷積層的個人理解

對卷積層的作用，很多人的說法莫衷一是。我這裡談談自己的理解(未必精準)。

1. 實現某畫素點多通道以及周圍資訊的整合

說白了就是將一個畫素與其周圍的點建立聯絡。我們用將一點及其周邊“卷”起來求和計算。那麼每一層卷積必然是將一個畫素點與周圍建立聯絡的過程。

這麼說起來“Convolution”翻譯為“卷和”更恰當，其實卷積的“積”就是積分的意思

2. 我們先講一個喪心病狂的故事

如果你每天總偷看別的美女不注意女朋友，那麼女朋友每天都要扇你一巴掌。打你一巴掌後，臉的一部分就腫了。你的臉就是圖片，女朋友的巴掌就是卷積核層。每打一巴掌，相當於“卷積核”作用臉部一個地方“做卷積”。臉腫了相當於臉部“卷積後”輸出的結果。
如果有一天，女友忍無可忍，連續扇你嘴巴，那麼問題就出現了：上一次扇你鼓起來的包還沒消腫，第二個巴掌就來了，這就是多層“卷積”。

女友再狠一點，頻率越來越高，以至於你都辨別不清時間間隔了。那麼，求和就變成積分了。使用“積分運算的卷積”就是我們在大學數學《概率論與數理統計》中學到的“卷積運算”。

女友打你在不同的位置，自然會有不同的身體反應。根據打你後卷積後身體的反應卷積結果可以判斷出打到什麼位置了。

身體反應(卷積結果)	可能推論
腫了	打到臉了
紅了	打到肚子了
沒反應	打到骨頭了
女友手疼	打到骨刺了
更愛她了	變態
沒有感覺	單身狗的幻想

這麼一解釋卷積層的解釋果然很明顯。。。。嗯，對。。。。我自己都信了。。。。

3. 影象處理中模板的概念

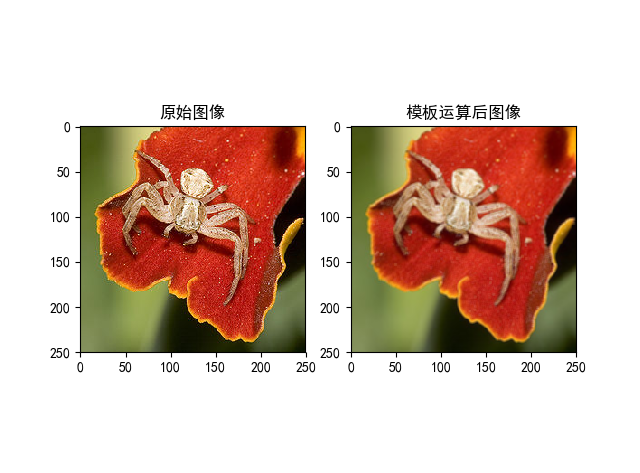
圖片卷積不是一個新概念，在傳統影象處理中就有與“卷積運算”相同的“模板運算”。模板即一個矩陣方塊，在這裡你可以認為是卷積核，模板運算方法與卷積運算方法相同。如下面的一個模板

19∗⎡⎣⎢111111111⎤⎦⎥$$\frac{1}{9}\ast \left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$
圖片用這個模板進行運算後，可以得到類似於如下的效果。

上面的那種模板就是“低通濾波模板”的一種。
通過改變方陣的數值與大小，可以生成很多新的模板。如“高通濾波模板”，“邊緣檢測模板”，“匹配濾波邊緣檢測模板”等等。。不同的模板運用在不同的場景中。

那麼又問題來了：我們該在什麼時候，用什麼數值的模板？

答案比價複雜。傳統的模板選擇，憑藉的是演算法工程師們的經驗。但現在，我們不怕了!~~神經網路幫我們訓練模板的引數。在多層神經網路中，圖片可以新增很多個模板（即卷積層），一個或多個模板（卷積層）負責一項工作。圖片在卷積神經網路的一次前向過程，就相當於對影象做一次特定的處理。

卷積層反向求導

前面我們介紹了卷積層的前向計算。大致瞭解了卷積的作用，但是神經網路的引數是怎麼來的呢？引數的獲取是一個迭代的訓練的過程，每次反向傳播都糾正引數，減小誤差。（具體細節請看Q1~Q3中關於神經網路“前向計算，反向傳播”的講解。）
上文提到了C-R-P週期計算公式。

xlj=pool(frelu(∑i∈Mjxl−1i∗wlij+blj))$$x_j^l=pool(f_{relu}(\sum _{i\in M_j}{x}_i^{l-1}\ast w_{ij}^l+b_j^l))$$
frelu(−)$f_{relu}(-)$為relu啟用函式，池化操作用pool(−)$pool(-)$表示，像畫素矩陣，w代表過濾層（卷積核），b代表偏置。編寫卷積層反向傳播時，暫時不用考慮池化層，與啟用函式。我們可以用g()代指卷積層後所有的操作。所以這一層的反向對x求導可以簡化為如下操作。
⎧⎩⎨⎪⎪⎪⎪g(x∗w+b)=g(out)out=x∗w+b∂g∂x=∂g∂out∗∂out∂x$$\{\begin{array}{c}g(x\ast w+b)=g(out)\\ out=x\ast w+b\\ \frac{\mathrm{\partial }g}{\mathrm{\partial }x}=\frac{\mathrm{\partial }g}{\mathrm{\partial }out}\ast \frac{\mathrm{\partial }out}{\mathrm{\partial }x}\end{array}$$
在斯坦福CS231n課程作業中，把無實際用處的g$g$忽略。記∂x=

相關推薦

斯坦福CS231n作業程式碼（漢化）Assignment 2 Q4

編寫：土豆 MoreZheng SlyneD 校對：碧海聽滔 Molly 總校對與稽核：寒小陽 本系列由斯坦福大學CS231n課後作業提供 CS231N - Assignment2 - Q4 - ConvNet on CIFAR-10 問

斯坦福CS231n作業程式碼（漢化）Assignment 2 Q1

一段關於神經網路的故事 編寫：土豆 MoreZheng SlyneD 校對：碧海聽滔 Molly 總校對與稽核：寒小陽 To-Do： [x] 統一所有的數學符號和程式碼符號 [x] 統一所有的術語名稱 [x] 術語

斯坦福CS231n作業程式碼（漢化）Assignment 2 Q5

TensorFlow是個什麼東東？ 編寫：土豆 MoreZheng SlyneD 校對：碧海聽滔 Molly 總校對與稽核：寒小陽 在前面的作業中你已經寫了很多程式碼來實現很多的神經網路功能。Dropout, Batch Norm 和 2D卷積

斯坦福CS231n作業程式碼（漢化）Assignment 1

[CS231N - Assignment1 - Q5 - Image features exercises] 編寫：郭承坤 觀自在降魔 Fanli SlyneD 校對：毛麗 總校對與稽核：寒小陽 我們已經看到，通過用輸入影象的畫素訓練的線性分類器對影

【ZedGraph】刪除或重新命名（漢化）右鍵選單

本文結合網路資源，結合自身實踐進行了部分整理和改動，現逐步完善中，內容僅供參考。 網路資源部分轉載自：http://blog.sina.com.cn/main_v5/ria/private.html?uid=1806259402 在zedgraph生成的圖表中，右鍵選單會出

【Mac】資料夾多語言設定（漢化）

當我們使用Mac中文語言的時候，使用終端Terminal看到的資料夾列表和直接在Finder裡面看到的不一樣。經常我們使用一箇中文的資料夾在終端cd選擇的時候切換輸入法會感覺比較噁心。 但是系統預設的幾個資料夾“桌面”,“下載”等在終端看到的卻是英文的 “De

Mondrian 表頭中文顯示（漢化）

Mondrian（V3.5）前臺展示使用了JPivot，而Jpivot的表頭中文顯示有亂碼，改成可顯示中文，見下圖 在對應的XML中， <Dimension name="xxx" foreignKey="xxx" caption="&#26376;&am

ionic1使用ImagePicker外掛並且顯示中文（漢化）

在使用ionic開發時，開啟相簿應該是使用比較頻繁的外掛之一。下面講講我在專案中使用（這部分官方比較詳細，就簡單描述）以及解決外掛顯示英文問題1、imagepicker安裝cordova plugin add cordova-plugin-image-picker2、在ion

斯坦福cs231n學習筆記（8）------神經網路訓練細節（資料預處理、權重初始化）

神經網路訓練細節系列筆記： 這一篇，我們將繼續介紹神經網路訓練細節。 一、Data Preprocessing（資料預處理） 如圖是原始資料，資料矩陣X有三種常見的資料預處理形式，其中我們假定X的大小為[N×D]（N是資料的數量，D是它們的維數

為eclipse EE（漢化版） 配置Tomcat服務器

好的 -- 資源 鼠標 image 分享圖片 blog 發的 發現 　　很多小朋友在初次使用eclipse進行web開發的時候，很是蒙蔽。以前都是文本編輯器寫好，做好目錄結構，往tomcat下一扔，重啟，搞定。 如今用上eclipse了，反而不適應了。 　　這篇文章就來帶

CS231N作業記錄（持續更新中）

ssi net tail 安裝ipython ipy 工作 href https 準備 參考資料：《 cs231n 課程作業 Assignment 1 》https://blog.csdn.net/zhangxb35/article/details/55223825 一

斯坦福CS231n專案實戰（一）：k最近鄰（kNN）分類演算法

k最近鄰分類（kNN，K Nearest neighbor)分類演算法是一種最簡單的分類器之一。在kNN演算法訓練過程中，它將所有訓練樣本的輸入和輸出label都儲存起來。測試過程中，計算測試樣本與每個訓練樣本的L1或L2距離，選取與測試樣本距離最近的前k個

斯坦福cs231n學習筆記（11）------神經網路訓練細節（梯度下降演算法大總結/SGD/Momentum/AdaGrad/RMSProp/Adam/牛頓法）

神經網路訓練細節系列筆記： 通過學習，我們知道，因為訓練神經網路有個過程: <1>Sample 獲得一批資料； <2>Forward 通過計算圖前向傳播，獲得loss； <3>Backprop 反向傳播計算梯度，這

windows下配置webstorm（漢化及破解）

WebStorm是一款強大的HTML5/JavaScript Web前端開發工具，被廣大JS開發者譽為“Web前端開發神器”。WebStorm 8全新特性中包括對AngularJS的支援，能夠高效準確地

Python環境搭建（win）——Pycharm（破解+漢化）

Pycharm搭建方法（破解+漢化）： 本文以pycharm2019.2為例 寫在前面：有能力的朋友，希望大家支援正版。 IDE是整合開發環境 “Integrated Development Environment” 的縮寫。Python的IDE有很多，除了官方自帶的IDLE，網上推薦的還有Eclipse+P

集美大學網絡1413第九次作業成績（團隊五） -- 測試與發布（Alpha版本）

ima worker str ges 運行 .cn png www text NO.NE團隊的項目鏈接有效，六個核桃和六指神功團隊可以請教下他們，避免因IP地址無效或者因tomcat不打開就不能訪問的情況，畢竟助教沒辦法知道此時此刻它是開著還是關閉啊啊啊。。。 題目 團隊作

個人作業3-（Alpha階段）

命令行工具 叠代 big 價值 管理工具 導致 自動化測試 並行 中間 201421123108 王坤彬 網絡1414 一、 總結自己的alpha 過程 1.團隊的整體情況 Alpha階段我們團隊項目進行的很順利，這跟隊長合理的計劃和安排以及我們每位成員的積極配合是分不開

UVA 221 城市化地圖（離散化）

span uva 部分 精度 spa 最大的 分析 重疊 pan 題意： 分析： 記錄一個一開始就想錯的觀點， 以為只要把x 和 width放大到到足夠大（例如10000倍，倍數越高精度越高），然後排序填充一下數軸就可以，就可以解決x坐標是小數的問題。但這樣打了一下，發

團隊作業4（Alpha版本）

round images cells 路徑 第一次 pan logs 音樂 記錄 項目名稱：音樂播放器 項目成員： 張慧敏（201421122032） 蘇曉薇（201421031033）

對Java Serializable（序列化）的理解和總結

編碼 多種方法 light 定制 http 學習 功能 垃圾回收 對象序列化保存 1、序列化是幹什麽的？ 簡單說就是為了保存在內存中的各種對象的狀態（也就是實例變量，不是方法），並且可以把保存的對象狀態再讀出來。雖然你可以用你自己的各種各樣的方法來保存objec