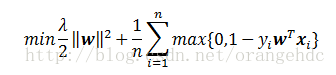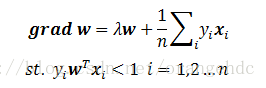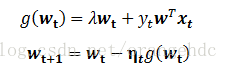隨機梯度下降法求解SVM(附matlab程式碼)
阿新 • • 發佈:2019-01-04
隨機梯度下降法(Stochastic Gradient Descent)求解以下的線性SVM模型:
w的梯度為:
傳統的梯度下降法需要把所有樣本都帶入計算,對於一個樣本數為n的d維樣本,每次迭代求一次梯度,計算複雜度為O(nd) ,當處理的資料量很大而且迭代次數比較多的時候,程式執行時間就會非常慢。
隨機梯度下降法每次迭代不再是找到一個全域性最優的下降方向,而是用梯度的無偏估計 來代替梯度。每次更新過程為:
由於隨機梯度每次迭代採用單個樣本來近似全域性最優的梯度方向,迭代的步長應適當選小一些以使得隨機梯度下降過程儘可能接近於真實的梯度下降法。
下面我用matlab寫的一個demo,速度不是很快,跑 USPS資料庫(二進位制格式)csdn下載連結(mat格式),要五分鐘,準確率88%左右,效果一般:
clear; load E:\dataset\USPS\USPS.mat; % data format: % Xtr n1*dim % Xte n2*dim % Ytr n1*1 % Yte n2*1 % warning: labels must range from 1 to n, n is the number of labels % other label values will make mistakes u=unique(Ytr); Nclass=length(u); allw=[];allb=[]; step=0.01;C=0.1; param.iterations=1; param.lambda=1e-3; param.biaScale=1; param.t0=100; tic; for classname=1:1:Nclass temp_Ytr=change_label(Ytr,classname); [w,b] = sgd_svm(Xtr,temp_Ytr, param); allw=[allw;w]; allb=[allb;b]; fprintf('class %d is done \n', classname); end [accuracy predict_label]=my_svmpredict(Xte, Yte, allw, allb); fprintf(' accuracy is %.2f percent.\n' , accuracy*100 ); toc;
function [temp_Ytr] = change_label(Ytr,classname)
temp_Ytr=Ytr;
tep2=find(Ytr~=classname);
tep1=find(Ytr==classname);
temp_Ytr(tep2)=-1;
temp_Ytr(tep1)= 1;function [true_W,b]=sgd_svm(X,Y,param) % input: % X is n*dim % Y is n*1 (label is 1 or 0) % output: % true_W is dim*1 ,so the score is X*W'+b % b is 1*1 number iterations=param.iterations;%10 lambda=param.lambda;%1e-3 biaScale=param.biaScale;%0 t0=param.t0;%100 t=t0; w=zeros(1,size(X,2)); bias=0; for k=1:1:iterations for i=1:1:size(X,1) t=t+1; alpha = (1.0/(lambda*t)); if(Y(i)*(X(i,:)*w'+bias)<1) bias=bias+alpha*Y(i)*biaScale; w=w+alpha*Y(i,1).*X(i,:); end end end b=bias; true_W=w;
function [accuracy predict_label]=my_svmpredict(Xte, Yte, allw, allb)
% allw is nclass * dim
% allb is nclass * 1
% Yte must range from 1 to nclass, other label values will make mistakes
score = Xte * allw'+repmat(allb',[size(Bte,1),1]);
[bb c]=sort(score,2,'descend');
predict_label=c(:,1);
temp = predict_label((predict_label-Yte)==0);
right=size( temp,1 );
accuracy=right/size(Yte,1);