剛學習了計算機圖形學這門課程，為奠定根基的演算法所傾倒，特此記錄一二。

Cohen－Sutherland 演算法

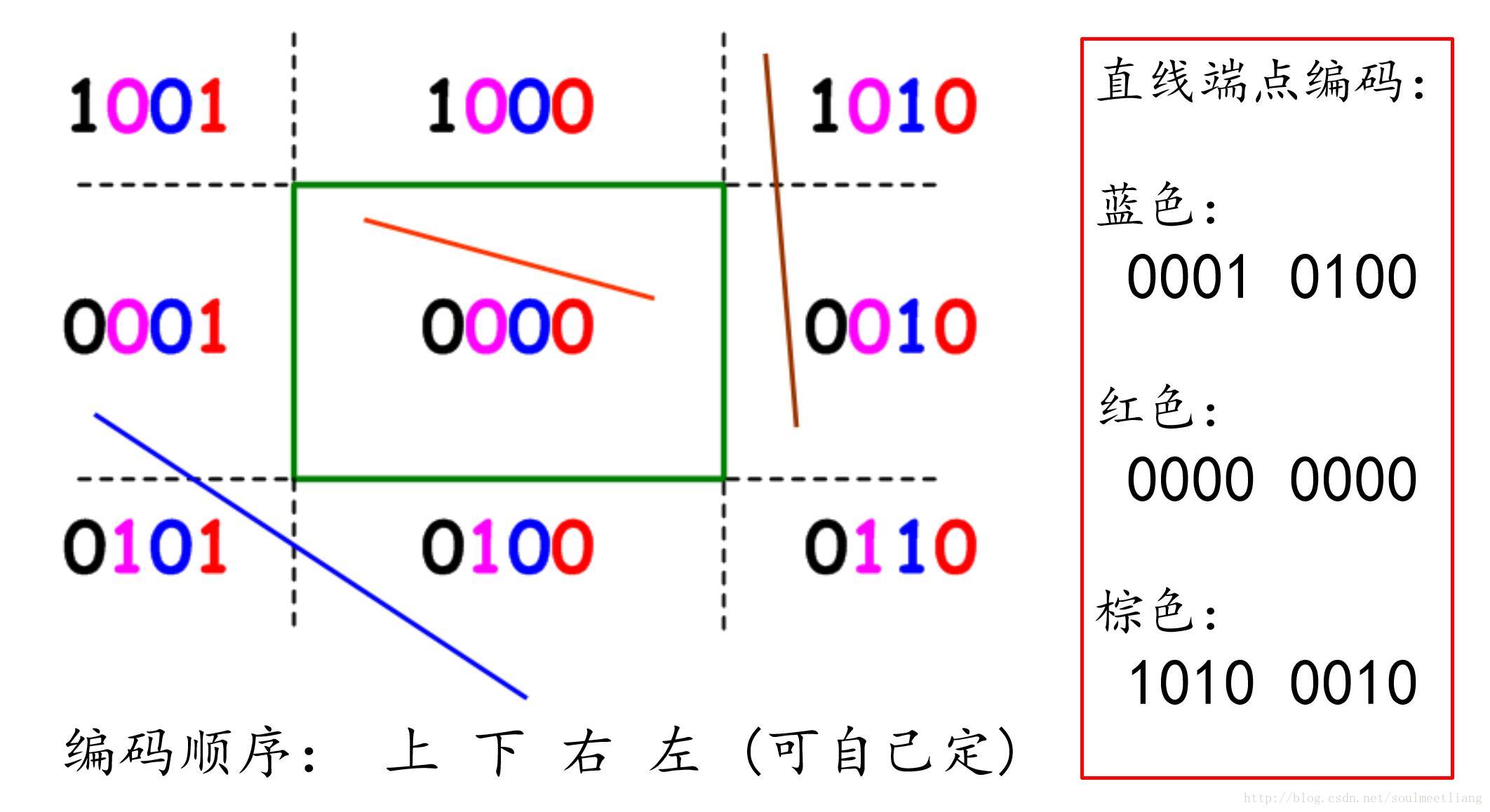
編碼

• Cohen-Sutherland 演算法是早期圖形學演算法中的一顆明珠，這種演算法使用了一種較少使用的編碼方法，較好地解決了直線段的剪裁問題，在效率和簡便性上均表現良好。
• 為介紹 Cohen-Sutherland 演算法，我們先描述對窗體所在平面的編碼。

與或

• Cohen-Sutherland 演算法的優點在於，可根據簡單的直線端點間的“與”、“或”操作，排除大量無需剪裁的直線段。對這些直線段，因無需進行與邊界間的交點計算以及相應的實、虛交點判別，所以大大提高了檢測與計算效率。
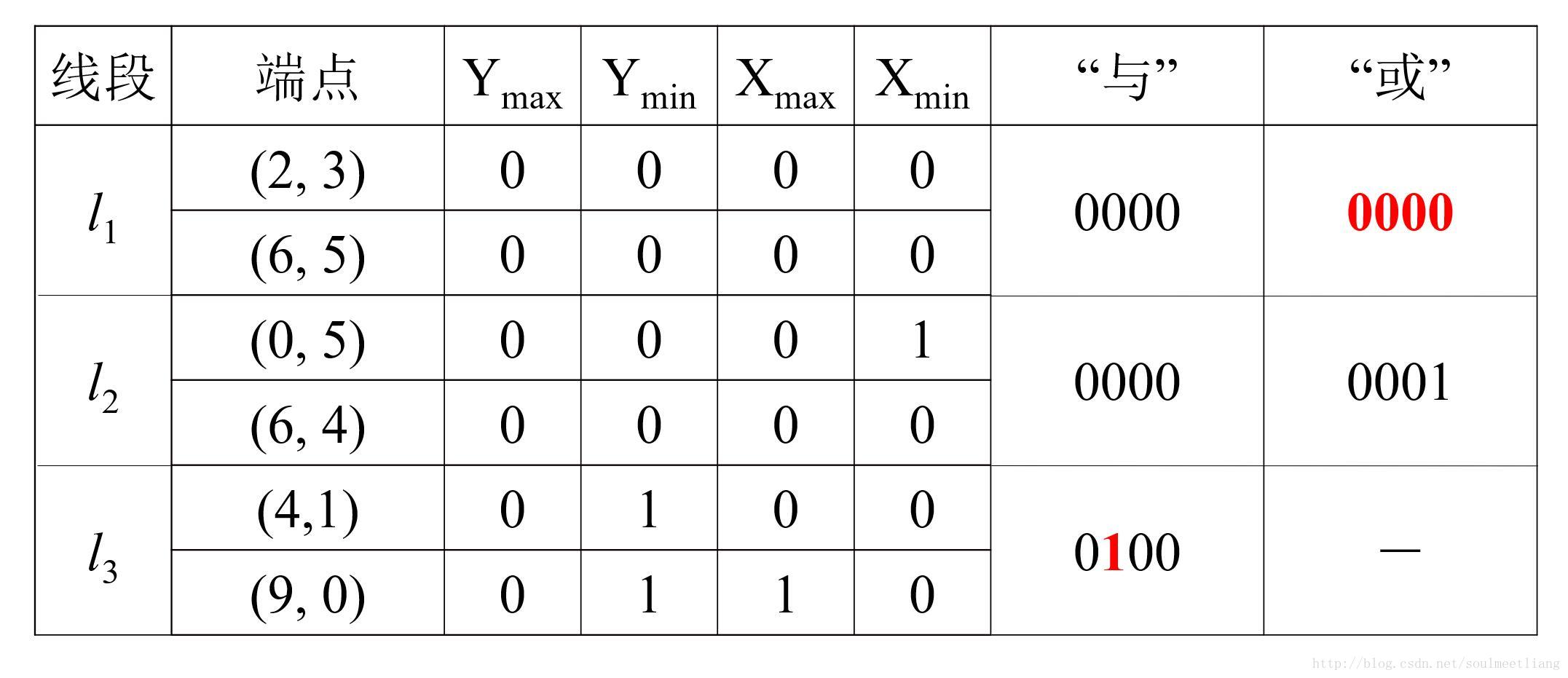
• 視窗內部的點根據兩端點編碼的“或”運算直接判定：
  
  • 0000 0000 －> 0000 邏輯或
• 大部分視窗外側的直線段可以根據兩端點編碼的“與”運算直接判定：
  
  • 1010 0010 －> 0010 邏輯與

求交

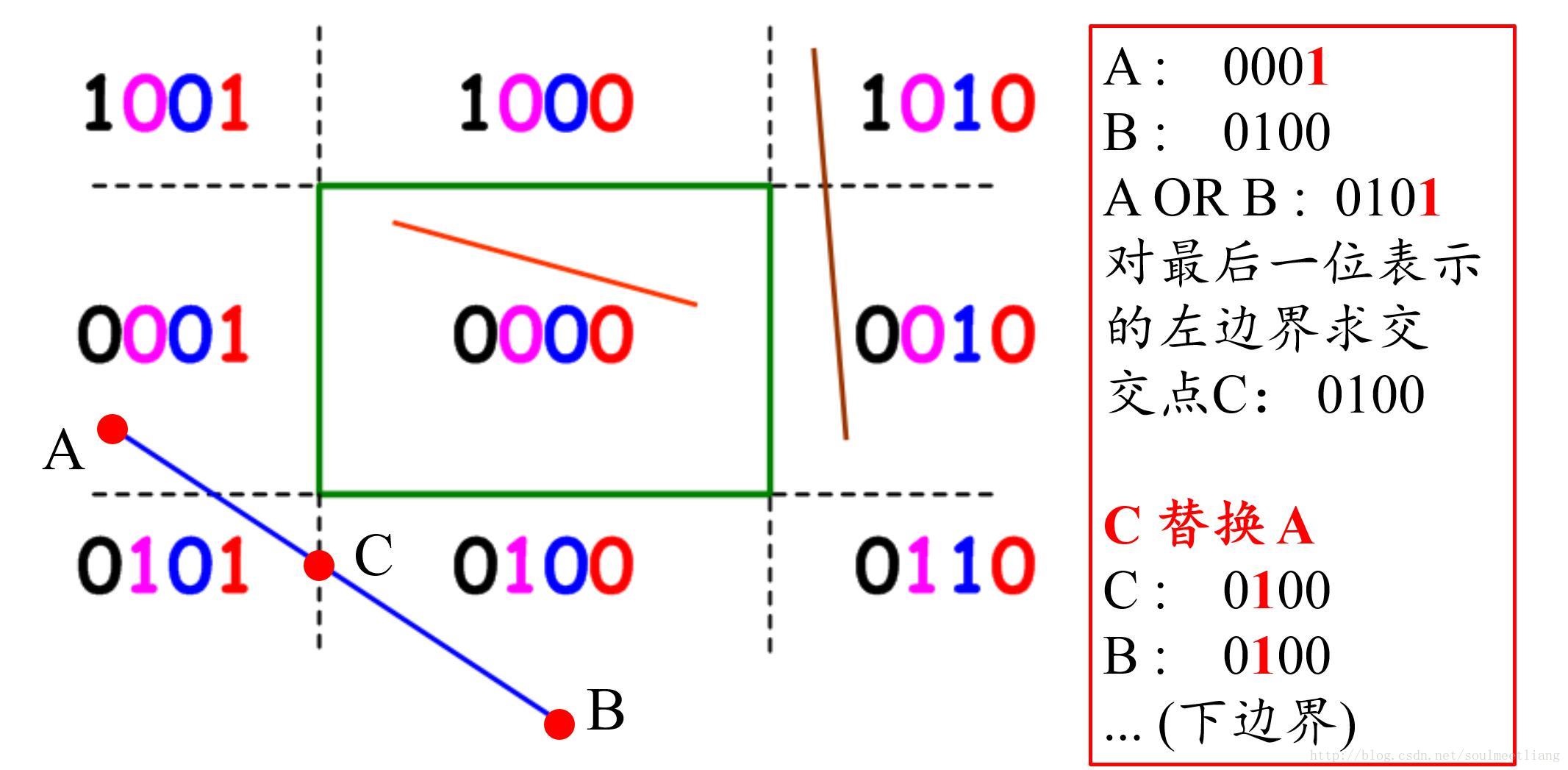
• 對於不能直接排除的直線段，我們需要計算交點。
• 在 Cohen-Sutherland 演算法中，計算交點是根據編碼資訊確定的，只有當“或”運算結果為 1 的編碼位對應的視窗邊界才需要計算交點。
• 如前面的例子中，藍色直線段不能直接排除，需要計算交點。此時觀察其兩個端點的編碼：

計算

虛實

• 當計算出一個直線段與視窗邊界的交點後，我們需要將新計算出的交點替換掉原來此編碼位出現 1 的端點。然後與另一端點繼續進行“或”運算來判定是否需要計算交點。
• 需要進行上述替換並繼續計算交點的原因，是計算出的交點可能是虛交點。
• 只有當最後進行邏輯或判定的兩個交點(或端點)最後的或運算結果為 0000 時，整個過程結束。
  

演算法

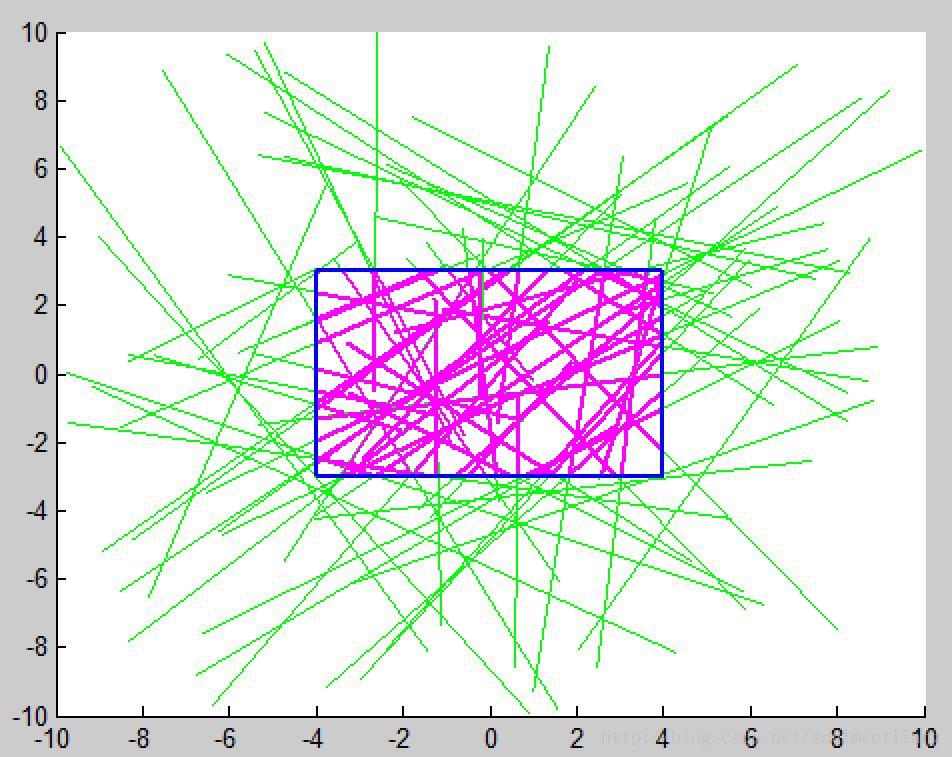
示例

Matlab程式碼

clear all;

n = 100;
Xmin = -4; Xmax = 4;
Ymin = -3; Ymax = 3;

figure; hold on;

P1x = rand(1,n)*20 - 10;  
P2x = rand(1,n)*20 - 10;
P1y = rand(1,n)*20 - 10;  
P2y = rand(1,n)*20 - 10;
P1code = zeros
 
(n,4);
P2code = zeros(n,4);

for i = 1:n    

    if P1x(i) < Xmin
        P1code(i,1) = 1;
    end
    if P1x(i) > Xmax
        P1code(i,2) = 1;
    end
    if P1y(i) < Ymin
        P1code(i,3) = 1;
    end
    if P1y(i) > Ymax
        P1code(i,4) = 1;
    end    

    if P2x(i) < Xmin
        P2code(i,1) = 1;
    end
    if P2x(i) > Xmax
        P2code(i,2) = 1;
    end
    if P2y(i) < Ymin
        P2code(i,3) = 1;
    end
    if P2y(i) > Ymax
        P2code(i,4) = 1;
    end

    plot([P1x(i),P2x(i)],[P1y(i),P2y(i)],'b-');
end
hold off;

P_label = zeros(1,n);
figure; hold on;
for i = 1:n
    P_or = P1code(i,1:4) | P2code(i,1:4);
    if sum(P_or) == 0
        P_label(i) = 1;
        plot([P1x(i),P2x(i)],[P1y(i),P2y(i)],'r-');
    end
    P_and = P1code(i,1:4) & P2code(i,1:4);
    if sum(P_and) > 0
        P_label(i) = 2;
        plot([P1x(i),P2x(i)],[P1y(i),P2y(i)],'g-');
    end
end
hold off;

figure; hold on;
for i = 1:n
    if P_label(i) == 0

        P_or = P1code(i,1:4) | P2code(i,1:4);
        plot([P1x(i),P2x(i)],[P1y(i),P2y(i)],'g-');

        if P_or(1) == 1
            Py = P1y(i) + (Xmin-P1x(i))*(P2y(i)-P1y(i))/(P2x(i)-P1x(i));
            if P1x(i) < Xmin
                P1x(i) = Xmin; P1y(i) = Py;
            elseif P2x(i) < Xmin
                P2x(i) = Xmin; P2y(i) = Py;
            end            
        end

        if P_or(2) == 1
            Py = P1y(i) + (Xmax-P1x(i))*(P2y(i)-P1y(i))/(P2x(i)-P1x(i));
            if P1x(i) > Xmax
                P1x(i) = Xmax; P1y(i) = Py;
            elseif P2x(i) > Xmax
                P2x(i) = Xmax; P2y(i) = Py;
            end            
        end

        if P_or(3) == 1
            Px = P1x(i) + (Ymin-P1y(i))/(P2y(i)-P1y(i))*(P2x(i)-P1x(i));
            if P1y(i) < Ymin
                P1x(i) = Px; P1y(i) = Ymin;
            elseif P2y(i) < Ymin
                P2x(i) = Px; P2y(i) = Ymin;
            end            
        end

        if P_or(4) == 1
            Px = P1x(i) + (Ymax-P1y(i))/(P2y(i)-P1y(i))*(P2x(i)-P1x(i));
            if P1y(i) > Ymax
                P1x(i) = Px; P1y(i) = Ymax;
            elseif P2y(i) > Ymax
                P2x(i) = Px; P2y(i) = Ymax;
            end            
        end
        if P1x(i) >= Xmin & P1x(i) <= Xmax & ...
                P2x(i) >= Xmin & P2x(i) <= Xmax & ...
                P1y(i) >= Ymin & P1y(i) <= Ymax & ...
                P2y(i) >= Ymin & P2y(i) <= Ymax
            plot([P1x(i),P2x(i)],[P1y(i),P2y(i)],'m-','LineWidth',2);
        end
        plot([-4 4 4 -4 -4],[-3 -3 3 3 -3],'b-','LineWidth',2);
    end
end
hold off;