神經網路技術起源於上世紀五、六十年代，當時叫感知機（perceptron），擁有輸入層、輸出層和一個隱含層。輸入的特徵向量通過隱含層變換達到輸出層，在輸出層得到分類結果。早期感知機的推動者是Rosenblatt。（扯一個不相關的：由於計算技術的落後，當時感知器傳輸函式是用線拉動變阻器改變電阻的方法機械實現的，腦補一下科學家們扯著密密麻麻的導線的樣子…）
但是，Rosenblatt的單層感知機有一個嚴重得不能再嚴重的問題，即它對稍複雜一些的函式都無能為力（比如最為典型的“異或”操作）。連異或都不能擬合，你還能指望這貨有什麼實際用途麼o(╯□╰)o

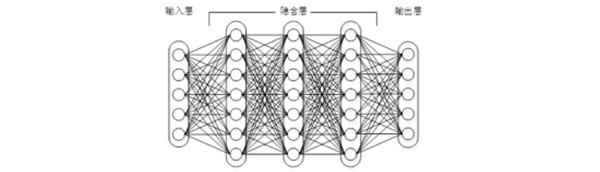
隨著數學的發展，這個缺點直到上世紀八十年代才被Rumelhart、Williams、Hinton、LeCun等人（反正就是一票大牛）發明的多層感知機（multilayer perceptron）克服。多層感知機，顧名思義，就是有多個隱含層的感知機（廢話……）。好好，我們看一下多層感知機的結構：

圖1上下層神經元全部相連的神經網路——多層感知機

多層感知機可以擺脫早期離散傳輸函式的束縛，使用sigmoid或tanh等連續函式模擬神經元對激勵的響應，在訓練演算法上則使用Werbos發明的反向傳播BP演算法。對，這貨就是我們現在所說的神經網路NN——神經網路聽起來不知道比感知機高階到哪裡去了！這再次告訴我們起一個好聽的名字對於研（zhuang）究（bi）很重要！

多層感知機解決了之前無法模擬異或邏輯的缺陷，同時更多的層數也讓網路更能夠刻畫現實世界中的複雜情形。相信年輕如Hinton當時一定是春風得意。

多層感知機給我們帶來的啟示是，神經網路的層數直接決定了它對現實的刻畫能力——利用每層更少的神經元擬合更加複雜的函式[1]。
（Bengio如是說：functions that can be compactly represented by a depth k architecture might require an exponential number of computational elements to be represented by a depth k − 1 architecture.）

即便大牛們早就預料到神經網路需要變得更深，但是有一個夢魘總是縈繞左右。隨著神經網路層數的加深，優化函式越來越容易陷入區域性最優解，並且這個“陷阱”越來越偏離真正的全域性最優。利用有限資料訓練的深層網路，效能還不如較淺層網路。同時，另一個不可忽略的問題是隨著網路層數增加，“梯度消失”現象更加嚴重。具體來說，我們常常使用sigmoid作為神經元的輸入輸出函式。對於幅度為1的訊號，在BP反向傳播梯度時，每傳遞一層，梯度衰減為原來的0.25。層數一多，梯度指數衰減後低層基本上接受不到有效的訓練訊號。

2006年，Hinton利用預訓練方法緩解了區域性最優解問題，將隱含層推動到了7層[2]，神經網路真正意義上有了“深度”，由此揭開了深度學習的熱潮。這裡的“深度”並沒有固定的定義——在語音識別中4層網路就能夠被認為是“較深的”，而在影象識別中20層以上的網路屢見不鮮。為了克服梯度消失，ReLU、maxout等傳輸函式代替了sigmoid，形成了如今DNN的基本形式。單從結構上來說，全連線的DNN和圖1的多層感知機是沒有任何區別的。

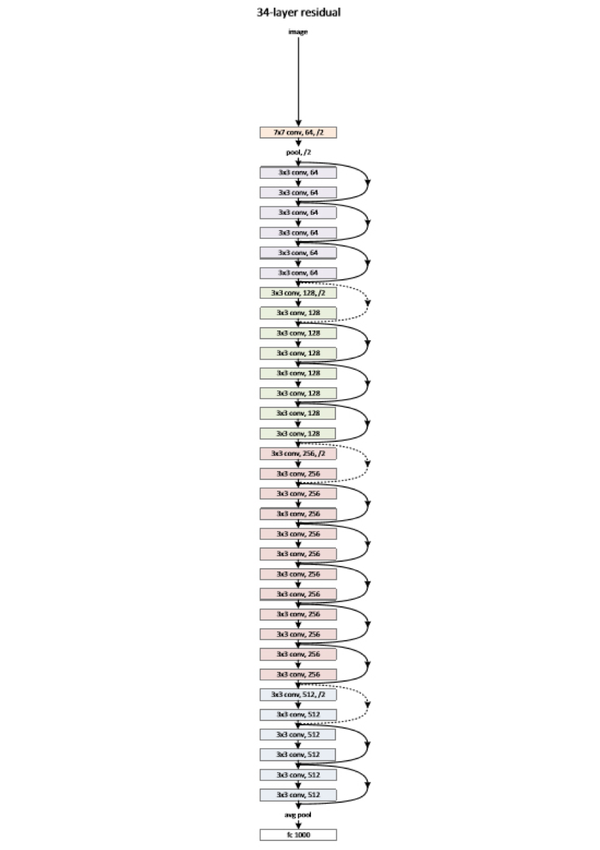
值得一提的是，今年出現的高速公路網路（highway network）和深度殘差學習（deep residual learning）進一步避免了梯度消失，網路層數達到了前所未有的一百多層（深度殘差學習：152層）[3,4]！具體結構題主可自行搜尋瞭解。如果你之前在懷疑是不是有很多方法打上了“深度學習”的噱頭，這個結果真是深得讓人心服口服。

圖2縮減版的深度殘差學習網路，僅有34層，終極版有152層，自行感受一下

如圖1所示，我們看到全連線DNN的結構裡下層神經元和所有上層神經元都能夠形成連線，帶來的潛在問題是引數數量的膨脹。假設輸入的是一幅畫素為1K*1K的影象，隱含層有1M個節點，光這一層就有10^12個權重需要訓練，這不僅容易過擬合，而且極容易陷入區域性最優。另外，影象中有固有的區域性模式（比如輪廓、邊界，人的眼睛、鼻子、嘴等）可以利用，顯然應該將影象處理中的概念和神經網路技術相結合。此時我們可以祭出題主所說的卷積神經網路CNN。對於CNN來說，並不是所有上下層神經元都能直接相連，而是通過“卷積核”作為中介。同一個卷積核在所有影象內是共享的，影象通過卷積操作後仍然保留原先的位置關係。兩層之間的卷積傳輸的示意圖如下：

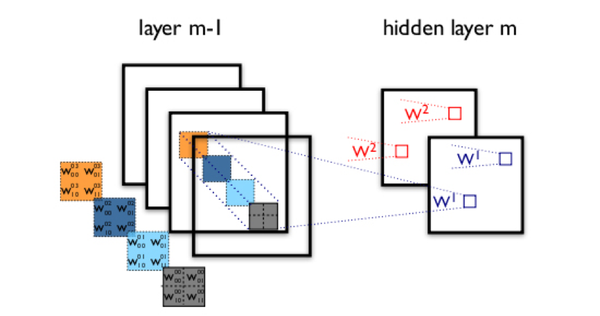
圖3卷積神經網路隱含層（摘自Theano教程）

通過一個例子簡單說明卷積神經網路的結構。假設圖3中m-1=1是輸入層，我們需要識別一幅彩色影象，這幅影象具有四個通道ARGB（透明度和紅綠藍，對應了四幅相同大小的影象），假設卷積核大小為100*100，共使用100個卷積核w1到w100（從直覺來看，每個卷積核應該學習到不同的結構特徵）。用w1在ARGB影象上進行卷積操作，可以得到隱含層的第一幅影象；這幅隱含層影象左上角第一個畫素是四幅輸入影象左上角100*100區域內畫素的加權求和，以此類推。同理，算上其他卷積核，隱含層對應100幅“影象”。每幅影象對是對原始影象中不同特徵的響應。按照這樣的結構繼續傳遞下去。CNN中還有max-pooling等操作進一步提高魯棒性。

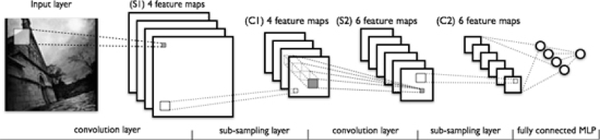
圖4一個典型的卷積神經網路結構，注意到最後一層實際上是一個全連線層（摘自Theano教程）

在這個例子裡，我們注意到輸入層到隱含層的引數瞬間降低到了100*100*100=10^6個！這使得我們能夠用已有的訓練資料得到良好的模型。題主所說的適用於影象識別，正是由於CNN模型限制引數了個數並挖掘了局部結構的這個特點。順著同樣的思路，利用語音語譜結構中的區域性資訊，CNN照樣能應用在語音識別中。

全連線的DNN還存在著另一個問題——無法對時間序列上的變化進行建模。然而，樣本出現的時間順序對於自然語言處理、語音識別、手寫體識別等應用非常重要。對了適應這種需求，就出現了題主所說的另一種神經網路結構——迴圈神經網路RNN。

在普通的全連線網路或CNN中，每層神經元的訊號只能向上一層傳播，樣本的處理在各個時刻獨立，因此又被成為前向神經網路(Feed-forward Neural Networks)。而在RNN中，神經元的輸出可以在下一個時間戳直接作用到自身，即第i層神經元在m時刻的輸入，除了（i-1）層神經元在該時刻的輸出外，還包括其自身在（m-1）時刻的輸出！表示成圖就是這樣的：

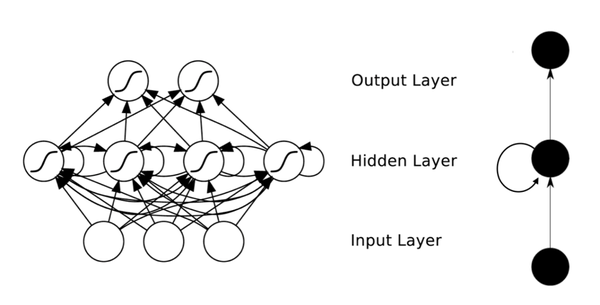
圖5 RNN網路結構

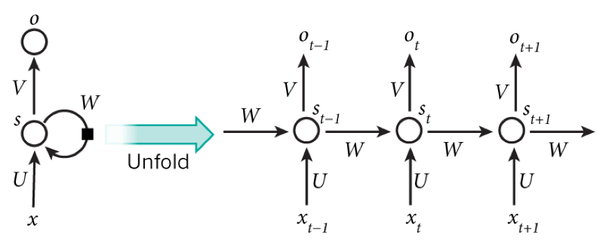
我們可以看到在隱含層節點之間增加了互連。為了分析方便，我們常將RNN在時間上進行展開，得到如圖6所示的結構：

圖6 RNN在時間上進行展開

Cool，（t+1）時刻網路的最終結果O(t+1)是該時刻輸入和所有歷史共同作用的結果！這就達到了對時間序列建模的目的。

不知題主是否發現，RNN可以看成一個在時間上傳遞的神經網路，它的深度是時間的長度！正如我們上面所說，“梯度消失”現象又要出現了，只不過這次發生在時間軸上。對於t時刻來說，它產生的梯度在時間軸上向歷史傳播幾層之後就消失了，根本就無法影響太遙遠的過去。因此，之前說“所有歷史”共同作用只是理想的情況，在實際中，這種影響也就只能維持若干個時間戳。

為了解決時間上的梯度消失，機器學習領域發展出了長短時記憶單元LSTM，通過門的開關實現時間上記憶功能，並防止梯度消失，一個LSTM單元長這個樣子：

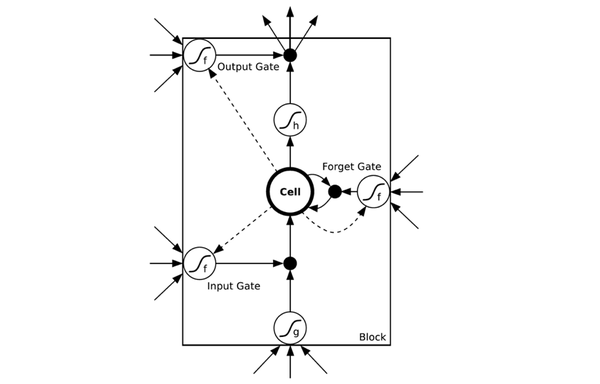
圖7 LSTM的模樣

除了題主疑惑的三種網路，和我之前提到的深度殘差學習、LSTM外，深度學習還有許多其他的結構。舉個例子，RNN既然能繼承歷史資訊，是不是也能吸收點未來的資訊呢？因為在序列訊號分析中，如果我能預知未來，對識別一定也是有所幫助的。因此就有了雙向RNN、雙向LSTM，同時利用歷史和未來的資訊。

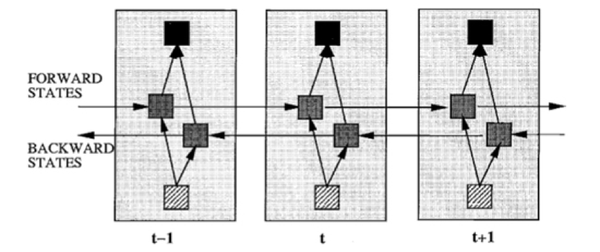
圖8雙向RNN

事實上，不論是那種網路，他們在實際應用中常常都混合著使用，比如CNN和RNN在上層輸出之前往往會接上全連線層，很難說某個網路到底屬於哪個類別。不難想象隨著深度學習熱度的延續，更靈活的組合方式、更多的網路結構將被髮展出來。儘管看起來千變萬化，但研究者們的出發點肯定都是為了解決特定的問題。題主如果想進行這方面的研究，不妨仔細分析一下這些結構各自的特點以及它們達成目標的手段。入門的話可以參考：
Ng寫的Ufldl：UFLDL教程 - Ufldl
也可以看Theano內自帶的教程，例子非常具體：Deep Learning Tutorials
歡迎大家繼續推薦補充。
當然啦，如果題主只是想湊個熱鬧時髦一把，或者大概瞭解一下方便以後把妹使，這樣看看也就罷了吧。

參考文獻：
[1] Bengio Y. Learning Deep Architectures for AI[J]. Foundations & Trends® in Machine Learning, 2009, 2(1):1-127.
[2] Hinton G E, Salakhutdinov R R. Reducing the Dimensionality of Data with Neural Networks[J]. Science, 2006, 313(5786):504-507.
[3] He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. arXiv:1512.03385, 2015.
[4] Srivastava R K, Greff K, Schmidhuber J. Highway networks. arXiv:1505.00387, 2015.

【“科研君”公眾號初衷始終是希望聚集各專業一線科研人員和工作者，在進行科學研究的同時也作為知識的傳播者，利用自己的專業知識解釋和普及生活中的 一些現象和原理，展現科學有趣生動的一面。該公眾號由清華大學一群在校博士生髮起，目前參與的作者人數有10人，但我們感覺這遠遠不能覆蓋所以想科普的領域，並且由於空閒時間有限，導致我們只能每週釋出一篇文章。我們期待更多的戰友加入，認識更多志同道合的人，每個人都是科研君，每個人都是知識的傳播者。我們期待大家的參與，想加入我們，進QQ群吧~：108141238】

【非常高興看到大家喜歡並贊同我們的回答。應許多知友的建議，最近我們開通了同名公眾號：PhDer，也會定期更新我們的文章，如果您不想錯過我們的每篇回答，歡迎掃碼關注~ 】