在Leetcode刷Single Number這道題的時候，自己的想法就是遍歷，想了下別的簡便想法，楞是沒想出，看了下討論區的大手的，發現了使用XOR，於是想著補補門陣列了。

Given a non-empty array of integers, every element appears twice except for one. Find that single one.

Example 1:

Input: [2,2,1]  Output: 1

異或運算子（^）

參加運算的兩個資料，按二進位制位進行“異或”運算 

運算規則：0^0=0；  0^1=1；  1^0=1；   1^1=0；即：參加運算的兩個物件，如果兩個相應位為“異”（值不同），則該位結果為1，否則為0。

“異或運算”的特殊作用：

（1）使特定位翻轉找一個數，對應X要翻轉的各位，該數的對應位為1，其餘位為零，此數與X對應位異或即可。

例：X=10101110，使X低4位翻轉，用X ^0000 1111 = 1010 0001即可得到。

（2）與0相異或，保留原值 ，X ^ 00000000 = 1010 1110。

其他規律有：

（1）將兩數異或的結果與其中一數再進行異或，可以得到另一個數。

例：11^01=10 ； 11^10=01

原理很簡單，兩數異或的結果儲存了兩個數上每一個二進位制位不同或相同的資訊，如果相應的二進位制位不同，就標誌為1，如果相同，則標誌為0。

我們可以利用這個特點交換兩個數：

temp=a^b;
a=temp^a;
b=temp^b;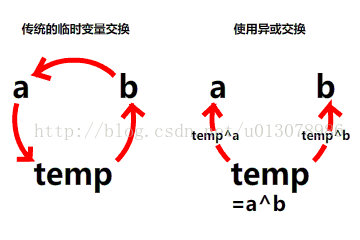

但是使用這種方法似乎與使用臨時變數沒有什麼區別？其實不然，通過簡單分析可以發現臨時變數的值在整個過程中並沒有發生變化，因此也可以無需設定臨時變數。

a=a^b^a;
b=a^b^b;

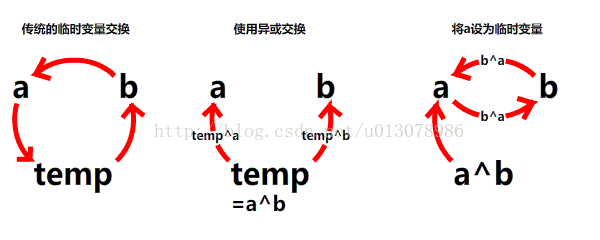
a=a^b;
b=b^a;
a=b^a;

 還可以寫得更簡潔一點：

a^=b^=a^=b;

還可以通過加減實現兩數互換：

a=a+b
b=a-b;
a=a-b;

前提是a+b的值不能溢位。

（2）一個數與另一個數異或兩次是其本身 

8^9^9=8

按位與運算子（&）

參加運算的兩個資料，按二進位制位進行“與”運算。

運算規則：0&0=0;  0&1=0;   1&0=0;    1&1=1;

      即：兩位同時為“1”，結果才為“1”，否則為0

例如：3&5  即 0000 0011& 0000 0101 = 00000001  因此，3&5的值得1。

另，負數按補碼形式參加按位與運算。

“與運算”的特殊用途：

（1）清零。如果想將一個單元清零，即使其全部二進位制位為0，只要與一個各位都為零的數值相與，結果為零。

（2）取一個數中指定位

方法：找一個數，對應X要取的位，該數的對應位為1，其餘位為零，此數與X進行“與運算”可以得到X中的指定位。

例：設X=10101110，取X的低4位，用 X & 0000 1111 = 00001110 即可得到；

        還可用來取X的2、4、6位。

（3）保留指定位

與一個數進行“按位與”運算，此數在該位取1.

例如：有一數84，即01010100，想把其中從左邊算起的第3，4，5，7，8位保留下來

01010100

&

00111011

—————
00010000

按位或運算子（|）

參加運算的兩個物件，按二進位制位進行“或”運算。

運算規則：0|0=0；  0|1=1；  1|0=1；   1|1=1；

     即 ：參加運算的兩個物件只要有一個為1，其值為1。

例如:3|5　即 00000011 | 0000 0101 = 00000111  因此，3|5的值得7。　

另，負數按補碼形式參加按位或運算。

“或運算”特殊作用：

（1）常用來對一個數據的某些位置1。

方法：找到一個數，對應X要置1的位，該數的對應位為1，其餘位為零。此數與X相或可使X中的某些位置1。

例：將X=10100000的低4位置1 ，用X | 0000 1111 = 1010 1111即可得到。

https://blog.csdn.net/xhmj12/article/details/81114436

https://blog.csdn.net/xiaopihaierletian/article/details/78162863