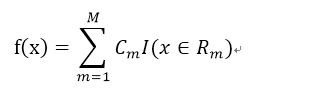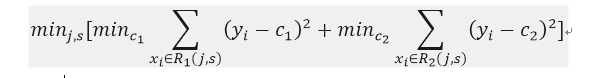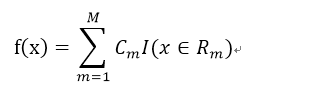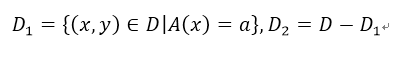這一篇主要是CART，有幾個重點的詞語先寫下來，重點哦：基尼指數(Gini index)、最小二乘迴歸樹(least squares regression tree)
CART：classification and regression tree。分類迴歸樹。
簡單的說呢，CART就是個二叉樹(廣義的決策樹並不一定就是二叉樹，可能好幾叉。。。哈哈)，所以內部節點的取值就是“是”“否”的了。
直接介紹演算法吧，CART的基本原理和廣義的決策樹是一樣的，就相當於二叉樹都有普通樹的特徵。

下面直接介紹迴歸樹的演算法：
1. 迴歸樹的生成：基於訓練資料集生成決策樹，儘量大點。
2. 迴歸樹剪枝：用驗證資料集對已生成的樹進行剪枝並選擇最優子樹，這時用損失函式最小作為剪枝的標準。
完了，，，很簡單的。哈哈

下面介紹一下詳細的演算法，重點還是大多參考了統計學習方法的：
簡單介紹一下理論：給定資料集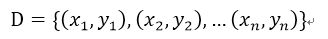
假設已經將輸入空間劃分為M個單元R_1、R_2、…R_M，並且每個單元都有一個固定的輸出值C_m，則迴歸樹的模型為：

訓練資料集的預測誤差為：平方誤差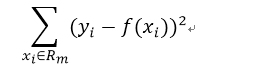
平方誤差是用來球每個單元上的最優輸出值
即：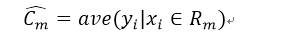
那麼怎麼選擇劃分的那條線呢？
選擇第j個變數x_j和取得值s，定義兩個區域：

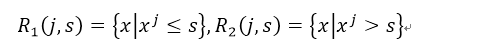
那麼在這裡我們就尋找最優的j和s，也就是求解：

書上是這樣的，但是我感覺中括號裡的兩個min就不要了。刪掉就好。
求解的過程待會見迴歸樹生成演算法。

通常，通過以上過程建立的迴歸樹叫做最小二乘迴歸樹。
最小二乘迴歸樹的生成演算法：
輸入：訓練資料集D
輸出：迴歸樹f(x)
在訓練資料集所在的輸入空間中，遞迴的將每個區域劃分為兩個子區域並決定每個子區域上的輸出值，構建二車決策樹：
1）. 選擇最優劃分變數j和s；
求解：

遍歷變數j，對固定的j掃描s，選擇是上式最小值的(j,s);
2）. 用選定的(j,s)劃分區域並決定相應的輸出值；


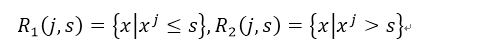
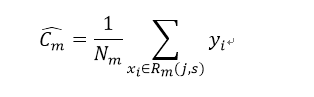
3）. 繼續1）、2）步驟，直至滿足條件；
4）.將輸入空間劃為M個區域，R_1…….R_m，生成決策樹：

接下來是什麼呢？上邊是迴歸，下邊就是分類了，分類樹的生成是怎麼做的呢？
最開始的基尼指數就要開始登場了：
分類樹是通過基尼指數來選擇最優特徵的，同時決定該特徵的最優切分點。
基尼指數：假設有k個類，樣本屬於第k個類的概率為P_k, 則此概率分佈的基尼指數定義為：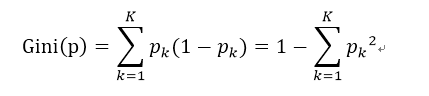
對於給定的離散資料集D, 其基尼指數為：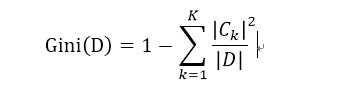
如果樣本集合D根據特徵A是否去某一個值a被分割為D_1、D_2，
即：

那麼這就是在特徵A的條件下D的基尼指數是：

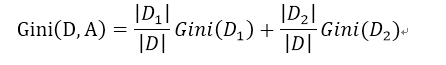
基尼指數求出來了，那麼基尼指數有什麼意義呢？
基尼指數表示集合D的不確定性，基尼指數 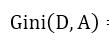表示經過特徵A分割後D的不確定性，跟條件熵是不是很相似。。。Gini(D)和熵也是很類似的。
CART的分類樹生成演算法：
輸入： 訓練資料集D，停止計算的條件。
輸出： CART決策樹.
根據訓練資料集，從根節點開始，遞迴的對每一個結點進行以下操作，構建決策樹。
1. 設結點的訓練集為D，計算現有特徵對該資料集的基尼指數，此時，對每一個特徵A，對其可能取的每一個值a，根據樣本點對A=a的測試是“是”還是“否”，將D分割成D_1,D_2，利用上邊的式子計算A=a時的基尼指數。
2. 在所有可能的特徵A以及它們所有可能的切分點a中，選擇基尼指數最小的特徵及其對應的切分點作為最優特徵與最優切分點（基尼指數越大不確定性越大，不好，所以選小的）。依最優特徵與最優切分點，從現結點生成兩個子結點，將訓練資料集依特徵分配到兩個子結點中去。
3. 對兩個子結點遞迴的呼叫步驟1. 2.直至滿足條件。
4. 生成CART決策樹。
演算法停止的條件是結點中的樣本個數小於預定閾值，或樣本的基尼指數小於預定閾值(樣本基本屬於同一類)，或者沒有更多特徵了。

完了。。。。。這就是分類迴歸樹的理論原理，還剩了個剪枝沒記錄，但是剪枝就涉及自己實現的時候用到的，等以後自己實現的時候用到了再詳細解釋吧。下一個是隨機森林和隨機蕨。