簡單易學的機器學習演算法——分類迴歸樹CART
阿新 • • 發佈:2019-02-11
引言
分類迴歸樹(Classification and Regression Tree,CART)是一種典型的決策樹演算法,CART演算法不僅可以應用於分類問題,而且可以用於迴歸問題。
一、樹迴歸的概念
對於一般的線性迴歸,其擬合的模型是基於全部的資料集。這種全域性的資料建模對於一些複雜的資料來說,其建模的難度也會很大。其後,我們有了區域性加權線性迴歸,其只利用資料點周圍的區域性資料進行建模,這樣就簡化了建模的難度,提高了模型的準確性。樹迴歸也是一種區域性建模的方法,其通過構建決策點將資料切分,在切分後的區域性資料集上做迴歸操作。 在博文“簡單易學的機器學習演算法——決策樹之ID3演算法二、迴歸樹的分類
在構建迴歸樹時,主要有兩種不同的樹:- 迴歸樹(Regression Tree),其每個葉節點是單個值
- 模型樹(Model Tree),其每個葉節點是一個線性方程
三、基於CART演算法的迴歸樹
在進行樹的左右子樹劃分時,有一個很重要的量,即給定的值,特徵值大於這個給定的值的屬於一個子樹,小於這個給定的值的屬於另一個子樹。這個給定的值的選取的原則是使得劃分後的子樹中的“混亂程度”降低。如何定義這個混亂程度是設計CART演算法的一個關鍵的地方。在ID3演算法中我們使用的資訊熵和資訊增益的概念。資訊熵就代表了資料集的紊亂程度。對於連續型的問題,我們可以使用方差的概念來表達混亂程度,方差越大,越紊亂。所以我們要找到使得切分之後的方差最小的劃分方式。四、實驗模擬
對於資料集1,資料集2,我們分別使用CART演算法構建迴歸樹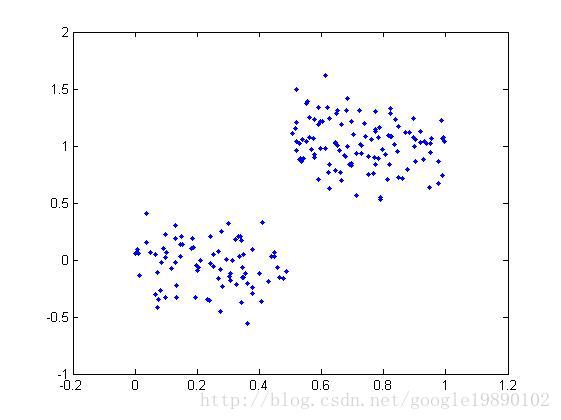
(資料集1)
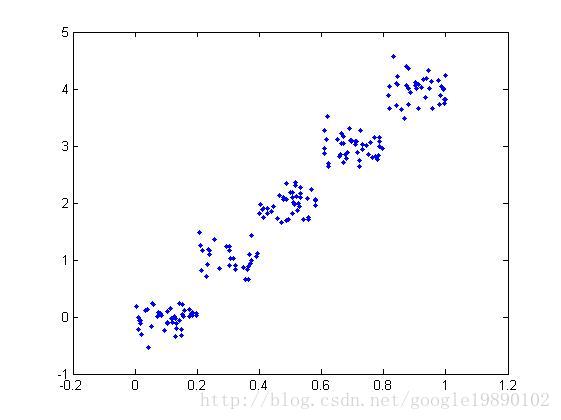
(資料集2)從圖上我們可以看出可以將資料集劃分成兩個子樹,即左右子樹,並分別在左右子樹上做線性迴歸。同樣的道理,下圖可以劃分為5個子樹。
結果為:
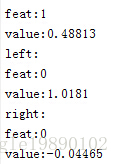
(資料集1的結果)
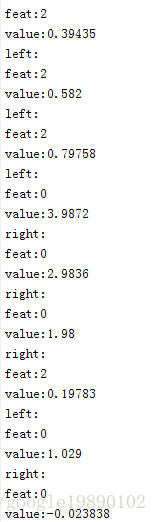
(資料集2的結果)
MATLAB程式碼:
主程式%% CART
clear all
clc
% 匯入資料集
%dataSet = load('ex00.txt');
dataSet = load('ex0.txt');
% 畫圖1
% plot(dataSet(:,1),dataSet(:,2),'.');
% axis([-0.2,1.2,-1.0,2.0]);
% 畫圖2
% plot(dataSet(:,2),dataSet(:,3),'.');
% axis([-0.2,1.2,-1.0,5.0]);
createTree(dataSet,1,4);
構建子樹
function [ retTree ] = createTree( dataSet,tolS,tolN )
[feat,val] = chooseBestSplit(dataSet, tolS, tolN);
disp(['feat:', num2str(feat)]);
disp(['value:', num2str(val)]);
if feat == 0
return;
end
[lSet,rSet] = binSplitDataSet(dataSet, feat, val);
disp('left:');
createTree( lSet,tolS,tolN );
disp('right:');
createTree( rSet,tolS,tolN );
end
最佳劃分
function [ Index, Value ] = chooseBestSplit( dataSet, tolS, tolN )
% 引數中tolS是容許的誤差下降值,tolN是切分的最小樣本數
m = size(dataSet);%資料集的大小
if length(unique(dataSet(:,m(:,2)))) == 1%僅剩下一種時
Index = 0;
Value = regLeaf(dataSet(:,m(:,2)));
return;
end
S = regErr(dataSet);%誤差
bestS = inf;%初始化,無窮大
bestIndex = 0;
bestValue = 0;
%找到最佳的位置和最優的值
for j = 1:(m(:,2)-1)%得到列
b = unique(dataSet(:,j));%得到特徵所在的列
lenCharacter = length(b);
for i = 1:lenCharacter
temp = b(i,:);
[mat0,mat1] = binSplitDataSet(dataSet, j ,temp);
m0 = size(mat0);
m1 = size(mat1);
if m0(:,1) < tolN || m1(:,1) < tolN
continue;
end
newS = regErr(mat0) + regErr(mat1);
if newS < bestS
bestS = newS;
bestIndex = j;
bestValue = temp;
end
end
end
if (S-bestS) < tolS
Index = 0;
Value = regLeaf(dataSet(:,m(:,2)));
return;
end
%劃分
[mat0, mat1] = binSplitDataSet(dataSet, bestIndex ,bestValue);
m0 = size(mat0);
m1 = size(mat1);
if m0(:,1) < tolN || m1(:,1) < tolN
Index = 0;
Value = regLeaf(dataSet(:,m(:,2)));
return;
end
Index = bestIndex;
Value = bestValue;
end
劃分
%% 將資料集劃分為兩個部分
function [ dataSet_1, dataSet_2 ] = binSplitDataSet( dataSet, feature, value )
[m,n] = size(dataSet);%計算資料集的大小
DataTemp = dataSet(:,feature)';%變成行
%計算行中標籤列的元素大於value的行
index_1 = [];%空的矩陣
index_2 = [];
for i = 1:m
if DataTemp(1,i) > value
index_1 = [index_1,i];
else
index_2 = [index_2,i];
end
end
[m_1,n_1] = size(index_1);%這裡要取列數
[m_2,n_2] = size(index_2);
if n_1>0 && n_2>0
for j = 1:n_1
dataSet_1(j,:) = dataSet(index_1(1,j),:);
end
for j = 1:n_2
dataSet_2(j,:) = dataSet(index_2(1,j),:);
end
elseif n_1 == 0
dataSet_1 = [];
dataSet_2 = dataSet;
elseif n_2 == 0
dataSet_2 = [];
dataSet_1 = dataSet;
end
end
%% 將資料集劃分為兩個部分
function [ dataSet_1, dataSet_2 ] = binSplitDataSet( dataSet, feature, value )
[m,n] = size(dataSet);%計算資料集的大小
DataTemp = dataSet(:,feature)';%變成行
%計算行中標籤列的元素大於value的行
index_1 = [];%空的矩陣
index_2 = [];
for i = 1:m
if DataTemp(1,i) > value
index_1 = [index_1,i];
else
index_2 = [index_2,i];
end
end
[m_1,n_1] = size(index_1);%這裡要取列數
[m_2,n_2] = size(index_2);
if n_1>0 && n_2>0
for j = 1:n_1
dataSet_1(j,:) = dataSet(index_1(1,j),:);
end
for j = 1:n_2
dataSet_2(j,:) = dataSet(index_2(1,j),:);
end
elseif n_1 == 0
dataSet_1 = [];
dataSet_2 = dataSet;
elseif n_2 == 0
dataSet_2 = [];
dataSet_1 = dataSet;
end
end
偏差
function [ error ] = regErr( dataSet )
m = size(dataSet);%求得dataSet的大小
dataVar = var(dataSet(:,m(:,2)));
error = dataVar * (m(:,1)-1);
end
葉節點
function [ leaf ] = regLeaf( dataSet )
m = size(dataSet);
leaf = mean(dataSet(:,m(:,2)));
end
