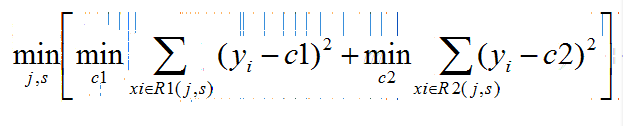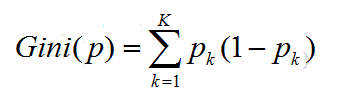CART演算法介紹：
分類和迴歸樹（CART）是應用廣泛的決策樹學習方法。CART同樣由特徵選擇，樹的生成和減枝組成，既可以用於分類也可以用於迴歸。CART的生成就是遞迴的構建二叉決策樹的過程。對迴歸樹用平方誤差最小化（RMSE），對分類樹用基尼指數最小化準則，進行特徵選擇，生成二叉樹。

1.迴歸樹生成的演算法介紹
輸入：訓練資料集D
輸出：迴歸樹f(x)
在訓練資料集所在的輸入空間中，遞迴的將每個區域劃分為兩個子區域並決定每個子區域的輸出值，構造二叉樹：
（1) 選擇最優切分特徵f和切分點s，求解

遍歷變數j，對固定特徵f掃描切分點，使公式達到最小

（2）用選定的特徵f和切分點s劃分區域，並決定輸出值：
每個區域的輸出值等於屬於該區域的目標值的均值

（3）繼續對兩個子區域呼叫步驟（1）（2），知道瞞住停止條件
（4）將輸入空間劃分成M個區域，生成決策樹

2，分類樹生成的演算法介紹
分類樹是用基尼指數選擇最優特徵，同時決定該特徵的最優切分點。
（基尼指數） 分類問題中，假設有K個類，樣本點屬於第k個類的概率為pk，則概率分佈的基尼指數定義為：

分類演算法：
根據訓練資料集，從根節點開始，遞迴的對每個節點進行以下操作，構建二叉樹：
（1）設節點的訓練資料集為D，計算現有特徵對該資料集的基尼指數，此時對每個特徵A，對其可能取得每個值a，更具樣本點對A=a將D分割為D1和D2兩部分，計算A=a的基尼指數
（2）對所有可能的特徵A以及對他們所有可能的切分點a，選擇基尼指數最小的特徵及對應的切分點作為最優特徵與最優切分點。依據最優特徵與最優切分切分點，將現節點切分為連個子節點。
（3）對兩個子節點，呼叫（1）（2），直至滿足停止條件
（4）生成CART決策樹

擴充套件：隨機森林就是由多棵CART（Classification And Regression Tree）構成的。對於每棵樹，它們使用的訓練集是從總的訓練集中有放回取樣出來的，這意味著，總的訓練集中的有些樣本可能多次出現在一棵樹的訓練集中，也可能從未出現在一棵樹的訓練集中。在訓練每棵樹的節點時，使用的特徵是從所有特徵中按照一定比例隨機地無放回的抽取的，根據Leo Breiman的建議，假設總的特徵數量為M，這個比例可以是sqrt(M),1/2sqrt(M),2sqrt(M)。

本blog內容參考了《統計學習方法》第五章決策樹的內容