評分卡模型-理論
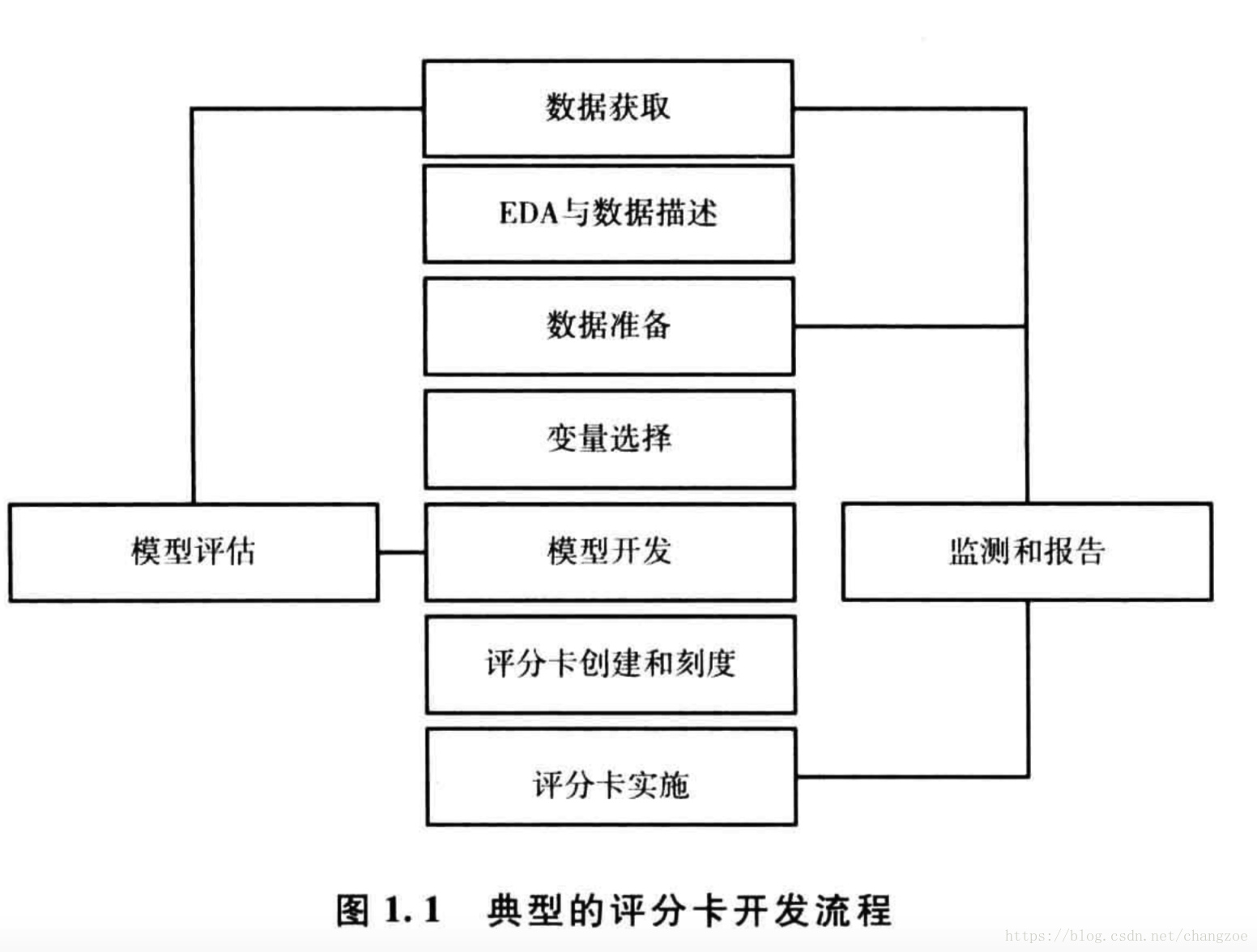
評分卡模型流程
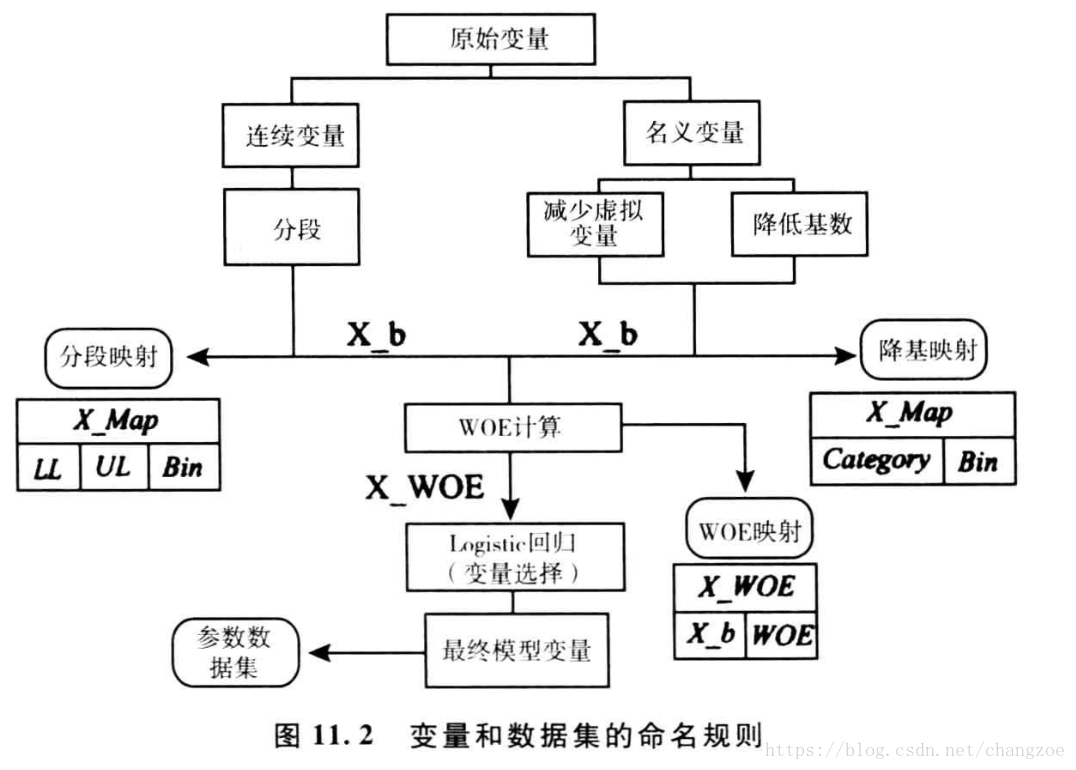
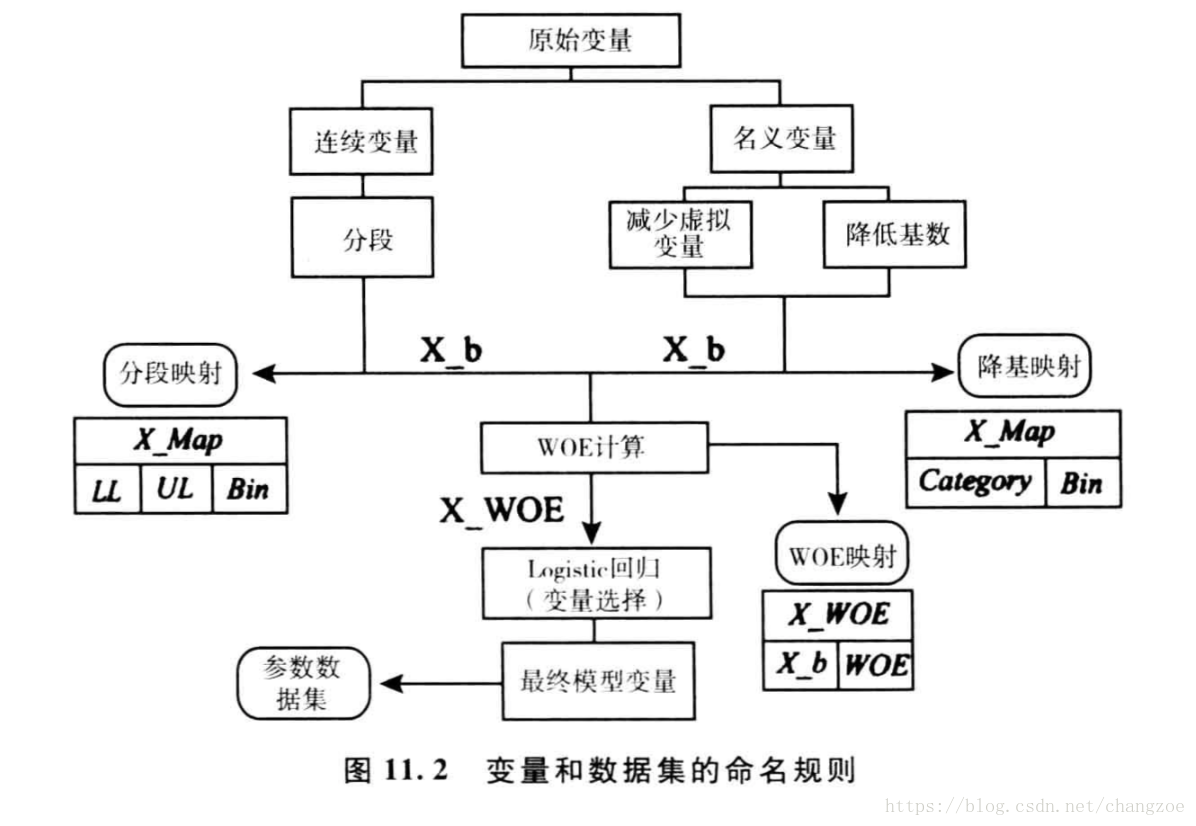
變數分群/分箱
通常是為了讓變數的預測力最強
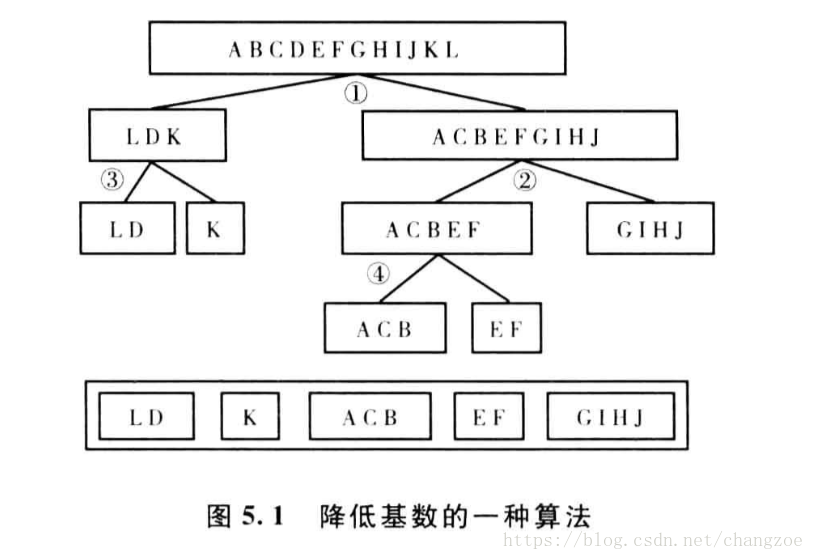
名義變數降低基數


類似決策樹的一種演算法
連續變數的分箱
在評分卡建模中,變數分箱(binning)是對連續變數離散化(discretization)的一種稱呼。要將logistic模型轉換為標準評分卡的形式,這一環節是必須完成的。信用評分卡開發中一般有常用的等距分段、等深分段、最優分段。
其中等距分段(Equval length intervals)是指分段的區間是一致的,比如年齡以十年作為一個分段;等深分段(Equal frequency intervals)是先確定分段數量,然後令每個分段中資料數量大致相等;最優分段(Optimal Binning)又叫監督離散化(supervised discretizaion),使用遞迴劃分(Recursive Partitioning)將連續變數分為分段,背後是一種基於條件推斷查詢較佳分組的演算法(Conditional Inference Tree)。
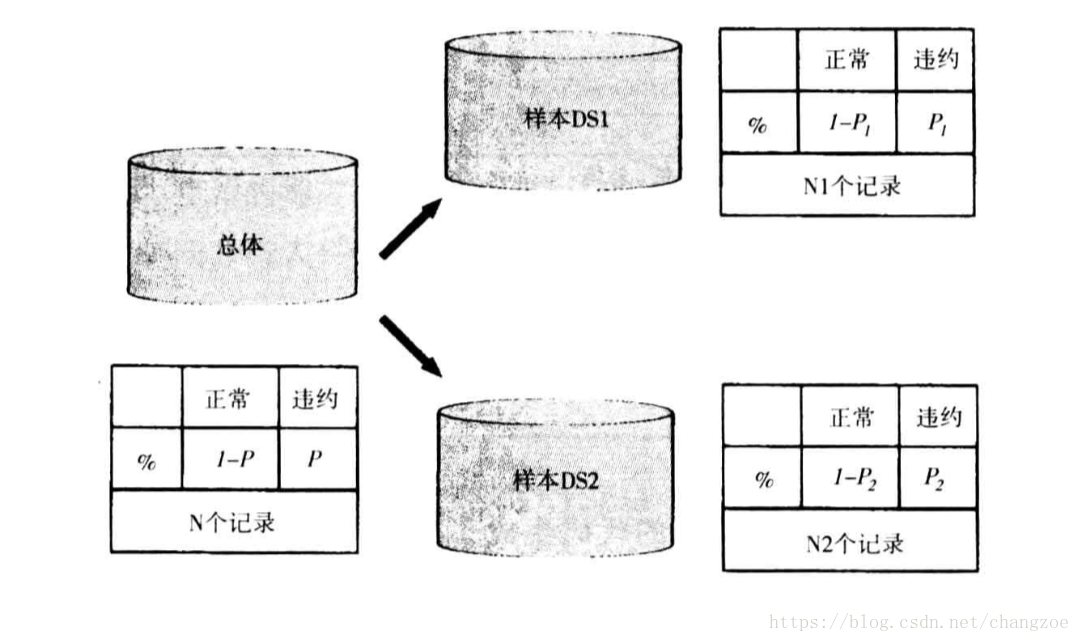
抽樣和權重計算
隨機抽樣
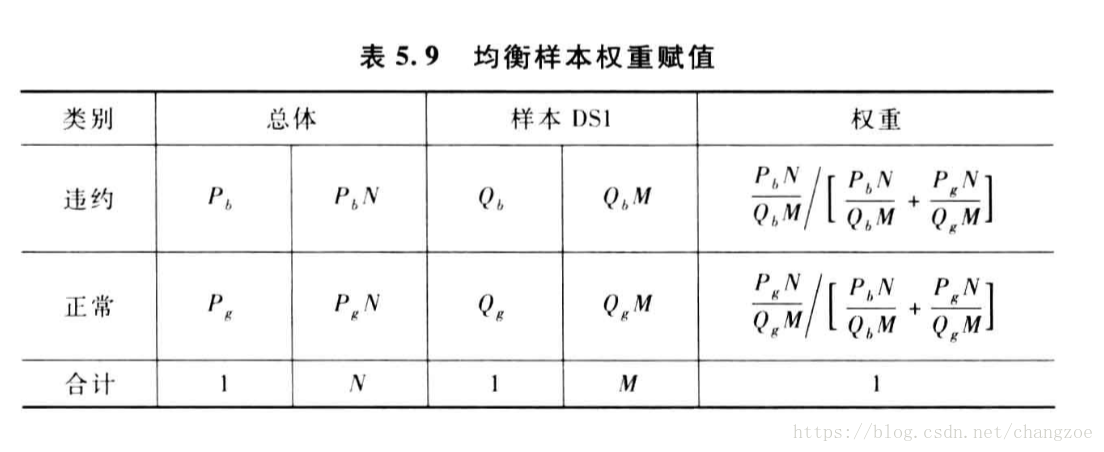
均衡抽樣
- 分層抽樣
logistic迴歸
- 基本公式
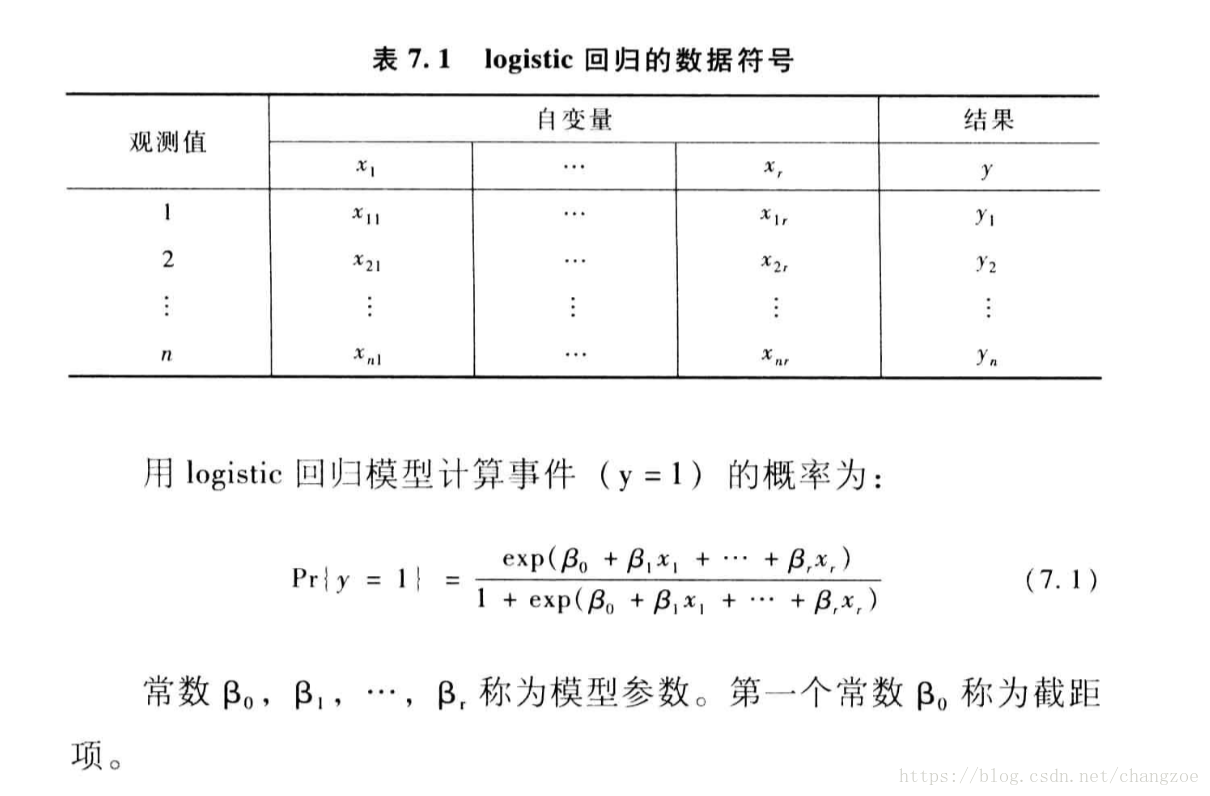

將y=1的概率記為p
- 似然方程擬合迴歸模型
資訊矩陣


模型的方差和協方差
: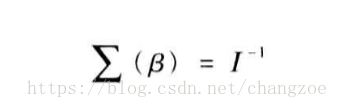
標準誤
: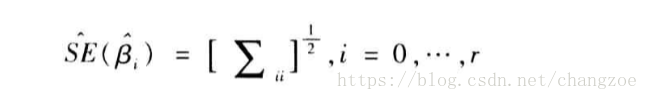
沃爾德卡方統計量:

置信區間
模型擬合的統計量
似然函式值的統計量,評估自變數引入模型的效應及aic,sc,r
hosmer-lemeshow檢驗:
全域性零假設檢驗
似然比統計量
分數統計量
沃爾德統計量能
關於概率比解讀
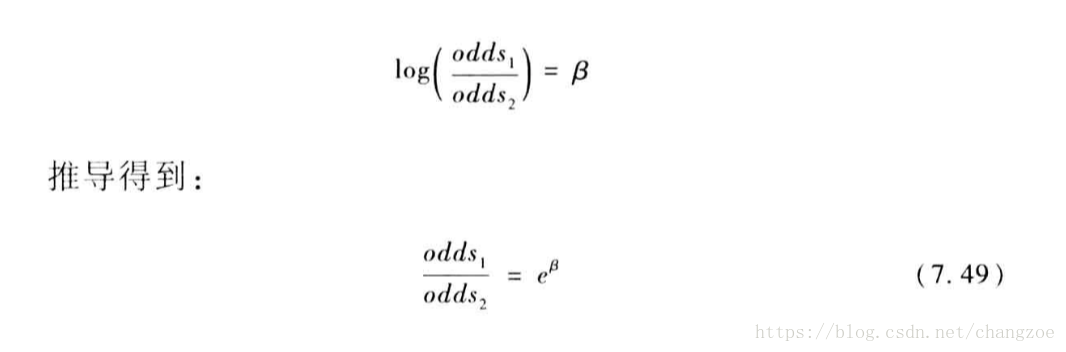
證據權重WOE
證據權重(Weight of Evidence,WOE)轉換可以將Logistic迴歸模型轉變為標準評分卡格式。引入WOE轉換的目的並不是為了提高模型質量,只是一些變數不應該被納入模型,這或者是因為它們不能增加模型值,或者是因為與其模型相關係數有關的誤差較大,其實建立標準信用評分卡也可以不採用WOE轉換。這種情況下,Logistic迴歸模型需要處理更大數量的自變數。儘管這樣會增加建模程式的複雜性,但最終得到的評分卡都是一樣的。
WOE()=ln[(違約/總違約)/(正常/總正常)]。
用WOE(x)替換變數x,
如果一個已經經過WOE轉換的自變數對logistic迴歸模型進行擬合,則該變數對應的模型引數正好是1.0
證據權重和標準評分卡
名義變數:
連續變數的WOE:
將變數分箱
若WOE值和分段好的序量表之間的線性關係或者單調關係不存在,有兩種可能的解釋:
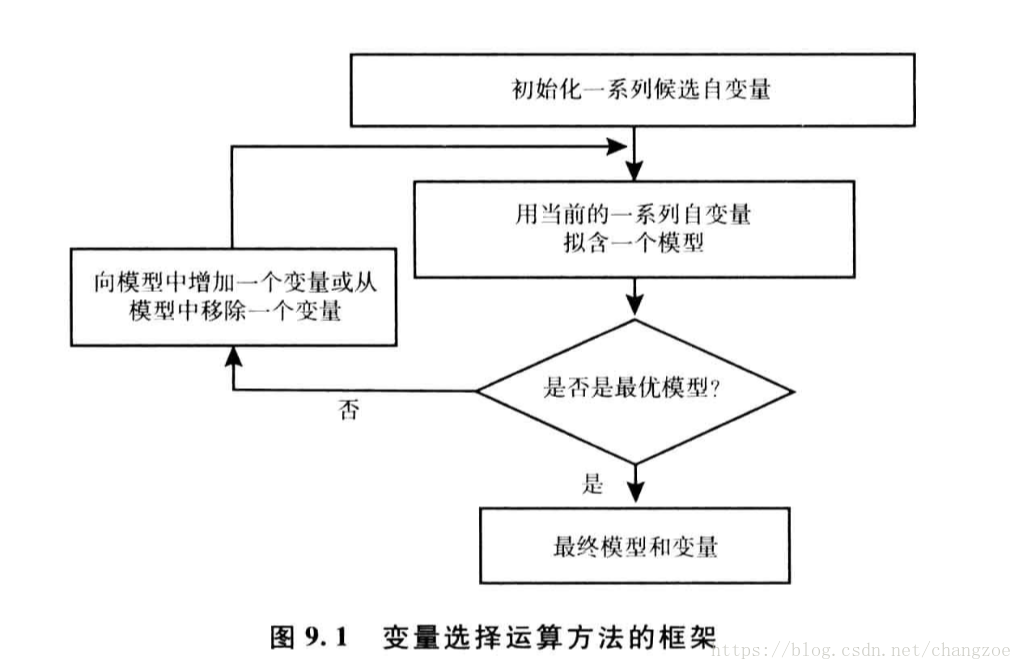
變數選擇的方法
- 使用所有變數 selection=none 將所有變數啊如模型,常用與初始探索性模型擬合
- 正向選擇 selection=forward 從幾句相對模型擬合,從沒有納入模型的變數選擇卡方統計量最大,符合條件的變數,進入的變數不會被移除
- 逆向選擇 selection=backward 移除wa l d卡方統計量的p值最大的變數
- 逐步選擇
sas引數:
逐步變數選擇
優點:
SLE = p-值 SLS= p-值
分別設定允許變數進入和保留在模型中的顯著性水平
強制變數進入模型
控制變數的優先順序順序
模型評估
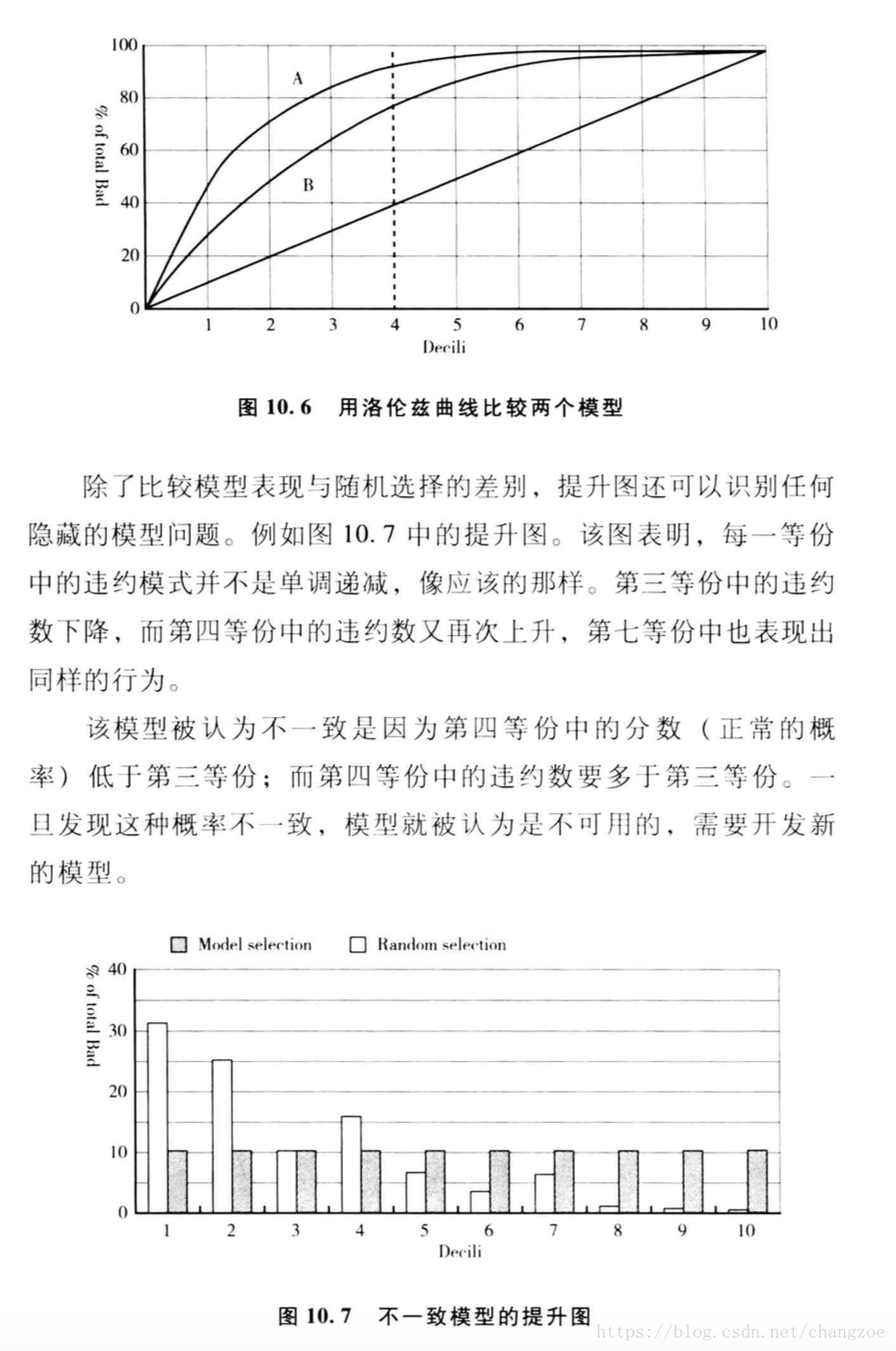
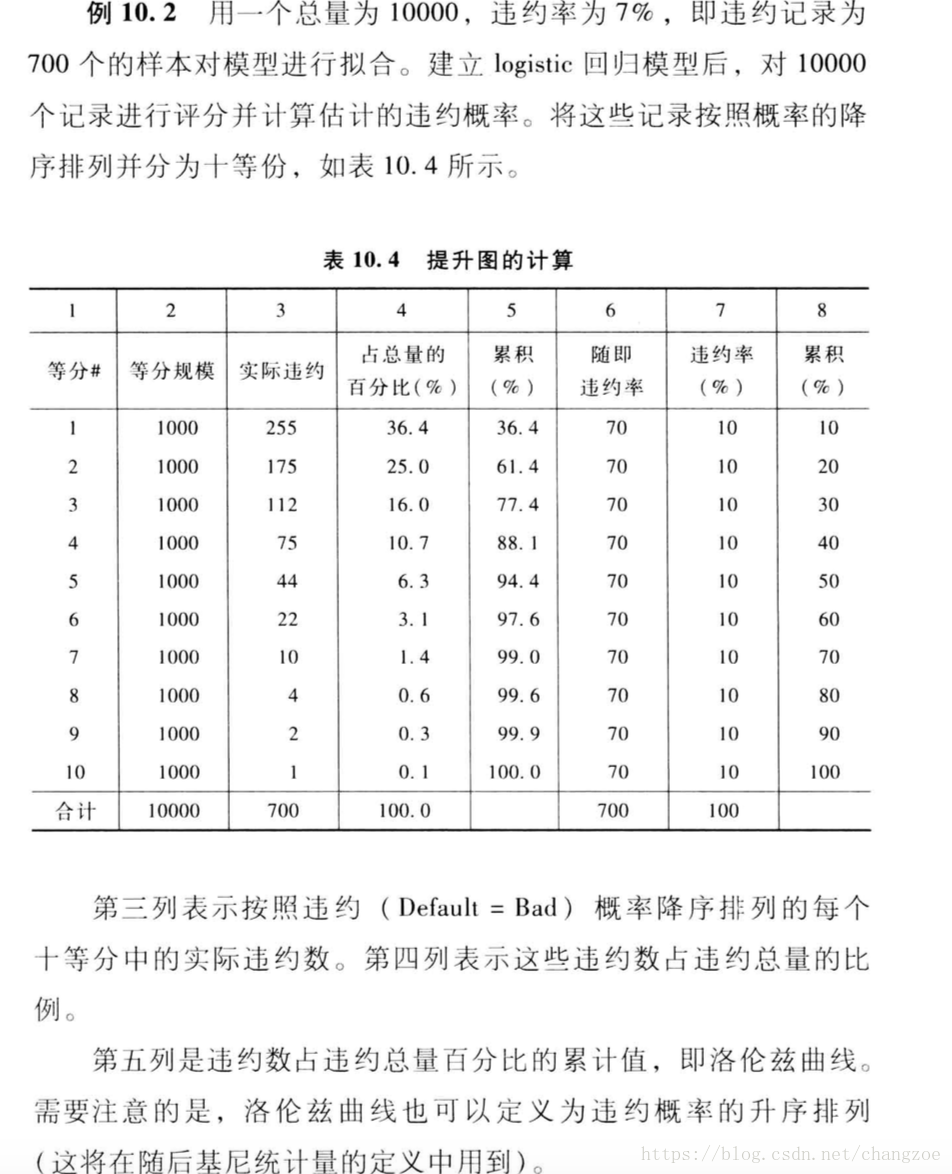
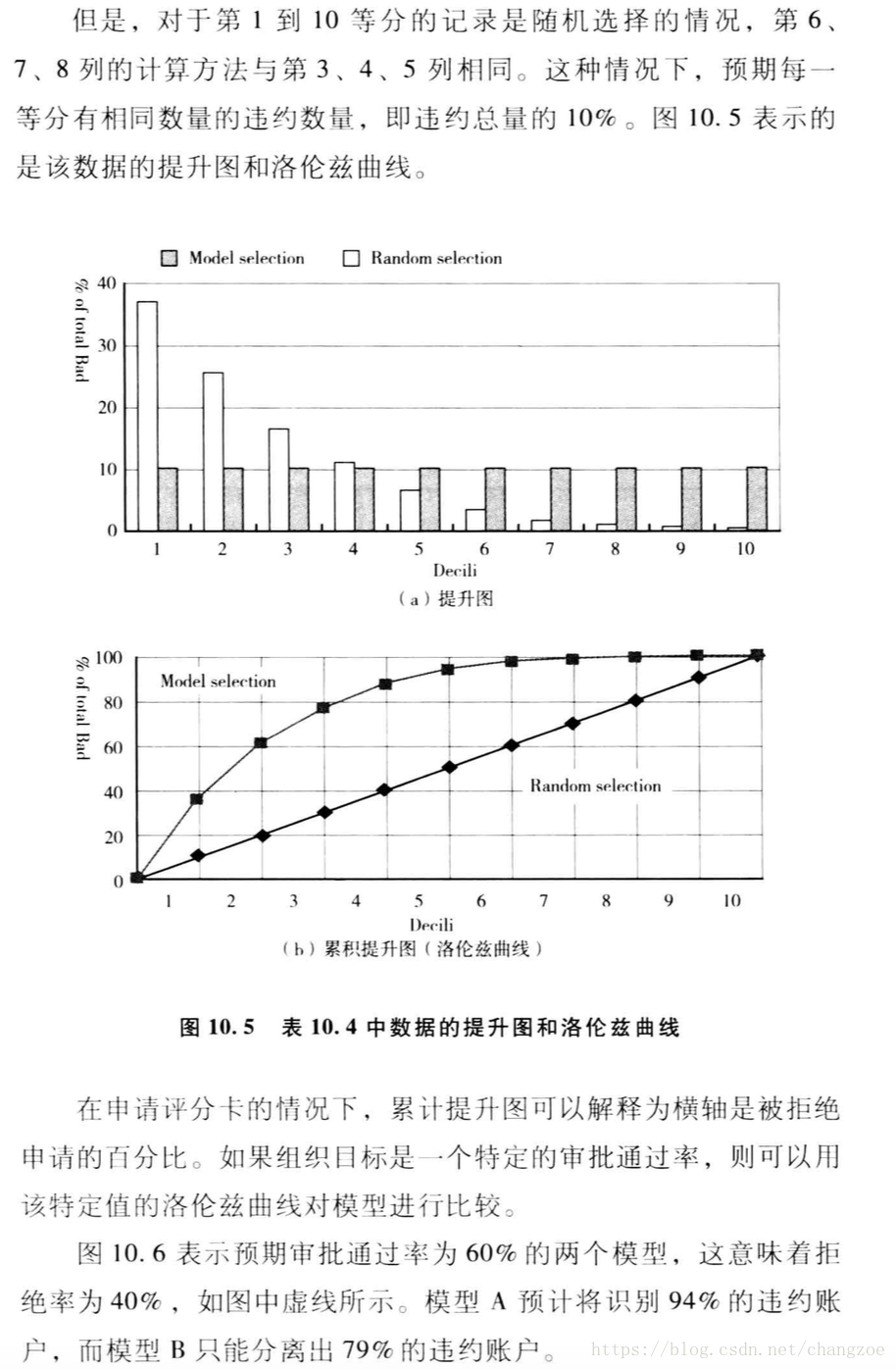
提升圖和洛倫茲曲線
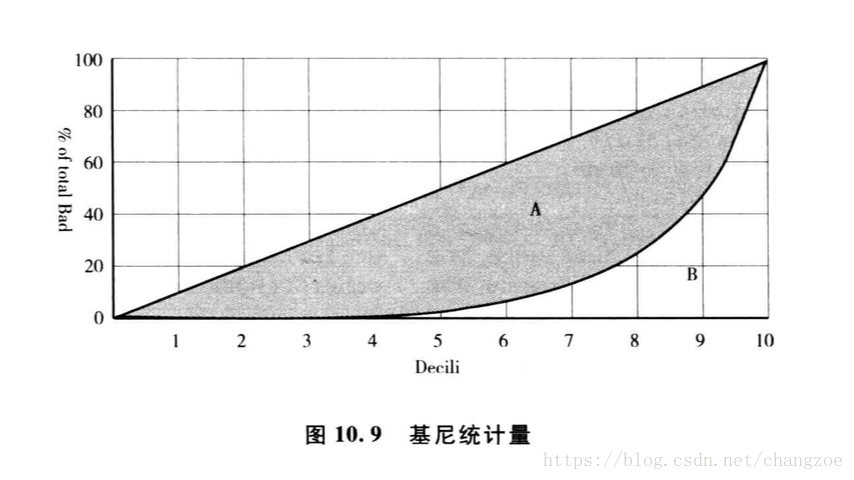
基尼係數
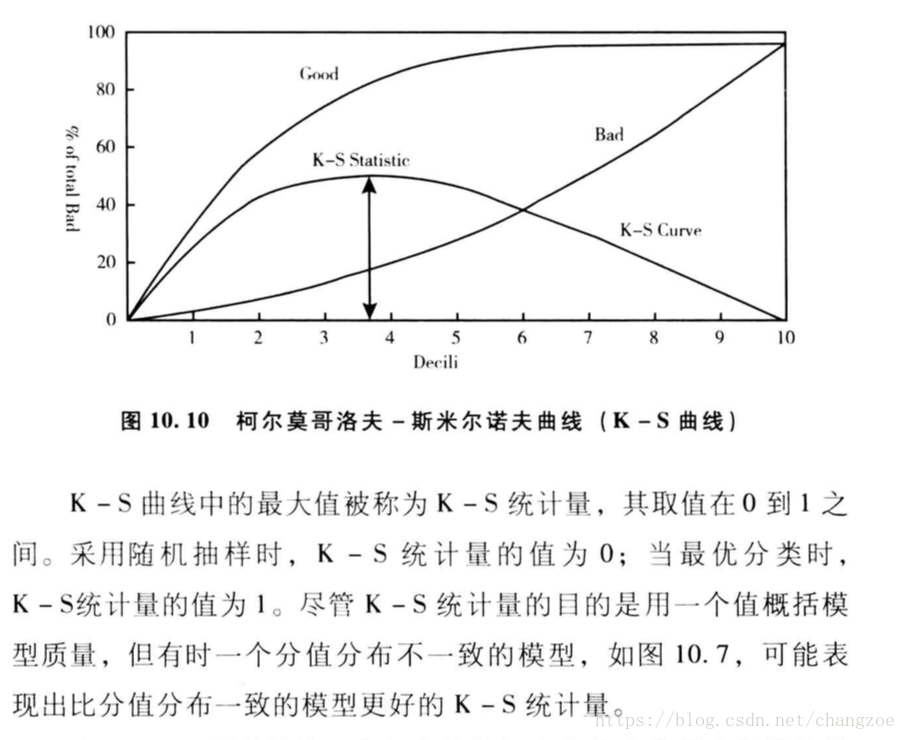
KS曲線
將總體10等分按違約概率降序排列,計算每一份違約與正常的百分比的累積分佈,繪製兩者的差異
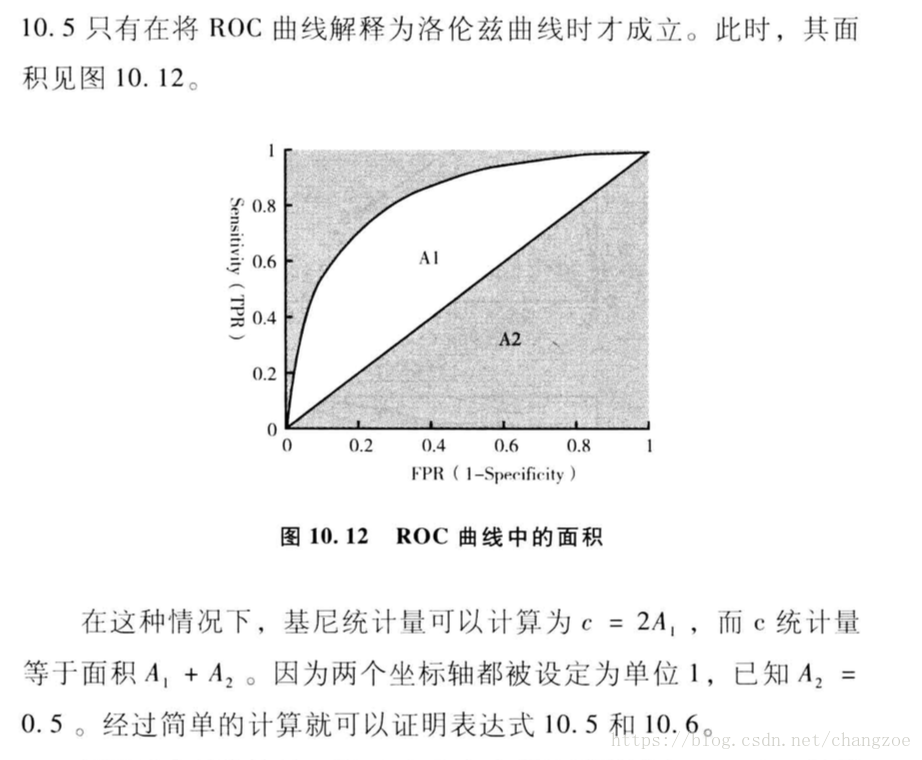
ROC曲線

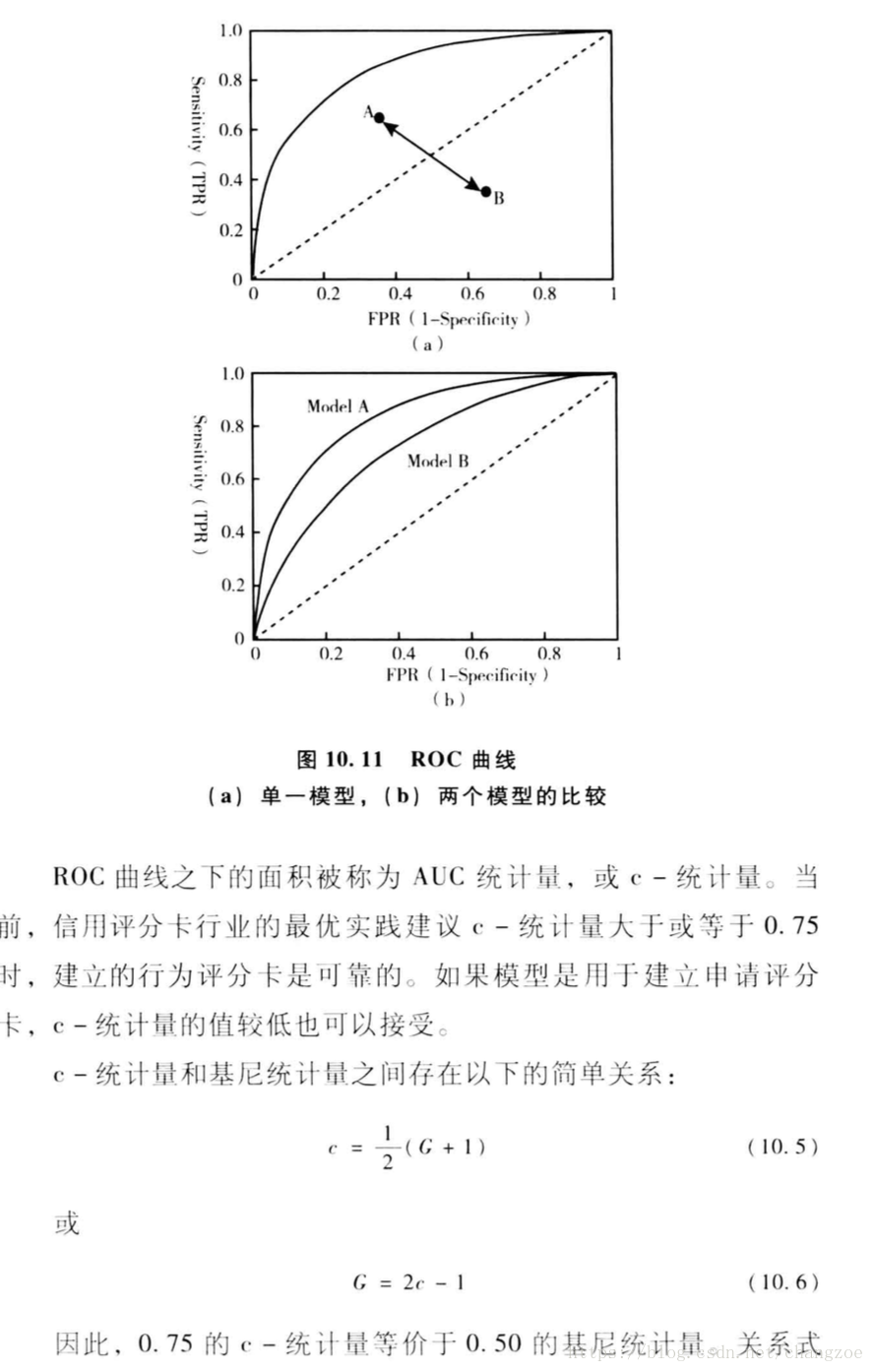
模型整體評估
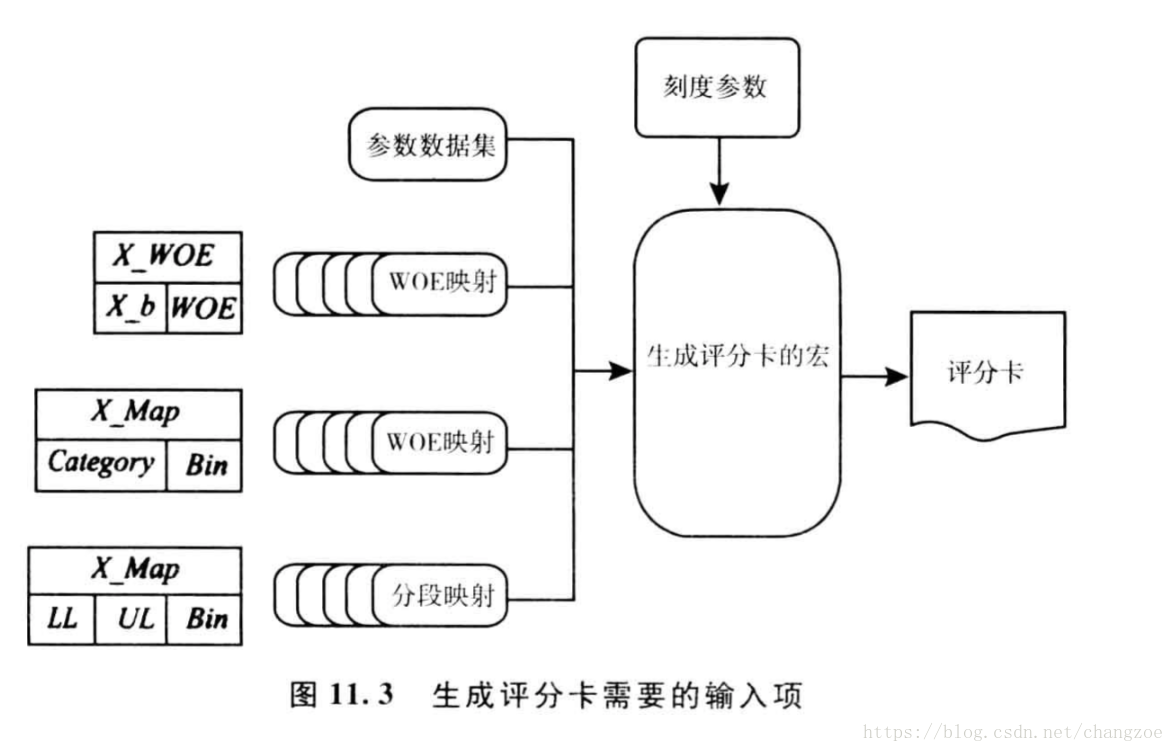
評分卡刻度與實施
評分卡的刻度
估計違約的概率為p,估計得正常的概率即為1-p,這兩個事件互斥且互為補集
違約與正常的比率:
則p為:
評分卡設定的分值刻度可以通過將分值標示為比率對數的線性表示式來定義。:
score = A - Blog(odds)
logistic 計算比率如下:
常數A和B需要兩個假設:
- 在某個特定的比率設定特定的預期分值
- 制定比率翻番的分數(pdo)
設定比率為的特定嗲的分值為,然後比率為的點的分值為,則:
解為:
A通常為稱為補償,B刻度
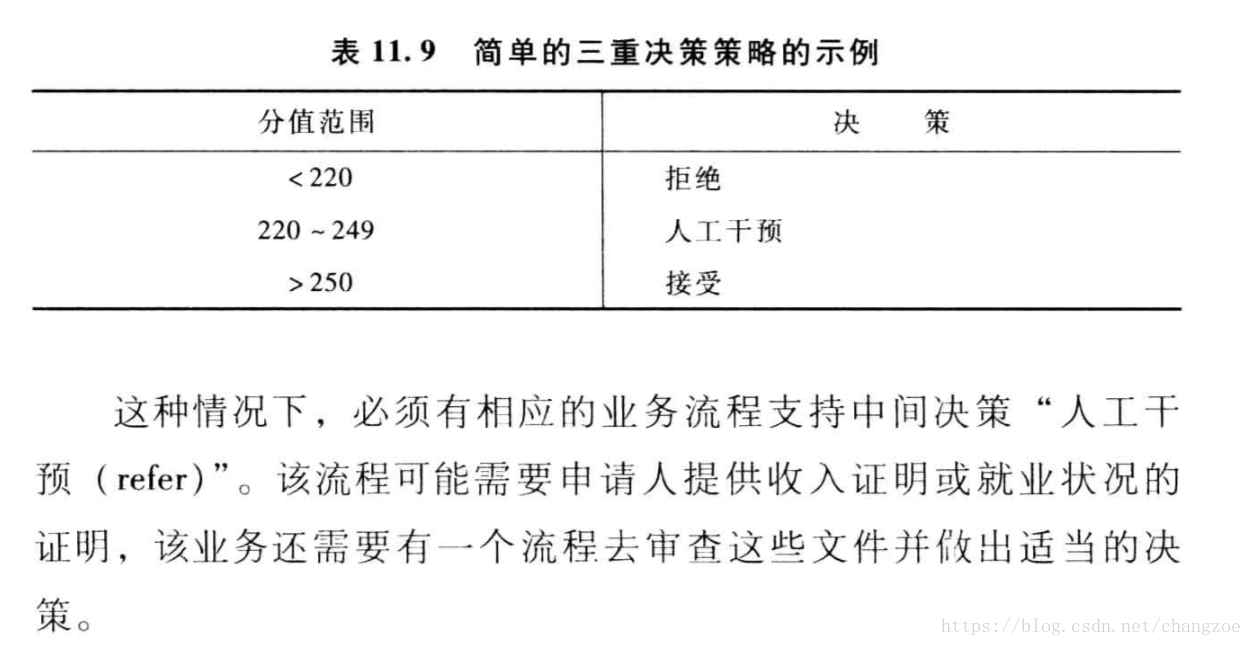
實施
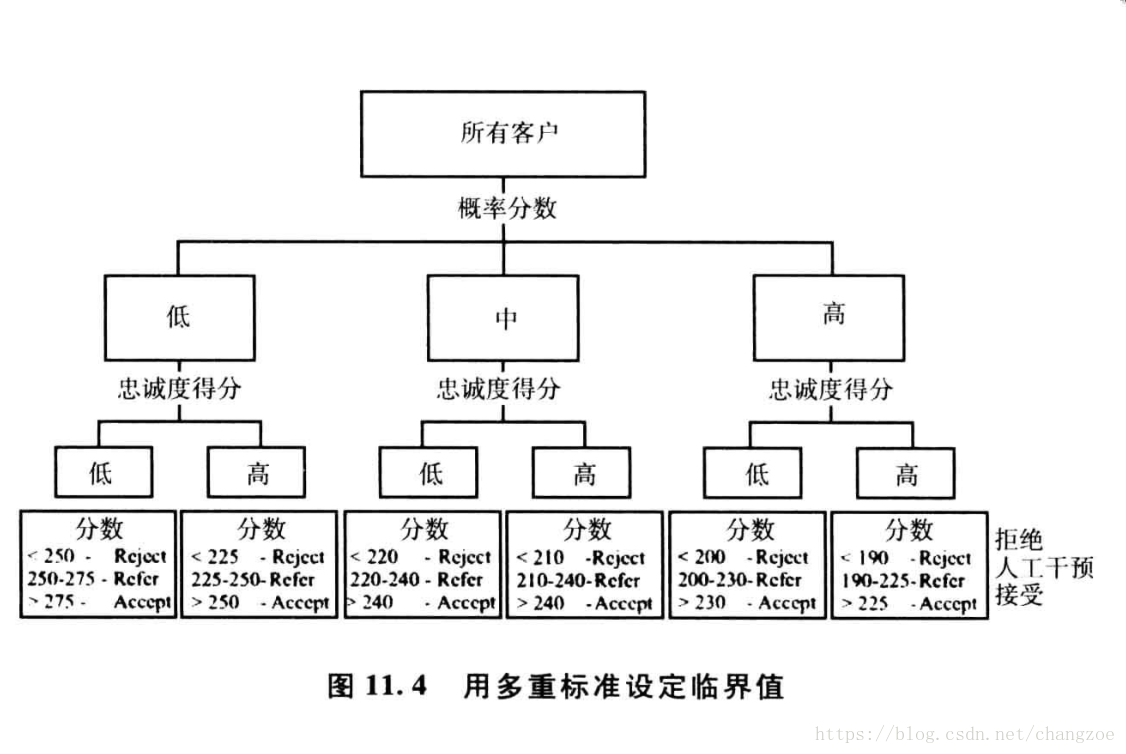
設定臨界值水平

監測報告
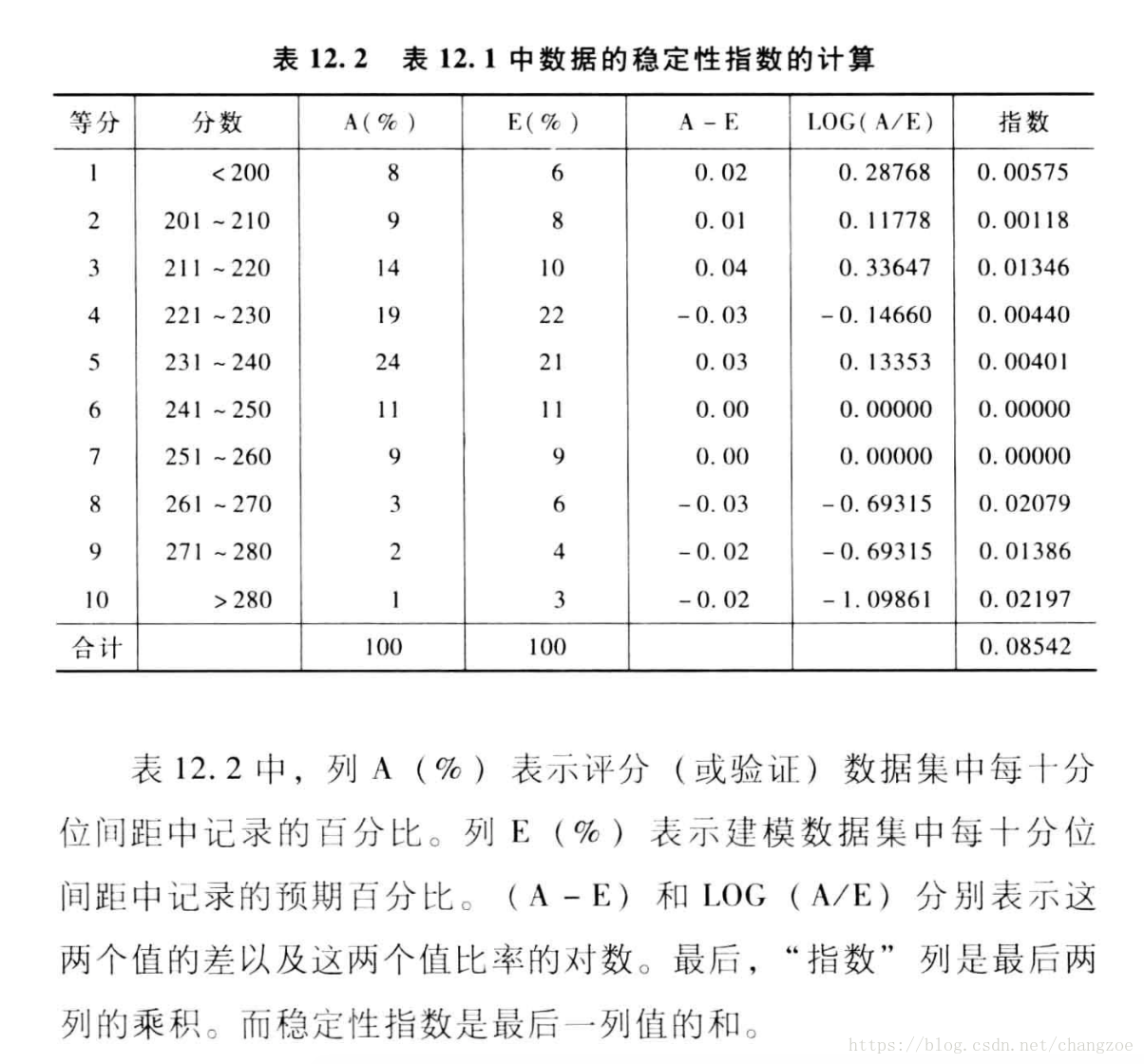
穩定性報告

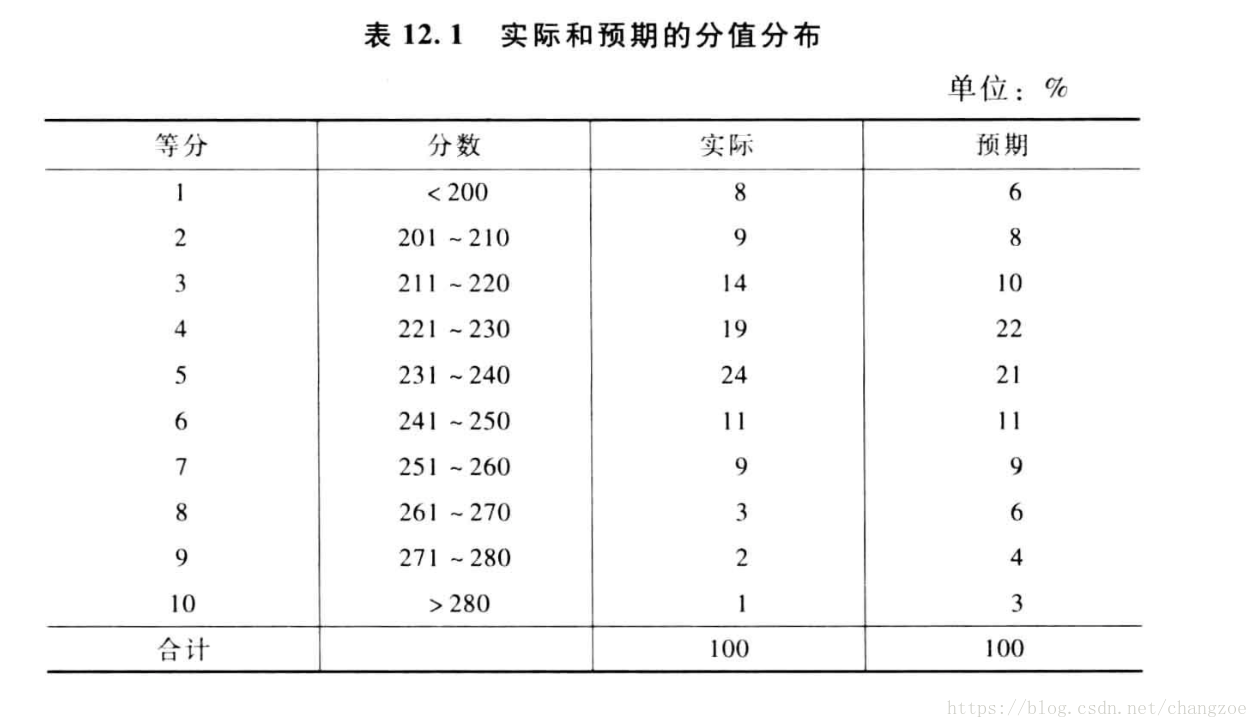
總體穩定性指數I:
與資訊值相同


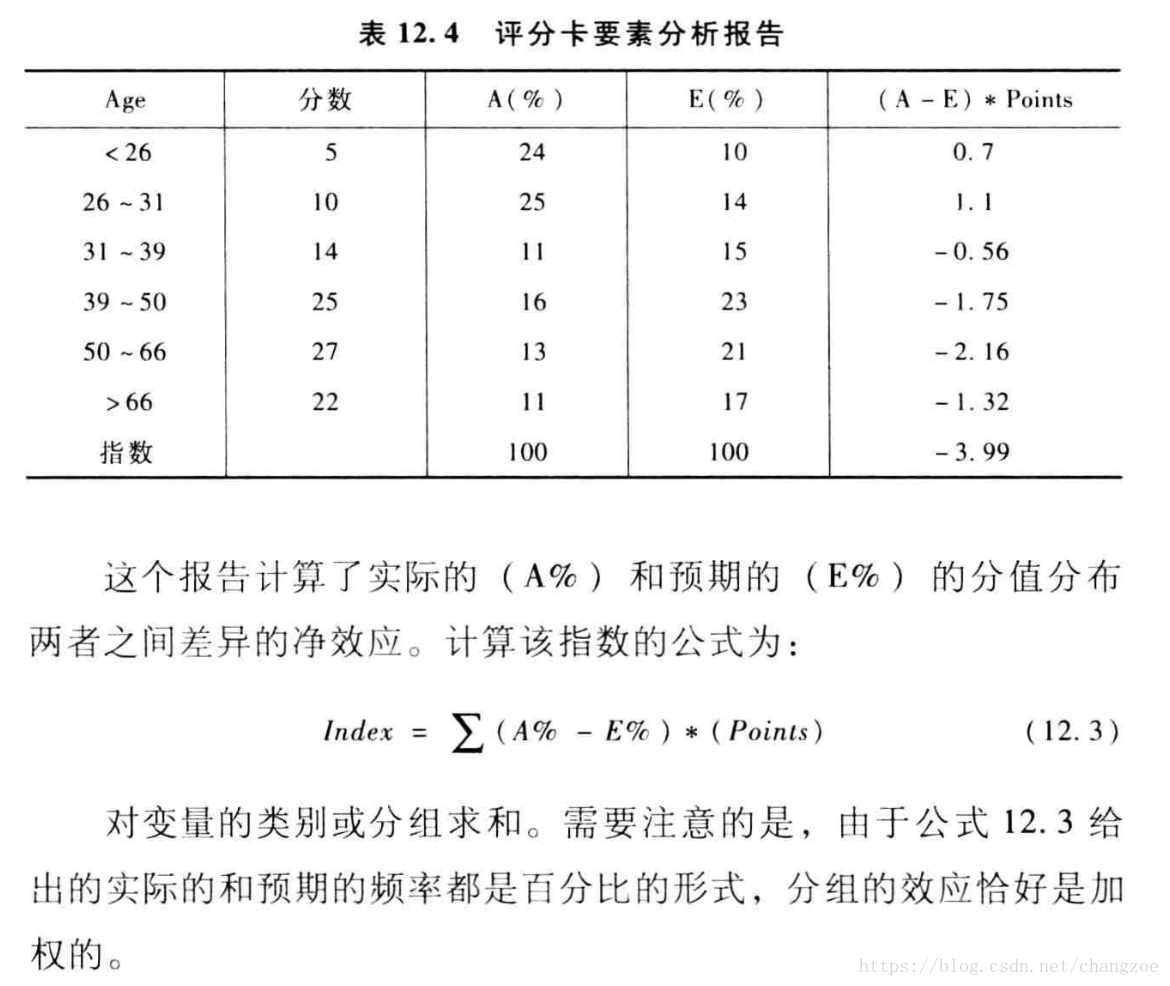
評分卡要素分析
評估自變數分佈的變化對最終評分結果的分析
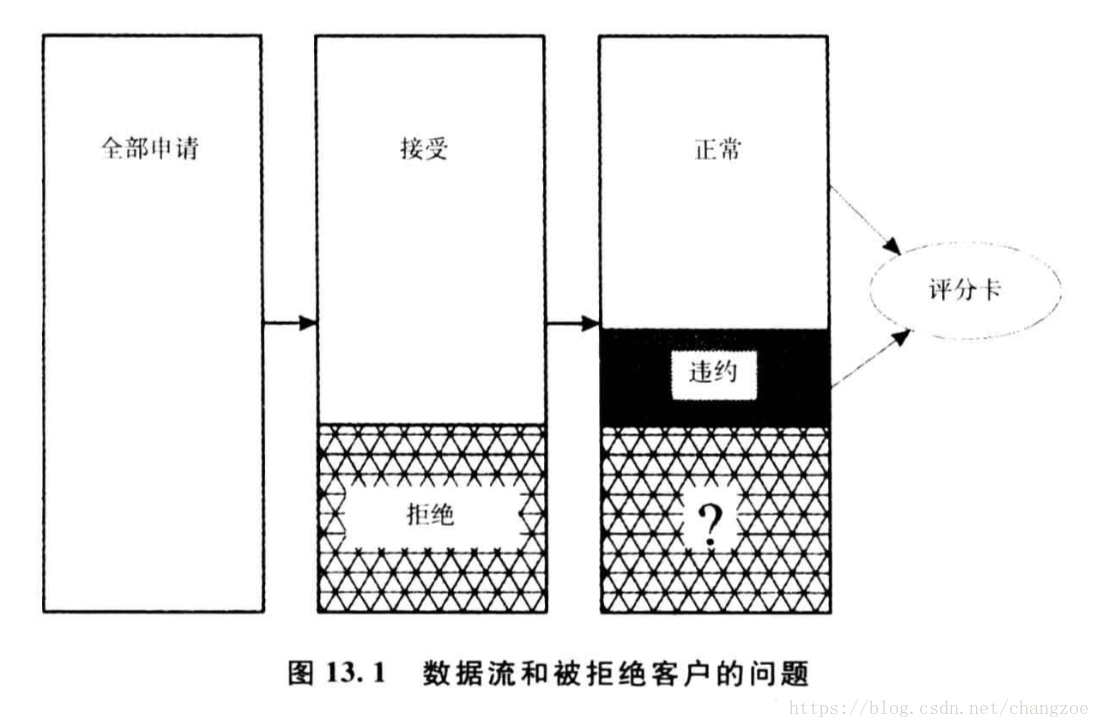
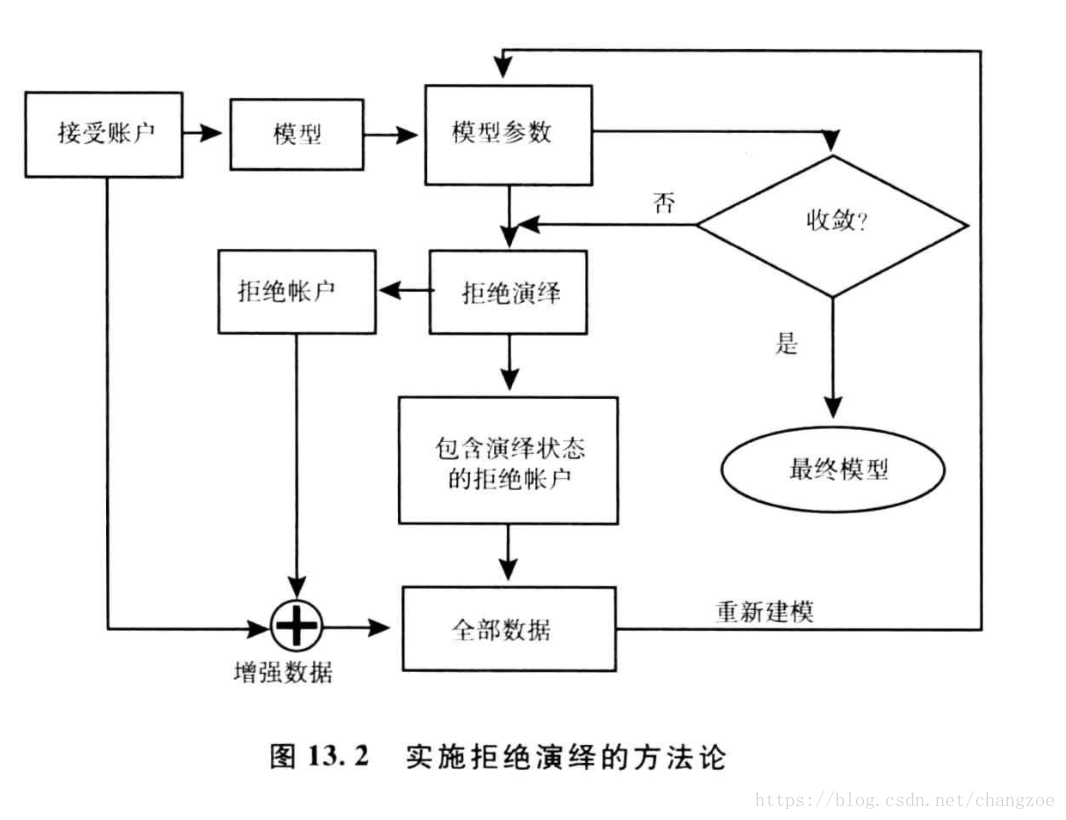
拒絕演繹
僅用於申請評分卡
建立評分卡時對被拒絕賬戶的狀態進行演繹並納入評分卡開發資料集
方法
簡單賦值法
- 忽略被拒絕申請
- 賦予所有被拒絕申請違約狀態
- 比例賦值:隨機賦予被拒絕賬戶和違約狀態
強化法
- 簡單強化:用資料中接受部分開發的模型對被拒絕賬戶進行評分,第分值的拒絕賬戶,低於預先約定的臨界值,將被賦予違約狀態,而剩餘的被拒絕賬戶則被賦予正常狀態
建議:選擇的臨界值應該使被拒絕賬戶的壞賬率是接受賬戶的2-5倍
模糊強化
打包法
引用:
信用卡評分