轉自：https://cloud.tencent.com/developer/article/1016327

定量指標是數值型的，我們還可以用迴歸的方法來篩選，那麼定性的指標怎麼辦呢？ R裡面給我們提供了非常強大的IV值計算演算法，通過引用R裡面的informationvalue包，來計算各指標的IV值，即可得到各定性指標間的重要性度量，選取其中的high predictive指標即可。 有很多小夥伴不知道informationvalue是什麼： 我大概說一下，IV值衡量兩個名義變數（其中一個是二元變數）之間關聯性的常用指標。

library(InformationValue)
library(klaR)
credit_risk<-ifelse(train_kfolddata[,"credit_risk"]=="good",0,1)
#將違約狀態變數用0和1表示，1表示違約。
tmp<-train_kfolddata[,-21]
data<-cbind(tmp,credit_risk)
data<-as.data.frame(data)

factor_vars<-c("status","credit_history","purpose","savings","employment_duration",
               "personal_status_sex","other_debtors","property",
               "other_installment_plans","housing","job","telephone","foreign_worker")
#獲取所有名義變數
all_iv<-data.frame(VARS=factor_vars,IV=numeric(length(factor_vars)),
                   STRENGTH=character(length(factor_vars)),stringsAsFactors = F)
#初始化待輸出的資料框
for(factor_var in factor_vars)
{
  all_iv[all_iv$VARS==factor_var,"IV"]<-InformationValue::IV(X=
                                                               data[,factor_var],Y=data$credit_risk)  
  #計算每個指標的IV值
  all_iv[all_iv$VARS==factor_var,"STRENGTH"]<-attr(InformationValue::IV(X=
                                                                          data[,factor_var],Y=data$credit_risk),"howgood")  
  #提取每個IV指標的描述
}
all_iv<-all_iv[order(-all_iv$IV),]    #排序IV
 

由結果可知，可選擇的定性入模指標，如表3.12所示。

綜上所述，模型開發中定量和定性的入模指標如表3.13所示。

對入模的定量和定性指標，分別進行連續變數分段（對定量指標進行分段），以便於計算定量指標的WOE和對離散變數進行必要的降維。對連續變數的分段方法通常分為等距分段和最優分段兩種方法。等距分段是指將連續變數分為等距離的若干區間，然後在分別計算每個區間的WOE值。最優分段是指根據變數的分佈屬性，並結合該變數對違約狀態變數預測能力的變化，按照一定的規則將屬性接近的數值聚在一起，形成距離不相等的若干區間，最終得到對違約狀態變數預測能力最強的最優分段。

這裡再補充一點：

轉自：https://zhuanlan.zhihu.com/p/27770760

變數選擇：

選擇上基本幾個方面，客戶物理屬性，貸前貸中貸後的表現，這裡不多敘述，比如逾期，餘額等，此處不多敘述。

實際中，在實際應用場景，很多很根據業務背景，構造特徵變數（或者稱為衍生變數），

形如

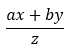
x，y和z都是變數，a和b是係數，當然還有很多形式，這方面我請教過很多人，似乎並沒有可以套用的經驗模板，只能看各位的腦洞了。

而因變數，一般選輿情90天以上的客戶標記為0（壞客戶），其他為1（好客戶）

變數篩選

這裡學校的理論都有一堆。

單變數:歸一化，離散化，缺失值處理

多變數：降維，相關係數，卡方檢驗，資訊增益。決策樹等。

這裡講一種行業經常用的基於IV值進行篩選的方式。

首先引入概念和公式。

IV的全稱是Information Value，中文意思是資訊價值，或者資訊量。

求IV值得先求woe值，這裡又引入woe的概念。

WOE的全稱是“Weight of Evidence”，即證據權重。

首先把變數分組（怎麼分後面說），然後對於每個組i，對於第i組有：

其中 是第i組壞客戶數量（bad）， 是整體壞客戶數量。同理，G就是good，好客戶的意思。

woe反映的是在自變數每個分組下違約使用者對正常使用者佔比和總體中違約使用者對正常使用者佔比之間的差異；從而可以直觀的認為woe蘊含了自變數取值對於目標變數（違約概率）的影響

而IV值得公式如下：

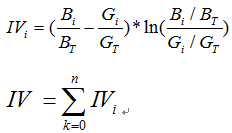
我們可以看到IV值其實是woe值加權求和。這個加權主要是消除掉各分組中數量差異帶來的誤差。

比如如果只用woe的絕對值求和，如果一些分組中，A組數量很小，B組數量很大（顯然這樣的分組不合理），這是B的woe值就很小，A組很大，求和的woe也不會小，顯然這樣不合理。比如：

最後我們可以根據每個變數VI值的大小排序去篩選變數。VI越大的越要保留。

變數處理

變數離散化：

評分卡模型用的是logistics，基本上都需要變數離散化後，效果才比較好。

離散化一般有幾種方式：合併和切割。

合併：先把變數分為N份，然後兩兩合併，看是否滿足停止合併條件。

切割：先把變數一分為二，看切割前後是否滿足某個條件，滿足則再切割。

而所謂的條件，一般有兩種，卡方檢驗，資訊增益。

傳送門：卡方檢驗 卡方檢驗-百度百科

資訊增益 百度百科-資訊增益

所以流程總結下來就是

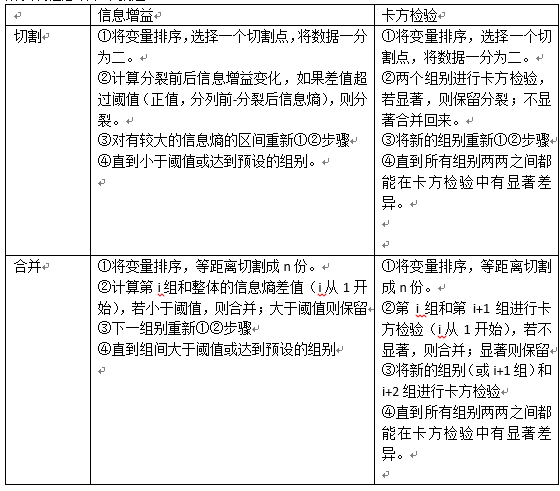
啞變數：

當一些變數是非等級的字串變數怎麼辦呢?

比如職業ABC，有的人寫成123，其實這樣就會有很大誤差，ABC3種職業本無關係，但變為123後，1 2之間和1 3之間，似乎前者更加密切，對於模型來說（2-1<3-1）。所以我們需要將其變成啞變數。形如：

N組變數用M個變數的0和1來代替(M肯定小於N),在用這些新變數擬合模型。