邊緣檢測之Canny
1. 寫在前面
最近在做邊緣檢測方面的一些工作,在網路上也找了很多有用的資料,感謝那些積極分享知識的先輩們,自己在理解Canny邊緣檢測演算法的過程中也走了一些彎路,在程式設計實現的過程中,也遇到了一個讓我懷疑人生的BUG(日了狗狗)。就此寫下此文,作為後記,也希望此篇文章可以幫助那些在理解Canny演算法的道路上暫入迷途的童鞋。廢話少說,上乾貨。
2. Canny邊緣檢測演算法的發展歷史
Canny邊緣檢測於1986年由JOHN CANNY首次在論文《A Computational Approach to Edge Detection》中提出,就此拉開了Canny邊緣檢測演算法的序幕。
Canny邊緣檢測是從不同視覺物件中提取有用的結構資訊並大大減少要處理的資料量的一種技術,目前已廣泛應用於各種計算機視覺系統。Canny發現,在不同視覺系統上對邊緣檢測的要求較為類似,因此,可以實現一種具有廣泛應用意義的邊緣檢測技術。邊緣檢測的一般標準包括:
1) 以低的錯誤率檢測邊緣,也即意味著需要儘可能準確的捕獲影象中儘可能多的邊緣。
2) 檢測到的邊緣應精確定位在真實邊緣的中心。
3) 影象中給定的邊緣應只被標記一次,並且在可能的情況下,影象的噪聲不應產生假的邊緣。
為了滿足這些要求,Canny使用了變分法。Canny檢測器中的最優函式使用四個指數項的和來描述,它可以由高斯函式的一階導數來近似。
在目前常用的邊緣檢測方法中,Canny邊緣檢測演算法是具有嚴格定義的,可以提供良好可靠檢測的方法之一。由於它具有滿足邊緣檢測的三個標準和實現過程簡單的優勢,成為邊緣檢測最流行的演算法之一。
3. Canny邊緣檢測演算法的處理流程
Canny邊緣檢測演算法可以分為以下5個步驟:
1) 使用高斯濾波器,以平滑影象,濾除噪聲。
2) 計算影象中每個畫素點的梯度強度和方向。
3) 應用非極大值(Non-Maximum Suppression)抑制,以消除邊緣檢測帶來的雜散響應。
4) 應用雙閾值(Double-Threshold)檢測來確定真實的和潛在的邊緣。
5) 通過抑制孤立的弱邊緣最終完成邊緣檢測。
下面詳細介紹每一步的實現思路。
3.1 高斯平滑濾波
為了儘可能減少噪聲對邊緣檢測結果的影響,所以必須濾除噪聲以防止由噪聲引起的錯誤檢測。為了平滑影象,使用高斯濾波器與影象進行卷積,該步驟將平滑影象,以減少邊緣檢測器上明顯的噪聲影響。大小為(2k+1)x(2k+1)的高斯濾波器核的生成方程式由下式給出:
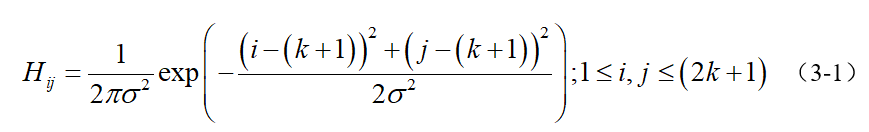
下面是一個sigma = 1.4,尺寸為3x3的高斯卷積核的例子(需要注意歸一化):

若影象中一個3x3的視窗為A,要濾波的畫素點為e,則經過高斯濾波之後,畫素點e的亮度值為:

其中*為卷積符號,sum表示矩陣中所有元素相加求和。
重要的是需要理解,高斯卷積核大小的選擇將影響Canny檢測器的效能。尺寸越大,檢測器對噪聲的敏感度越低,但是邊緣檢測的定位誤差也將略有增加。一般5x5是一個比較不錯的trade off。
3.2 計算梯度強度和方向
影象中的邊緣可以指向各個方向,因此Canny演算法使用四個運算元來檢測影象中的水平、垂直和對角邊緣。邊緣檢測的運算元(如Roberts,Prewitt,Sobel等)返回水平Gx和垂直Gy方向的一階導數值,由此便可以確定畫素點的梯度G和方向theta 。

其中G為梯度強度, theta表示梯度方向,arctan為反正切函式。下面以Sobel運算元為例講述如何計算梯度強度和方向。
x和y方向的Sobel運算元分別為:
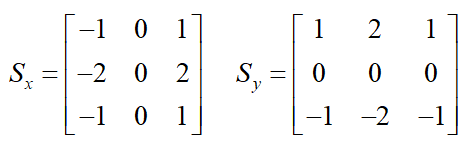
其中Sx表示x方向的Sobel運算元,用於檢測y方向的邊緣; Sy表示y方向的Sobel運算元,用於檢測x方向的邊緣(邊緣方向和梯度方向垂直)。在直角座標系中,Sobel運算元的方向如下圖所示。
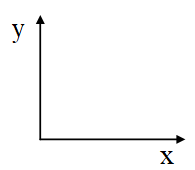
圖3-1 Sobel運算元的方向
若影象中一個3x3的視窗為A,要計算梯度的畫素點為e,則和Sobel運算元進行卷積之後,畫素點e在x和y方向的梯度值分別為:

其中*為卷積符號,sum表示矩陣中所有元素相加求和。根據公式(3-2)便可以計算出畫素點e的梯度和方向。
3.3 非極大值抑制
非極大值抑制是一種邊緣稀疏技術,非極大值抑制的作用在於“瘦”邊。對影象進行梯度計算後,僅僅基於梯度值提取的邊緣仍然很模糊。對於標準3,對邊緣有且應當只有一個準確的響應。而非極大值抑制則可以幫助將區域性最大值之外的所有梯度值抑制為0,對梯度影象中每個畫素進行非極大值抑制的演算法是:
1) 將當前畫素的梯度強度與沿正負梯度方向上的兩個畫素進行比較。
2) 如果當前畫素的梯度強度與另外兩個畫素相比最大,則該畫素點保留為邊緣點,否則該畫素點將被抑制。
通常為了更加精確的計算,在跨越梯度方向的兩個相鄰畫素之間使用線性插值來得到要比較的畫素梯度,現舉例如下:
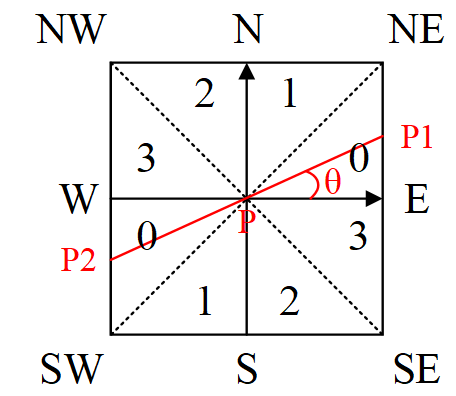
圖3-2 梯度方向分割
如圖3-2所示,將梯度分為8個方向,分別為E、NE、N、NW、W、SW、S、SE,其中0代表00~45o,1代表450~90o,2代表-900~-45o,3代表-450~0o。畫素點P的梯度方向為theta,則畫素點P1和P2的梯度線性插值為:
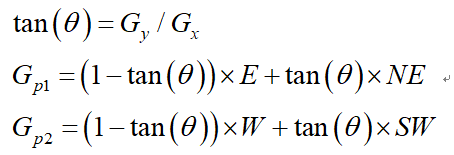
因此非極大值抑制的虛擬碼描寫如下:
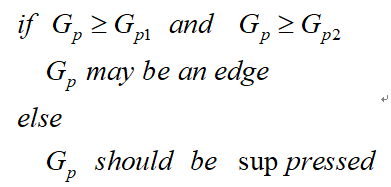
需要注意的是,如何標誌方向並不重要,重要的是梯度方向的計算要和梯度運算元的選取保持一致。
3.4 雙閾值檢測
在施加非極大值抑制之後,剩餘的畫素可以更準確地表示影象中的實際邊緣。然而,仍然存在由於噪聲和顏色變化引起的一些邊緣畫素。為了解決這些雜散響應,必須用弱梯度值過濾邊緣畫素,並保留具有高梯度值的邊緣畫素,可以通過選擇高低閾值來實現。如果邊緣畫素的梯度值高於高閾值,則將其標記為強邊緣畫素;如果邊緣畫素的梯度值小於高閾值並且大於低閾值,則將其標記為弱邊緣畫素;如果邊緣畫素的梯度值小於低閾值,則會被抑制。閾值的選擇取決於給定輸入影象的內容。
雙閾值檢測的虛擬碼描寫如下:
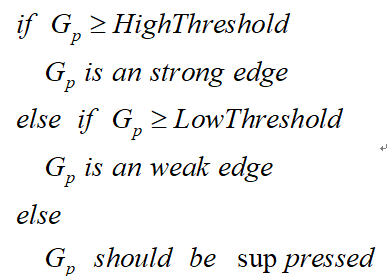
3.5 抑制孤立低閾值點
到目前為止,被劃分為強邊緣的畫素點已經被確定為邊緣,因為它們是從影象中的真實邊緣中提取出來的。然而,對於弱邊緣畫素,將會有一些爭論,因為這些畫素可以從真實邊緣提取也可以是因噪聲或顏色變化引起的。為了獲得準確的結果,應該抑制由後者引起的弱邊緣。通常,由真實邊緣引起的弱邊緣畫素將連線到強邊緣畫素,而噪聲響應未連線。為了跟蹤邊緣連線,通過檢視弱邊緣畫素及其8個鄰域畫素,只要其中一個為強邊緣畫素,則該弱邊緣點就可以保留為真實的邊緣。
抑制孤立邊緣點的虛擬碼描述如下:

4 總結
通過以上5個步驟即可完成基於Canny演算法的邊緣提取,圖5-1是該演算法的檢測效果圖,希望對大家有所幫助。

圖5-1 Canny邊緣檢測效果
附錄是完整的MATLAB原始碼,可以直接拿來執行。
附錄1
?
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 |
% -------------------------------------------------------------------------
% Edge Detection Using Canny Algorithm.
% Auther: Yongli Yan.
% Mail: [email protected]
% Date: 2017.08.01.
% The direction of Sobel operator.
% ^(y)
% |
% |
% |
% 0--------->(x)
% Direction of Gradient:
% 3 2 1
% 0 P 0
% 1 2 3
% P = Current Point.
% NW N NE
% W P E
% SW S SE
% Point Index:
% f(x-1,y-1) f(x-1,y) f(x-1,y+1)
% f(x, y-1) f(x, y) f(x, y+1)
% f(x+1,y-1) f(x+1,y) f(x+1,y+1)
% Parameters:
% percentOfPixelsNotEdges: Used for selecting thresholds.
% thresholdRatio: Low thresh is this fraction of the high.
% -------------------------------------------------------------------------
function
imgCanny = edge_canny(I,gaussDim,sigma,percentOfPixelsNotEdges,thresholdRatio)
%% Gaussian smoothing filter.
m = gaussDim(1);
n = gaussDim(2);
if
mod
(m,2) == 0 ||
mod
(n,2) == 0
error
(
'The dimensionality of Gaussian must be odd!'
);
end
% Generate gaussian convolution kernel.
gaussKernel = fspecial(
'gaussian'
, [m,n], sigma);
% Image edge copy.
[m,n] =
size
(gaussKernel);
[row,col,dim] =
size
(I);
if
dim > 1
imgGray = rgb2gray(I);
else
imgGray = I;
end
imgCopy = imgReplicate(imgGray,(m-1)/2,(n-1)/2);
% Gaussian smoothing filter.
imgData =
zeros
(row,col);
for
ii = 1:row
for
jj = 1:col
window = imgCopy(ii:ii+m-1,jj:jj+n-1);
GSF = window.*gaussKernel;
imgData(ii,jj) =
sum
(GSF(:));
end
end
%% Calculate the gradient values for each pixel.
% Sobel operator.
dgau2Dx = [-1 0 1;-2 0 2;-1 0 1];
dgau2Dy = [1 2 1;0 0 0;-1 -2 -1];
[m,n] =
size
(dgau2Dx);
% Image edge copy.
imgCopy = imgReplicate(imgData,(m-1)/2,(n-1)/2);
% To store the gradient and direction information.
gradx =
zeros
(row,col);
grady =
zeros
(row,col);
gradm =
zeros
(row,col);
dir
=
zeros
(row,col);
% Direction of gradient.
% Calculate the gradient values for each pixel.
for
ii = 1:row
for
jj = 1:col
window = imgCopy(ii:ii+m-1,jj:jj+n-1);
dx = window.*dgau2Dx;
dy = window.*dgau2Dy;
dx = dx';
% Make the sum more accurate.
dx =
sum
(dx(:));
dy =
sum
(dy(:));
gradx(ii,jj) = dx;
grady(ii,jj) = dy;
gradm(ii,jj) =
sqrt
(dx^2 + dy^2);
% Calculate the angle of the gradient.
theta =
atand
(dy/dx) + 90;
% 0~180.
% Determine the direction of the gradient.
if
(theta >= 0 && theta < 45)
dir
(ii,jj) = 2;
elseif
(theta >= 45 && theta < 90)
dir
(ii,jj) = 3;
elseif
(theta >= 90 && theta < 135)
dir
(ii,jj) = 0;
else
dir
(ii,jj) = 1;
end
end
end
% Normalize for threshold selection.
magMax =
max
(gradm(:));
if
magMax ~= 0
gradm = gradm / magMax;
end
%% Plot 3D gradient graph.
% [xx, yy] = meshgrid(1:col, 1:row);
% figure;
% surf(xx,yy,gradm);
%% Threshold selection.
counts = imhist(gradm, 64);
highThresh =
find
(
cumsum
(counts) > percentOfPixelsNotEdges*row*col,1,
'first'
) / 64;
lowThresh = thresholdRatio*highThresh;
%% Non-Maxima Suppression(NMS) Using Linear Interpolation.
gradmCopy =
zeros
(row,col);
imgBW =
zeros
(row,col);
for
ii = 2:row-1
for
jj = 2:col-1
E = gradm(ii,jj+1);
S = gradm(ii+1,jj);
W = gradm(ii,jj-1);
N = gradm(ii-1,jj);
NE = gradm(ii-1,jj+1);
NW = gradm(ii-1,jj-1);
SW = gradm(ii+1,jj-1);
SE = gradm(ii+1,jj+1);
% Linear interpolation.
% dy/dx = tan(theta).
% dx/dy = tan(90-theta).
gradValue = gradm(ii,jj);
if
dir
(ii,jj) == 0
d =
abs
(grady(ii,jj)/gradx(ii,jj));
gradm1 = E*(1-d) + NE*d;
gradm2 = W*(1-d) + SW*d;
elseif
dir
(ii,jj) == 1
d =
abs
(gradx(ii,jj)/grady(ii,jj));
gradm1 = N*(1-d) + NE*d;
gradm2 = S*(1-d) + SW*d;
elseif
dir
(ii,jj) == 2
d =
abs
(gradx(ii,jj)/grady(ii,jj));
gradm1 = N*(1-d) + NW*d;
gradm2 = S*(1-d) + SE*d;
elseif
dir
(ii,jj) == 3
d =
abs
(grady(ii,jj)/gradx(ii,jj));
gradm1 = W*(1-d) + NW*d;
gradm2 = E*(1-d) + SE*d;
else
gradm1 = highThresh;
gradm2 = highThresh;
end
% Non-Maxima Suppression.
if
gradValue >= gradm1 && gradValue >= gradm2
if
gradValue >= highThresh
imgBW(ii,jj) = 1;
gradmCopy(ii,jj) = highThresh;
elseif
gradValue >= lowThresh
gradmCopy(ii,jj) = lowThresh;
else
gradmCopy(ii,jj) = 0;
end
else
gradmCopy(ii,jj) = 0;
end
end
end
%% High-Low threshold detection.Double-Threshold.
|
