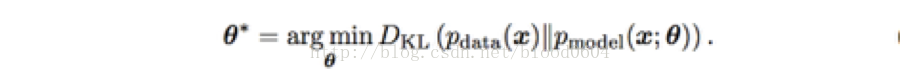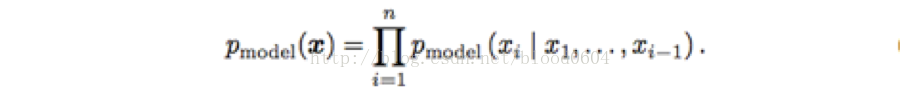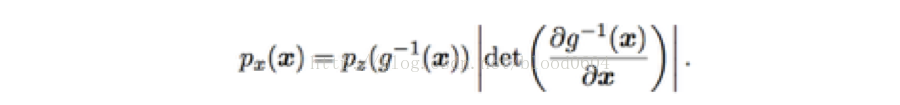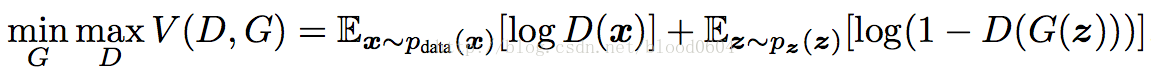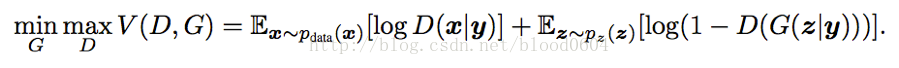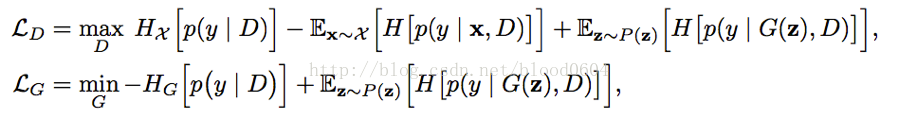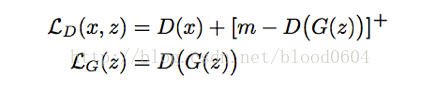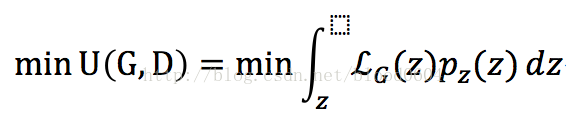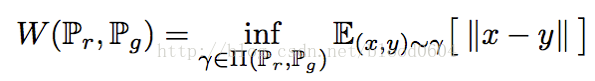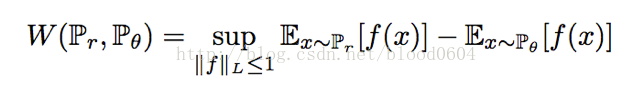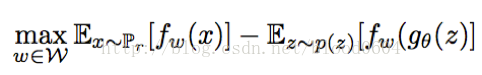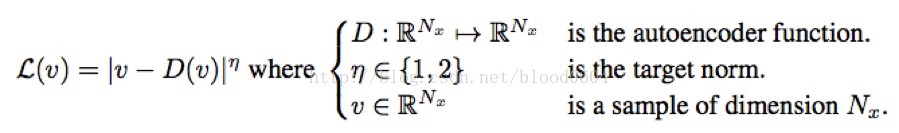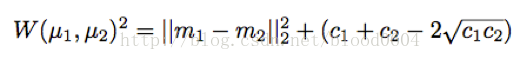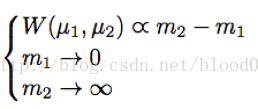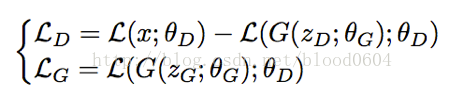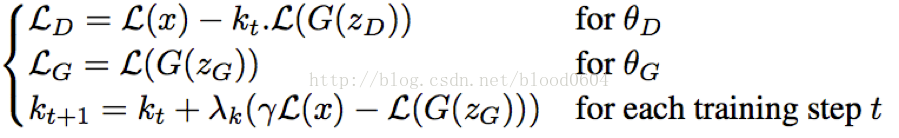生成對抗網路(GAN)的理論與應用完整入門介紹
文章來源:https://blog.csdn.net/blood0604/article/details/73635586?locationNum=1&fps=1
本文包含以下內容:
1.為什麼生成模型值得研究
2.生成模型的分類
3.GAN相對於其他生成模型相比有什麼優勢
4.GAN基本模型
5.改進的GANs
6.GAN有哪些應用
7.GAN的前沿研究
一、為什麼生成模型值得研究
主要基於以下幾個原因:
1. 從生成模型中訓練和取樣資料能很好的測試我們表示和操作高維概率分佈的能力。而這種能力在數學和工程方面都有廣泛的應用。
2. 生成模型可以通過很多方式應用到強化學習中。強化學習演算法一般分為兩類:基於模型的(包含生成模型)和與模型無關的。時間序列生成模型可以模擬將來的很多種可能。比如,可以學習一個條件概率分佈模型,把當前時刻的狀態和假設的動作作為輸入,用生成模型來產生未來的狀態。通過輸入可能的動作,生成並預測。另一種結合強化學習的方式是生成假想的環境進行測試,這樣可以不用在真實環境下測試,從而造成損失。
3. 生成模型還可以填補缺失資訊。特別是在半監督學習中的應用,由於真實環境下,很少有帶標註的資訊,而且標註資訊往往依靠高成本的人工標註。生成模型,特別是GANs,能夠在很少標註樣本的情況下,提高半監督學習演算法的泛化能力。同時,給定一張二維圖片,可以通過生成模型來填補更多的影象資訊,生成可能的三維影象。
4. 生成模型,可以使機器學習利用混合多模型進行輸出。對於很多工而言,對一個輸入而言,可對映到多個正確輸出。很多傳統的機器學演算法,如最小化均方誤差演算法,無法訓練模型來產生多個正確的輸出。比如預測視訊的下一幀。
5. 最後,很多工本質上是需要從多種分佈中產生真實的樣本。如單張圖片的超解析度任務,需要給低解析度的影象填補缺失資訊合成高解析度影象。相對於GAN,其他生成模型往往對多種可能的生成影象進行平均,從在造成影象模糊。而GAN,則會生成多個可能的清晰影象,從而增加了其多樣性——雖然GAN也存在模式塌陷(modecollapse)問題,即多個輸入對映到一個輸出上。最新的一些研究可以利用GANs,通過使用者想象的粗略描述來生成相關的真實圖片。影象到影象的“翻譯”,可以把框架圖或素描來轉換成真實的圖片——雖然這個任務的難度比較大,還是很有前景的,值得去探索的。
二、生成模型
1. 最大似然估計。通過一個帶有引數的模型來估計概率分佈,並在訓練資料上選擇使似然函式(一般的使用log函式)最大化的引數。GAN基本模型中,最大化似然函式等價於最小化KL散度——用來度量兩個概率之間的“距離”。
2. 深度生成模型的分類:引數的概率分佈、非引數的概率分佈
FVBN、GAN、VAE這三種是目前最流行的生成模型方法。
1) 引數的概率密度函式模型(即預先假設服從某種分佈)
i. 全視覺化置信網路:
採用概率的鏈式規則分解概率分佈,將n維向量的輸入分解為一維的概率分佈。缺點是,必須依順序生成樣本(先x1,然後x2...),不能並行化計算,也沒法進行互動,計算耗時(如,需要兩分鐘的計算才能生成一秒的語音資料)。
ii. 非線性獨立成分分析:
假設存在一個連續、可導、可逆的函式g,將隱變數z對映到樣本空間x,那麼x的概率分佈與z的概率分佈就建立了如下聯絡
該方法的主要缺點是,函式g需要精確地設計,以滿足連續、可導、可逆的要求。同時,可逆也要求隱變數z與x有相同的維數。而GAN對函式g的限制很少,也不要求x與z有相同的維數。FVBN、VAE等模型簇的優點是,由於概率密度是清晰表述的,從而利用最大似然估計進行計算也很高效。也有一些模型利用清晰表述的概率密度函式,但是需要近似(採用變分方法的判別式近似,採用馬爾科夫鏈-蒙特卡洛方法的隨機近似)。變分方法近似用一個函式L逼近log似然函式的下确界,由於兩個函式之間總是存在間隙或無法完美逼近,同時,也沒有一個好的方法來評估影象的質量,因此,變分方法(如VAE)產生的圖片比較模糊。馬爾科夫鏈通過不斷重複x’~q(x’|x)這個過程來生成樣本,最終收斂到模型中樣本。但收斂過程比較慢,也不確定何時收斂。玻爾茲曼機往往採用這種方法進行生成樣本,由於其基於馬爾科夫鏈技術,且沒法擴充套件到像ImageNet圖片生成這種問題中,現在來說,玻爾茲曼機的應用相對較少。
2)非引數的概率密度函式模型
i. 生成隨機網路:
基於真實資料模型的取樣,由於也採用馬爾科夫鏈轉換操作,因此,很難擴充套件到高維資料,並且計算成本比較高。
ii. 生成對抗網路
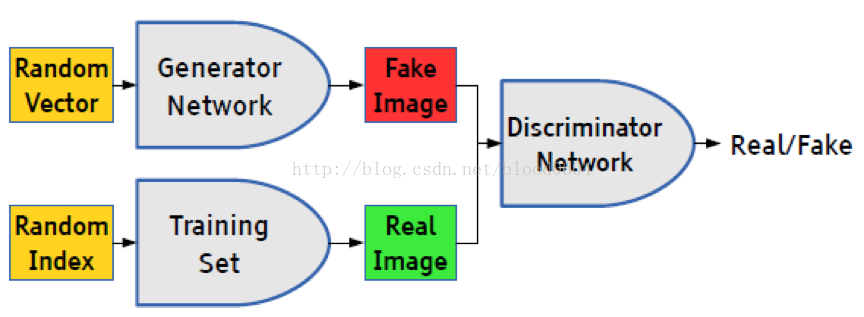
基於極小極大博弈而設計的對抗網路框架,包括生成器和判別器。生成器(如採用MLP網路表示生成函式)可以生成偽造的樣本,與真實樣本同時輸入判別器(如採用MLP網路),判別器根據偽造樣本(g(z),0)和真實樣本(x,1)最大化判別真假的概率。生成器最大化判別器無法判別的概率,即最小化偽造樣本的概率分佈與真實資料的概率分佈之間的“距離”。
生成器G可以用深度神經網路來表示生成函式,而且限制僅限於可微。輸入資料z可以從任意的分佈中取樣,G的輸入也無需與深度網路的第一層輸入一致(例如,可以將輸入z分為兩部分:z1和z2,分別作為第一層和最後一層的輸入,如果z2服從高斯分佈,那麼(x | z1)服從條件高斯分佈)。但z的維數要至少與x的維數一致,才能保證z撐滿整個x樣本空間。G的網路模型也不受任何限制,可以採用多層感知機、卷積網路、自編碼器等。因此,GAN對生成器的限制很少。
判別器D的輸入為G的輸出(G(z),0)和真實樣本(x,1)——其中,0表示fake,1表示real。判別器網路可以採用任意的二元分類器,訓練過程為典型的監督式學習。輸出為一個標量值,表示偽造的輸入G(z)為真實樣本的概率,當達到0.5時,說明判別器無法區分真實樣本和偽造樣本,即極小極大博弈達到了納什均衡,或者訓練過程已收斂。那麼生成器就是我們需要的生成模型,給定先驗分佈,輸出“真實”的樣本。
三、GAN相對於其他生成模型相比有什麼優勢
1. 相對於FVBN生成時間與x的維度成正比,GAN可以一次性生成樣本
2. 相對於BNs只有很少的概率分佈可以使用馬爾科夫鏈計算,非線性獨立成分分析要求隱變數與x有相同的維數,GAN對生成函式只有很少的限制
3. GAN框架中不需要變分約束,可用的具體模型族已經被稱為通用近似,所以GAN已經被認為是漸近一致的。一些VAE被推測為漸近一致,但這還沒有被證明。兩者最大的不同是,如果採用標準BP演算法,VAE不能採用離散變數作為生成器的輸入,而GAN的生成器不能產生離散變數的輸出。
4. 實際應用中,GAN相對於其他模型生成了質量更高的影象
四、GAN基本模型(引用GoodFellow 2014-06)
生成對抗網路是一種框架,通過對抗過程,通過訓練生成器G和判別器D。兩者進行一個極小極大(minmax)的博弈,最終達到納什均衡,即判別器無法區分樣本是來自生成器偽造的樣本還是真實樣本。以往的深度生成模型需要馬爾科夫鏈或近似極大似然估計,產生很多難以計算的概率問題。為避免這些問題而提出了GAN框架,訓練過程採用成熟的BP演算法即可。
基本模型:
1) 生成器G:輸入“噪聲”z(z服從一個人為選取的先驗概率分佈,如均勻分佈、高斯分佈等)。採用多層感知機的網路結構,用MLP的引數來表示可導對映G(z:),將輸入空間對映到樣本空間。G為可微函式。
2) 判別器D:輸入為真實樣本x和偽造樣本D(z),並分別帶有標籤real和fake。判別器網路可以用帶有引數多層感知機表示D(x;)。輸出為D(x),表示來自真實樣本資料的概率。
優化目標:
生成器G和判別器D在極小極大博弈(非凸優化)中扮演了兩個競爭對手的角色,用下列值函式V(G,D)來表示:
優化過程:
1) 訓練初期,當G的生成效果很差時,D會以高置信度來拒絕生成樣本,因為它們與訓練資料明顯不同。因此,log(1−D(G(z)))飽和(即為常數,梯度為0)。因此我們選擇最大化logD(G(z))而不是最小化log(1−D(G(z)))來訓練G。
2) 在訓練的內部迴圈中完成優化D是計算上不可行的,並且有限的資料集將導致過擬合。作為替代方法,我們在優化D的k個步驟和優化G的一個步驟之間交替更新。只要G變化足夠慢,可以保證D保持在其最佳解附近。
3) 當pg=pdata時,到達全域性最優(鞍點)
4) 當D達到區域性最優時,優化G近似的等價於最小化JS散度
5) pg最終收斂到pdata
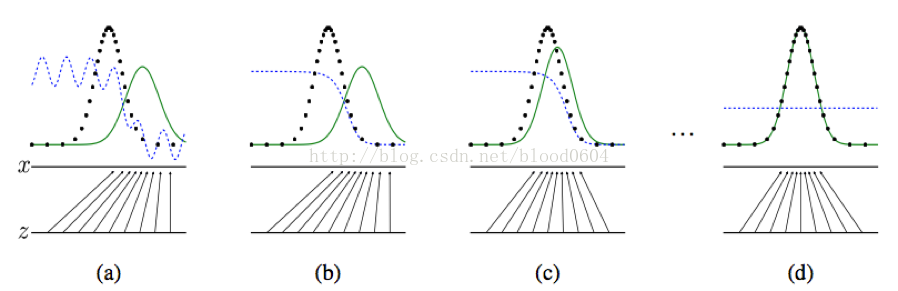
一維情況舉例:
z為從均勻分佈中取樣的噪聲,x為生成的樣本,z-x為生成器G的對映G(z)。圓點虛線為真實樣本所服從的正態分佈,實線為生成器所學習到的分佈,點畫線為分類邊界(即判別器對真實和偽造樣本分類的概率)。從(a)到(d)噪聲服從的均勻分佈逐漸對映為正態分佈,並隨著兩個分佈之間的“距離”——JS散度的不斷減小,最終學習到真實樣本的分佈,從而判別器無法區分真實樣本和偽造樣本。當訓練完成後,生成器會學習到將均勻分佈對映為正態的的對映函式。整個過程沒有用到標籤資訊,因而是無監督的學習。
五、改進的GANs(以時間為順序)
1. CGAN(Conditional GenerativeAdversarial Net 2014-11)
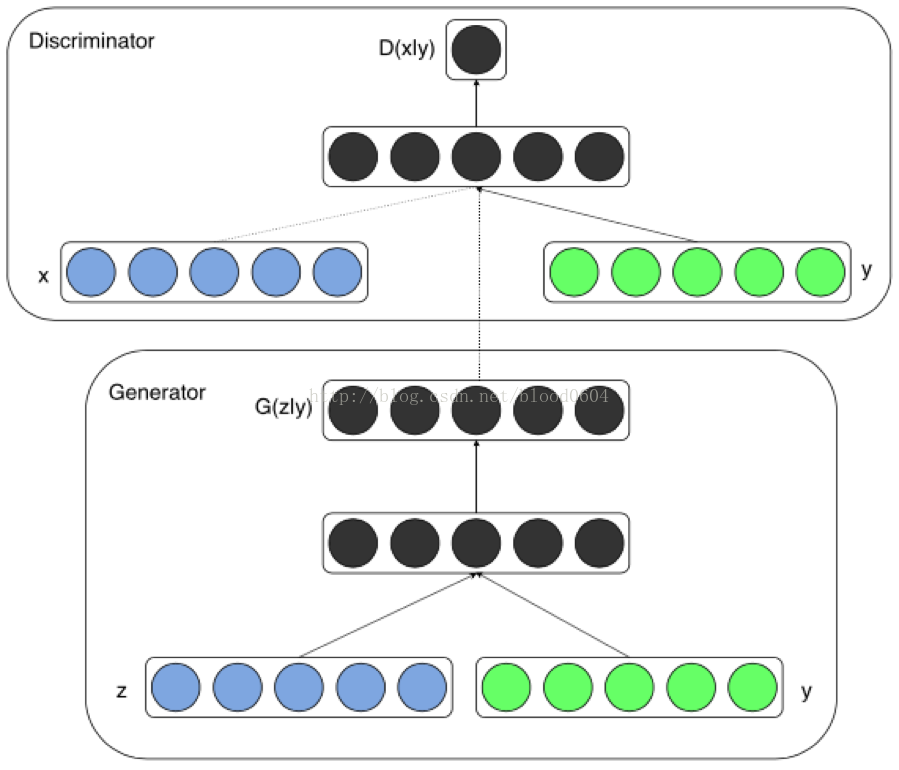
在無條件生成模型中,對生成資料的模型是沒有任何限制的。CGAN可以通過新增額外的資訊y來指導資料生成的過程。將y作為一個額外的輸入層,輸入生成器D和判別器G。比如,y可以是one-hot編碼的類標籤。
2. LAPGAN(Deep Generative Image Modelsusing a Laplacian Pyramid of Adversarial Networks 2015-06)
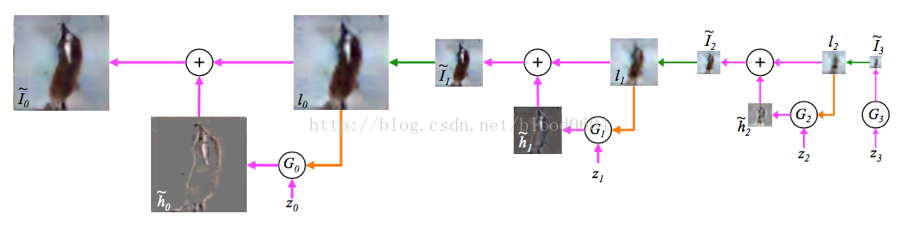
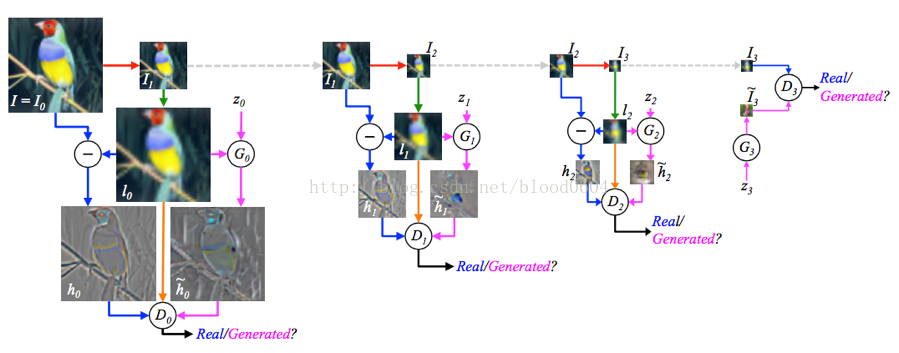
LAPGAN利用了CGAN,將影象作為條件同時作為判別器和生成器的輸入部分,同時採用拉普拉斯金字塔模型,不再一次性生成整個圖片,而是逐層生成整張圖片的每一部分。金字塔的每一層都採用GAN模型,並輸出一個樣本為真的概率值。實際上每一層都學習影象的L2損失,將影象先經過下采樣(即將圖片縮小為原來的1/2的尺寸,例如直接去掉偶數的行和列的畫素點),再經過上取樣(即將圖片擴大為原來的2倍,例如用奇數的行和列的畫素點填充偶數行列),作為條件分別輸入生成器、與真實影象相減輸入判別器、直接輸入判別器,從而每一層學習的是殘差損失。
取樣過程
訓練過程
3. CatGAN(Unsupervised and Semi-supervised Learning withCategorical Generative Adversarial Networks 2015-11)
CatGAN的主要目的是採用GAN進行半監督或無監督聚類問題。通常聚類問題分為兩類:1)生成式聚類方法,明確的對樣本分佈p(x)進行建模,如高斯混合模型、k-means、密度估計演算法;2)判別式的聚類方法,沒有明確對樣本分佈p(x)進行建模,直接通過一些分類機制,將無標籤的樣本劃分到某個類別下,如最大邊界聚類(MMC)、正則資訊最大化等。
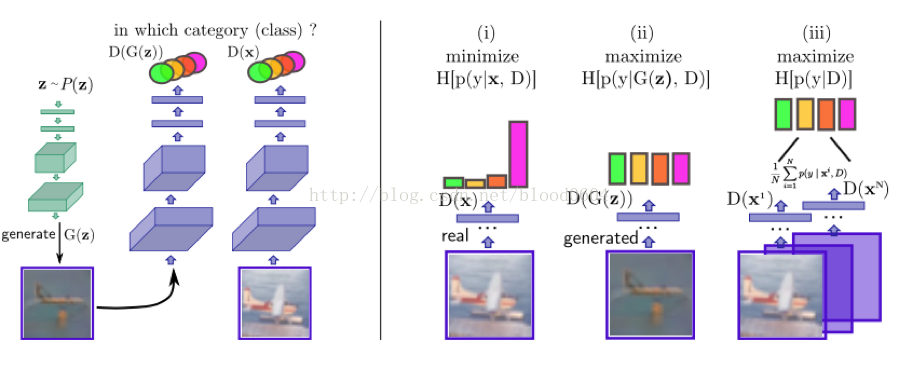
CatGAN試圖將以上兩種方法混合,判別器使用者最大化輸入樣本與標籤的互資訊,而生成器試圖用虛假的輸入樣本騙過判別器。
判別器:1)應該確定來自真實樣本的類別;2)不確定來自生成器的樣本分類;3)均等的使用所有的類別(假設噪聲是取樣與均勻分佈)
生成器:1)生成高度確定類別的樣本;2)在所有K個類別中平均分配樣本
目標函式:
4. DCGAN(Deep Convolutional GenerativeAdversarial Net 2015-11)
DCGAN採用的卷積或類逆卷積架構,實際上已經成為GAN的標準架構,在之後的幾乎所有改進中,都採用的是這種卷積架構。
1) 論文貢獻:
· 為CNN的網路拓撲結構設定了一系列的限制來使得它可以穩定的訓練。
· 使用得到的特徵表示來進行影象分類,得到比較好的效果來驗證生成的影象特徵表示的表達能力
· 對GAN學習到的filter進行了定性的分析。
· 展示了生成的特徵表示的向量計算特性。
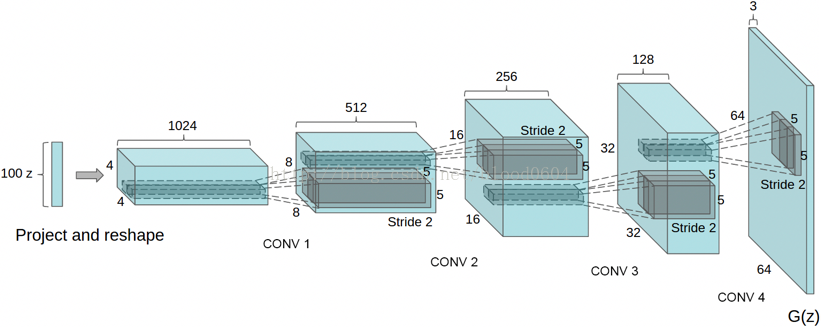
2) 模型結構
· 將池化層用卷積層替代,其中,在判別器上用帶步長的卷積替代,在生成器上用小步幅卷積替代。
· 在生成器和判別器上都使用批量歸一化
o 解決初始化差的問題
o 幫助梯度傳播到每一層
o 防止生成器把所有的樣本都收斂到同一個點。
o 直接將批量歸一化應用到所有層會導致樣本震盪和模型不穩定,通過在生成器輸出層和判別器輸入層不採用BN可以防止這種現象。
· 移除全連線層
o 全域性池化增加了模型的穩定性,但降低了收斂速度。
· 在生成器的除了輸出層外的所有層使用ReLU,輸出層採用tanh。
· 在判別器的所有層上使用LeakyReLU。
生成器網路
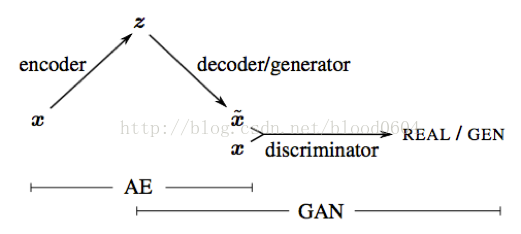
5. VAE-GAN(Autoencoding beyond pixels using a learned similaritymetric 2015-12)
VAE-GAN仍然是以生成高質量圖片為目的。將生成器用VAE(變分自編碼器)的解碼器代替,判別器用來度量樣本的相似性。利用判別器學好的表徵作為VAE重建目標的基礎,以更好度量資料空間的相似性。並用特徵級別的損失來代替元素級別的損失(如畫素的L2損失)以更好的學習資料分佈。p(z)為從標準正態分佈取樣的輸入噪聲,當訓練結束,VAE的解碼部分將噪聲對映為真實圖片。VAE-GAN充分利用了深度神經網路可以學習到高階表徵的特點,可以視為學習到的影象內容,可以視為學習到的影象風格。
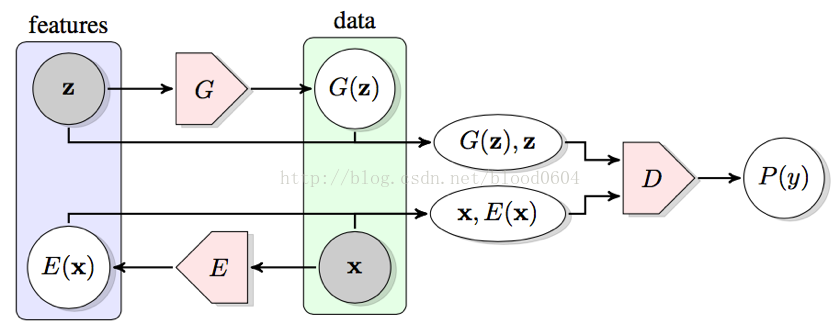
6. BiGAN(Adversarialfeature learning 2016-05)
BiGAN採用雙向GAN學習逆對映——將資料投影到潛在空間中,所得到的學習特徵表示對於輔助監督的辨別任務是有用的。生成器G將噪聲對映為偽造的樣本,而編碼器E將真實樣本對映到隱變數空間。編碼器E和生成器G必須學會相互反轉以騙過判別器D。BiGAN能夠在給定樣本x的情況下學習特徵z,那麼訓練好的編碼器E就能作為一個有用的特徵表示用於相關語義特徵的任務。同樣,當給定影象時,用於預測語義“標籤”的完全無監督學習的視覺模型,可以作為強大特徵表徵用於相關的視覺任務。隱藏特徵空間中的z就可以作為樣本在隱藏空間中的“標籤”。
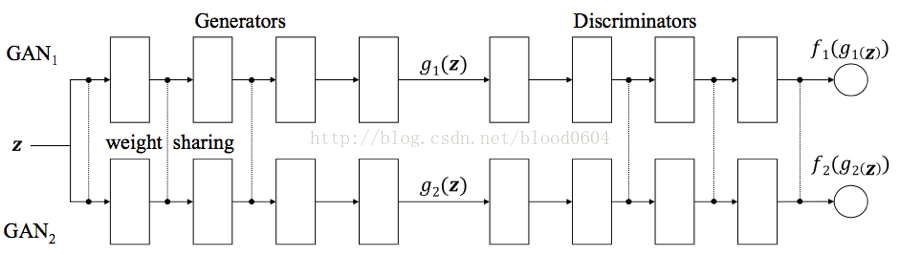
7. CoGAN(CoupledGenerative Adversarial Networks
CoGAN是為了學習多域影象的聯合概率分佈,例如影象的顏色和深度的聯合分佈。
該網路包括一對GAN:GAN1、GAN2。每個GAN都有一個生成器用來在一個域中合成影象,判別器用來分辨影象真假。通過對網路增加權值共享的限制——兩個生成器的前幾層共享權值(負責解碼高階語義特徵),兩個判別器的最後幾層(負責編碼高階語義特徵)。訓練好的CoGAN可以用來合成一對相似的影象——共享相同高階抽象但具有不同低階實現的影象對。
8. InfoGAN(InterpretableRepresentation Learning by Information Maximizing Generative Adversarial Nets2016-06)
通過互資訊(I(x;y) = H(x) - H(x | y))最大化的GAN解釋表徵學習。原始的GAN模型生成器以一種高度糾纏的方式使用噪聲輸入,噪聲的每個單獨的維度與生成的資料沒有語義關係。比如z中的哪些維度對應於光照變化或哪些維度對應於pose變化是不明確的。而infoGAN不僅能對這些對應關係建模,同時可以通過控制相應維度的變數來達到相應的變化,比如光照的變化或pose的變化。
噪聲輸入分為兩部分:1)不可壓縮的噪聲源z;2)針對資料語義特徵的隱變數噪聲c。那麼生成器的輸入就變為了G(z,c)。帶有互資訊正則化的目標函式變為:
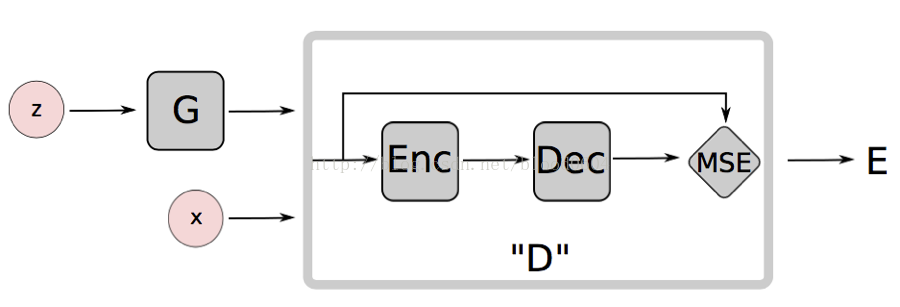
9. EBGAN(Energy-based GenerativeAdversarial Network 2016-09)
基於能量的生成對抗網路,將判別器視為一個能量函式,在真實資料的流形附近具有較低的能量值,其它區域則有較高的能量值。基於能量的模型本質上,是構建一個函式,將輸入空間中的每一個點對映為一個標量值——即“能量”。生成器作為一個引數函式,生成的樣本儘量被分配給低的能量值。判別器採用自編碼器,並將重構誤差作為能量值。
[·]+為max(0,·)函式
判別器:
生成器:
10. WGAN(WassersteinGAN 2017-01)
WGAN引入了一種新的度量分佈之間的“距離”——Wasserstein 距離,又叫地動距離或EM距離,從理論上基本解決了GAN訓練不穩定的問題。同時也指出梯度消失問題是由於原損失函式中log函式導致的。由於之前的GAN沒有衡量影象質量的方法,WGAN的損失同時可以評價影象的質量。該論文對GAN的理論改進具有極其重要的意義。
WGAN的提出分為兩篇論文,在該論文之前的一篇論文——《TOWARDS PRINCIPLED METHODS FOR TRAINING GENERATIVEADVERSARIAL NETWORKS》——從理論上徹底分析了GAN訓練存在的不穩定問題,並提出了一種臨時方案,即在真假樣本進入判別器前,對偽造樣本新增少量的噪聲。
在此之前的GAN模型都採用JS散度來衡量兩個分佈——真實樣本的分佈、偽造樣本的分佈——之間的“距離”,但JS散度或KL散度在兩個分佈沒有交集的情況下是沒有定義的,也就是無窮值。然而,樣本的分佈都處於高維空間的低維流形上,大多數情況下,兩個流形以1的概率具有零測度的交集——如兩個二維空間的一維流形,即平面中的兩條曲線,平面中的兩條任意曲線,僅有有限個交點,相對於無限長的曲線其長度可忽略,即測度為零。也就是原文中所描述的——模型的流形和真實分佈的流形不太可能有不可忽略的支撐集,也就意味著KL散度是沒有定義的,因此,用JS/KL散度來衡量兩個分佈之間的“距離”是不合適的。那麼,增加噪聲可以使兩個分佈之間具有交集,這也是機器學習中生成模型都具有噪聲項的原因。最典型的做法是新增較大寬度的高斯噪聲,但卻使生成的影象變得模糊。同時,一般情況下,影象的畫素值要被歸一化的(0,1)範圍內,在這種情況中,增加N(0,1)高斯噪聲產生的影響會遠遠大於影象本身的影響。
基於對不同的距離度量之間的比較,該論文提出採用EM距離來衡量不同分佈之間的“距離”。
W距離或EM距離:
是聯合分佈集合中的一個元素,其中的邊緣分佈為。
由於EM距離無法直接計算下确界(inf),因此需要根據Kantorovich-Rubinstein對偶問題求解。
為1階Lipschitz連續的條件,即函式f在整個定義域上,一階導數的絕對值小於等於1。而f函式可以用帶有引數的神經網路來表示,由於BP演算法要求一階偏導不為無窮,可以將限制條件放寬為:f函式滿足K階Lipschitz條件。在實際操作中,可以對神經網路的引數w進行裁剪,即限制在[-c,c]範圍內。因此判別器的優化問題轉化為最大化兩個分佈之間的EM距離,即:
其中,為帶有引數w的判別器網路,為帶有引數的生成器網路。判別器要最大化引數w以最大化EM距離。對引數w的裁剪是為滿足Lipschitz條件而強加的限制,而如果裁剪的範圍過大,判別器很難訓練達到最優;如果裁剪的範圍過小,那麼很容易導致梯度消失。
11. BEGAN(Boundary EquilibriumGenerative Adversarial Networks)
結合WGAN,提出了一種新的均衡方法,用於訓練自編碼器。這種方法使用者平衡生成器和判別器,並且提供了一種新的近似度量收斂的方法,訓練更加快速、穩定,影象質量更高。同時,還可以平衡生成影象的多樣性和影象質量。
本文的貢獻:
1) 簡單魯棒性很好的架構,標準的訓練方法,快速穩定的收斂
2) 一種平衡的概念——用於平衡生成器和判別器的能力
3) 一種新的方式——平衡影象的多樣性和影象質量
4) 近似的度量收斂,全域性損失在一定程度上能夠衡量影象質量
DCGAN利用卷積神經網路首先提高了影象質量。EBGAN將判別器視為一種能量函式。這個變體收斂穩定、容易訓練,並且對超引數具有很好的魯棒性。EBGAN同樣將其鑑別器實現為具有每畫素誤差的自動編碼器。WGAN提出了Wasserstein距離作為損失函式,同時也可以衡量收斂性,雖然收斂性很好、訓練穩定,但是訓練緩慢。
BEGAN用自編碼器作為判別器。典型的GAN直接匹配資料分佈,而BEGAN用W距離匯出的損失來匹配自編碼器的損失分佈。
首先,影象經過自編碼器的L1損失近似於正態分佈。基於這個假設,BEGAN模型用W距離衡量兩個正態分佈之間的距離。判別器D最大化兩個分佈的距離,而生成器G最小化兩個分佈之間的距離。
其次,判別器採用卷積網路構成的自編碼器,並移除池化層。生成器G採用與自編碼器中的解碼器相同的結構。影象經過自編碼器的損失採用L1範數作為損失:
該損失為一個標量值,經過自編碼器的多次迭代的損失值,服從正態分佈。
兩個一維正態分佈之間的W距離的平方為:
m1、m2為兩個分佈的均值,c1、c2為兩個分佈的方差。
上述方程的解為:
即將真實圖片重構的損失均值為零,而將生成器重構圖片的損失儘量大。而生成器儘量減小兩個損失之間的距離,從而使判別器無法區分。
損失函式分別為:
LD即為兩個損失之間的負W距離。判別器最大化兩個分佈之間的距離,即為最小化兩個分佈之間的負距離。生成器最小化損失,讓生成的影象儘量的重構為真實的影象。
最後,又引入一個超引數γ=L(G(z))/L(x),作為平衡多樣性和影象清晰度的比例係數。同時,加入一個可調節的係數kt,用負反饋系統調節生成器和判別器之間的能力。由於,開始訓練時,真實影象經過自編碼器的損失較大,判別器很容易區分真實影象和生成的影象。初始時,kt=0,最小化LD相當於讓判別器專注於自編碼任務。同時,由於剛開始訓練時,真實影象經過自編碼器的值較大,,kt的值逐漸增大,LD中的比例逐漸增大。當真實影象重構的比較好時,判別器更多的關注拉近兩個分佈之間的距離,同時,kt逐漸減小,直到γL(x)-L(G(z))=0。
實驗中發現,BEGAN收斂比較緩慢。
六、GAN有哪些應用
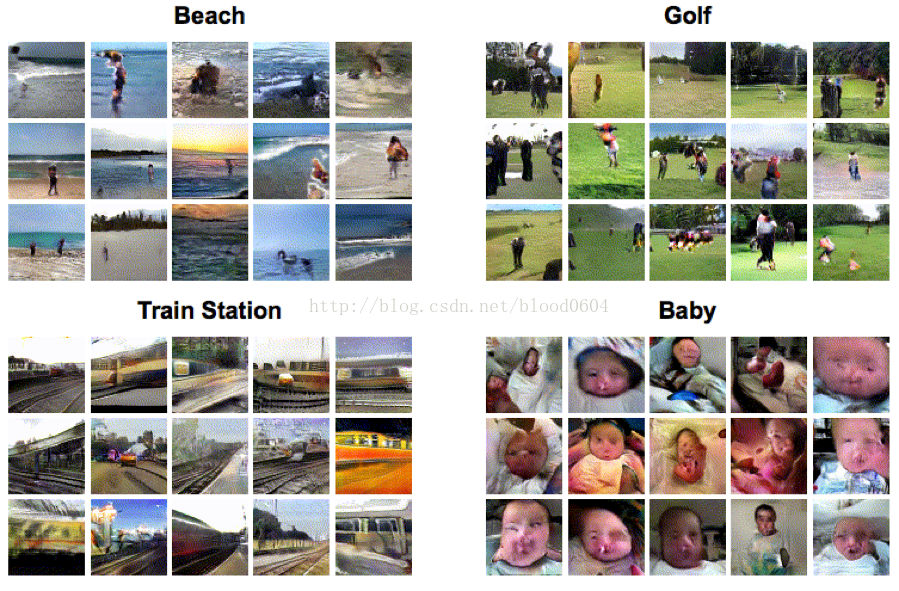
1. 影象生成
影象生成是生成模型的基本問題,GAN相對先前的生成模型能夠生成更高影象質量的影象。
2. 高解析度影象生成(PPGN、BEGAN、BEGAN等)
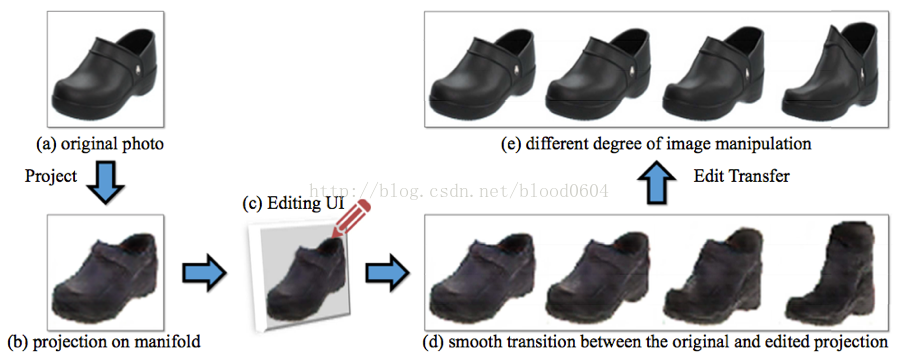
3. 互動式影象生成(iGANhttps://research.adobe.com/project/igan/)
4. 超解析度(SRGAN)——如將32*32的影象擴充套件為64*64的真實影象
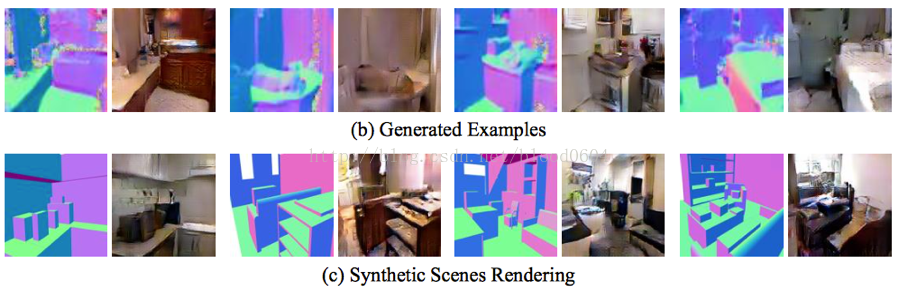
5. 合成場景渲染(S2GAN)
6. 影象修復(ContextEncoders: Feature Learning by Inpainting)
8. 根據文字生成影象(StackGAN)
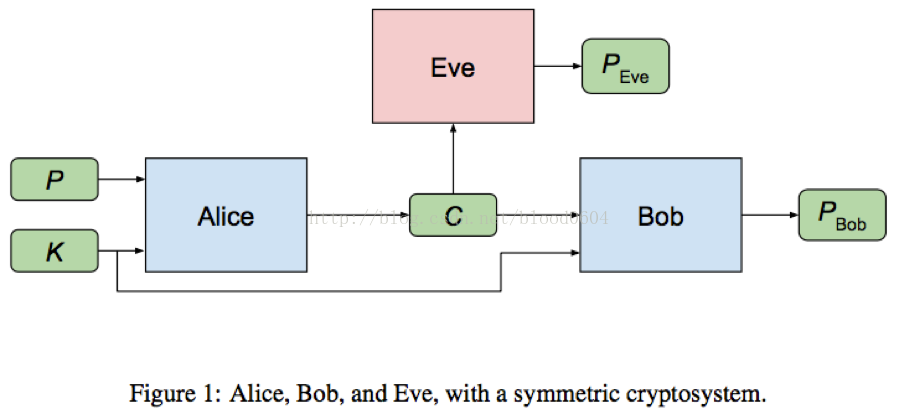
9. 通訊加密(Learningto protect communications with adversarial neural cryptography)
10. 2D-3D模型重建(3D-GAN)
11.資訊檢索(IRGAN——SIGIR2017的滿分論文