機器學習及python實現——樸素貝葉斯分類器
阿新 • • 發佈:2019-01-05
問題引入
考慮構建一個垃圾郵件分類器,通過給定的垃圾郵件和非垃圾郵件的資料集,通過機器學習構建一個預測一個新的郵件是否是垃圾郵件的分類器。郵件分類器是通常的文字分類器中的一種。
樸素貝葉斯方法
貝葉斯假設
假設當前我們已經擁有了一批標識有是垃圾郵件還是非垃圾郵件的資料集,然後我們來構建一個分類器。
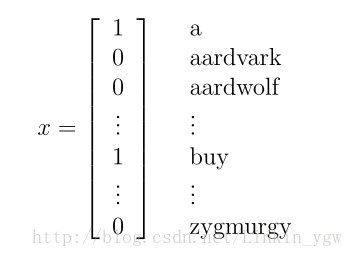
我們可以通過一個特徵向量來表示一封郵件,向量的維度就是字典中單詞的個數。如果字典中的第i個單詞包含在郵件中,那個這個向量的
表示郵件中存在單詞a,buy,而aardvark,aardwolf和zygmurgy不存在。從這裡可以看到,向量的維度為字典單詞的個數,這裡為50000。
有了特徵向量,我們來構建模型,實際上,我們需要構建的就是這樣一個條件概率模型
樸素貝葉斯方法
有了以上的樸素貝葉斯假設,那我們可以構建我們的模型
將模型引數化