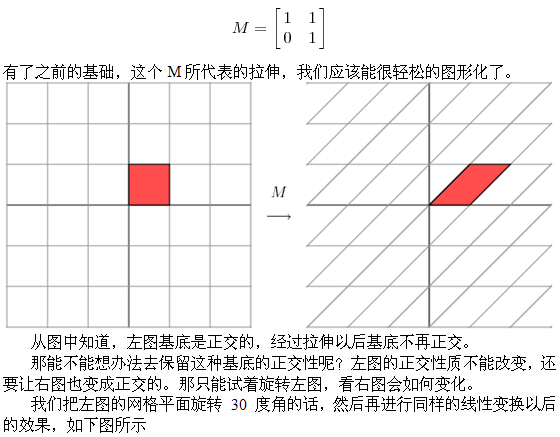
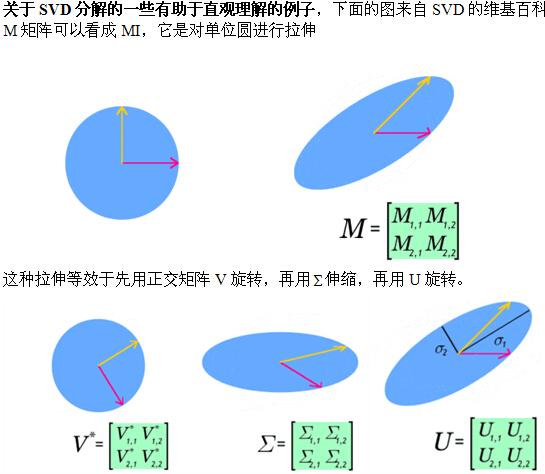
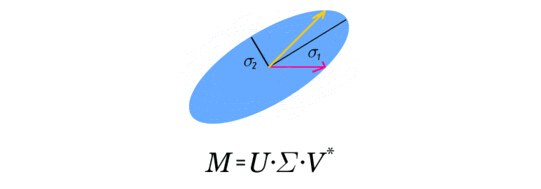
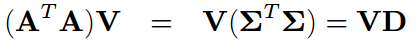SVD 與 PCA 的直觀解釋(3): SVD的直觀解釋及推導
阿新 • • 發佈:2019-01-05
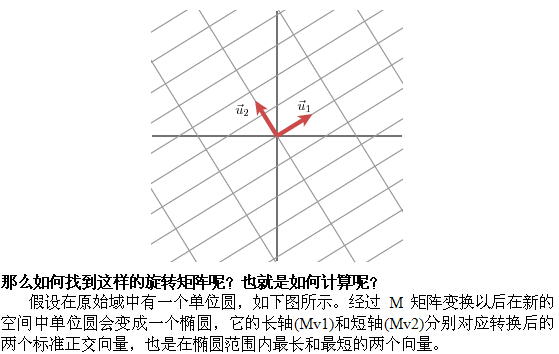
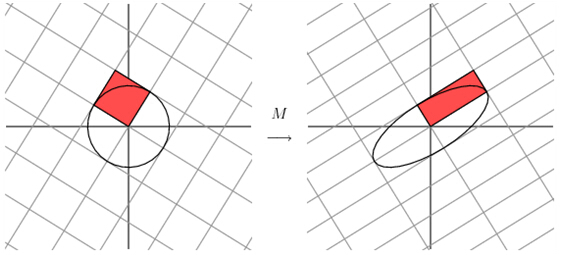
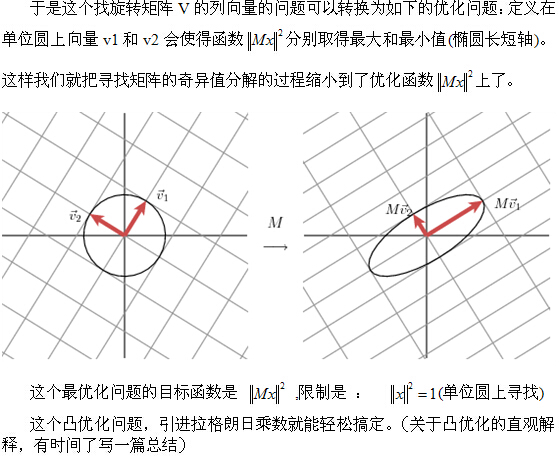
引子:SVD分解就是把一個實數矩陣M分拆成UDV。U,V都是正交旋轉矩陣。這個分拆可以形象的理解為,我要看看這個空間M性質怎麼樣?那我可以用標準笛卡爾空間來構造出一個一模一樣的M空間。想象M空間是個特殊形狀的泥塑,笛卡爾空間是塊標準的正方形泥塊。把笛卡爾空間放在手裡,先旋轉著看看(即左乘V),再找合適的地方捏捏它(再左乘D),好讓它和M一樣。最後再旋轉(再左乘U),把它擺得和M一樣。這樣就360度無死角的構造了一個M空間。如果發現M空間有的地方很扁,那麼我就掉丟這個維度,這就是SVD的降維,也是SVD的核心。
註釋:關於上面為何是特徵向量的說明。
PS:一室友秦屌,問我M不是方陣,是3*2的矩陣。作用在2*1的向量 x 上,Mx 就變成了三維的了。這還能通過兩次旋轉達到效果嗎?
reference: