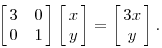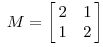一直想弄明白SVD分解後面蘊含的直觀意義，可這牽扯到矩陣乘法和線性變換的物理含義的理解。在考慮SVD用途時又牽扯到PCA降維，而PCA降維裡又扯到特徵值和特徵向量。於是，索性全記下來，供諸位探討學習。

全文將解答如下問題：

   經常看到在一個向量的左側乘以一個矩陣，那矩陣乘法到底有什麼樣的含義？直觀的解釋又是什麼？文章將從拉伸和基變換兩個方面做解釋。請重視對線性變換的理解，它對理解特徵向量，SVD有很大好處。

二.特徵值和特徵向量

在我們的直觀世界中特徵值和特徵向量到底是一種怎樣的存在？

為什麼要進行SVD分解？他有什麼直觀的物理或者幾何含義？

SVD分解的公式又是如何推匯出來的？

四.PCA降維

資料降維是幹嘛？為什麼能丟掉一些維度，為什麼特徵值大就是主成分？SVD分解在降維中的應用。

一.線性變換

      什麼是線性變換？在數學中，線性對映（也叫做線性變換或線性運算元）是在兩個向量空間之間的函式，它保持向量加法和標量乘法的運算。術語“線性變換”特別常用，尤其是對從向量空間到自身的線性對映。

      如果 V 和 W 是有限維的，並且在這些空間中有選擇好的基，則從 V 到 W 的所有線性對映可以被表示為矩陣；（來自維基百科）

      上面說的這麼迷糊，線性變換就是向量加法和標量乘法的運算，而矩陣乘法正好就只有加和乘的運算。

      所以這裡，我要解釋的是線性變換在這種加法和乘法裡所帶來的拉伸效果或者說是解釋向量如何在不同矩陣空間中表示。

       這部分首先用兩個特例來演示線性變換的拉伸效果（其實也就是一個矩陣左乘一個向量），然後用基底的變換來解釋矩陣乘法，以及為什麼會產生這種效果。

     先通過兩個二維的簡單特例來圖示線性變換的拉伸效果：

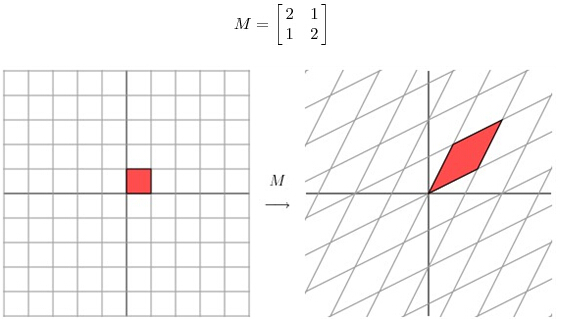
1.假設有一個對角矩陣M，M乘以一個向量(x,y)可以看做M將點(x,y)變換為另一個點

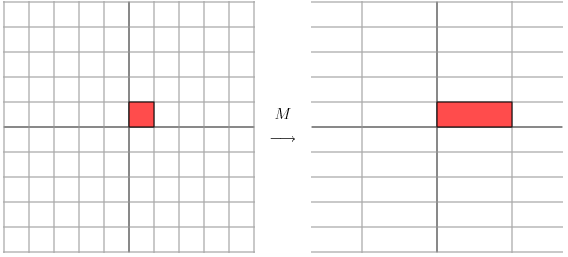
變換的效果如下，變換後的平面僅僅是沿 X 水平方面進行了拉伸3倍，垂直方向是並沒有發生變化。

   2.看另一個矩陣

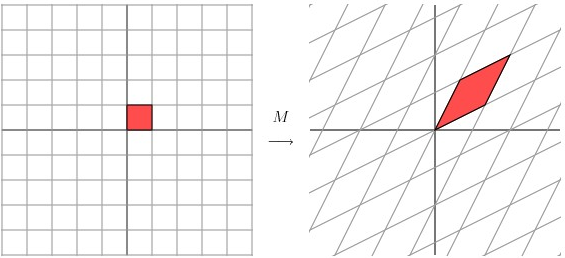
用這個矩陣乘以其他向量，產生的效果：

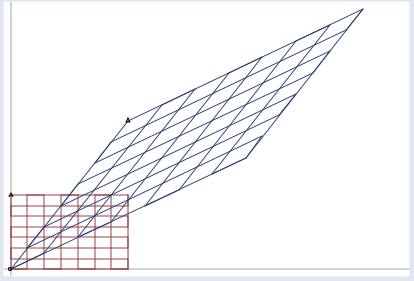
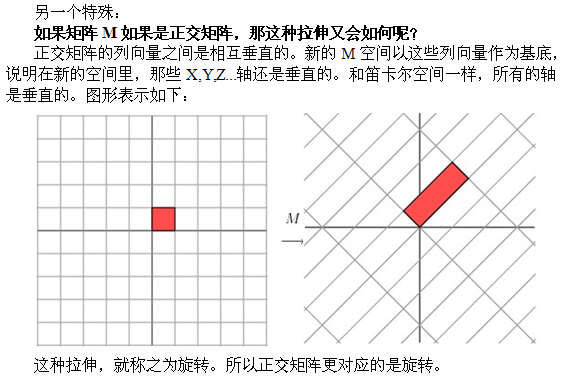
這種效果的另一種演示，請注意基底的變化(即圖中矩陣的邊界，原來是正交的，變化後不是)：

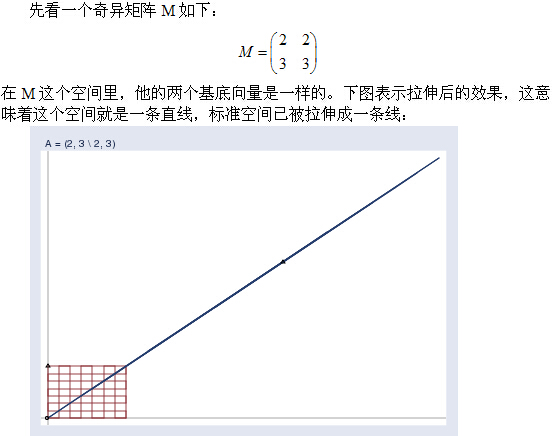
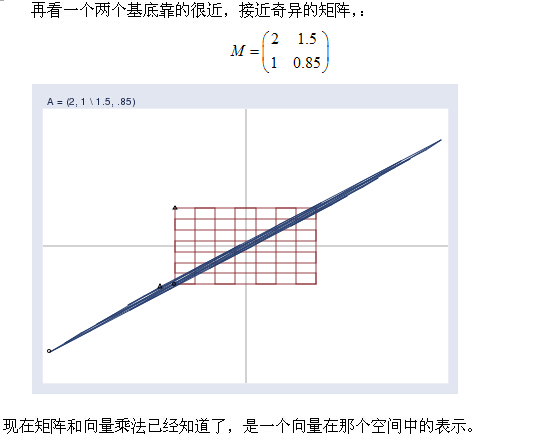
      在進行下面的解釋之前，我想灌輸一個概念，一個矩陣的列向量就是一組“基底"(先不談奇異矩陣)。這些基底就張成了一個空間。如3階單位矩陣I，它的列向量就張成了我們熟知的三維座標系笛卡爾空間。