機器學習方法篇(18)------聚類
● 每週一言
是學是玩,和時間賽跑。
導語
在實際生活中,無論是超市貨架還是網路社交群體,都體現著歸類的相似性,即所謂的“物以類聚,人以群分”。在機器學習中,專門有這麼一類針對類別劃分的演算法,就是接下來要講的聚類。那麼,聚類的數學含義是什麼?又有哪些常用演算法?
聚類
所謂無監督學習,就是通過學習不帶類別標籤的樣本,得到樣本之間內在的規律和聯絡。而聚類則是無監督學習最常用,也是應用最為廣泛的一種實現手段。
顧名思義,聚類就是把相似的樣本歸為一類。那麼,如何度量樣本之間的這種相似性?
我們知道,樣本由特徵組成,而特徵又分為連續(有序)特徵和離散(無序)特徵兩種。因此,樣本相似性度量,其實就是樣本特徵之間的相似性度量。
對於連續特徵的相似性度量,最常用的是閔可夫斯基距離,公式如下:
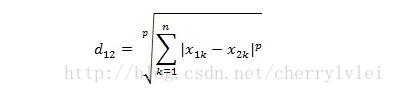
其中k表示特徵序號,而p值不同距離含義不同:p = 1計算的是曼哈頓距離,p = 2就是我們最熟悉的歐氏距離,p → ∞時計算的則是切比雪夫距離。
不過,閔可夫斯基距離有兩個明顯的缺點:一是特徵之間的量綱(單位)被等同對待,這通常是不合理的;二是未考慮特徵值本身的分佈規律,如遇到類似長尾分佈,這種距離度量的效果往往大打折扣。第一點可以採用特徵加權應對,第二點則可以採用特徵值標準化或者分箱來應對。
除開閔可夫斯基距離,常見的連續特徵相似性度量方法還有馬氏距離、夾角餘弦、Pearson相關係數等。

對於離散特徵的相似性度量
此外,離散特徵的相似性度量還可以採用VDM(Value Difference Metric)值差分度量法。不過VDM的前提必須是帶類別標籤的聚類,其演算法原理是通過考慮不同離散屬性值在相同類別標籤下佔比的關係,得出離散屬性值之間的相似度。
以上提到的相似性度量都屬於距離度量,而距離度量需要滿足以下四個基本性質:
非負性: d(a, b) ≥ 0;
同一性: d(a, b) = 0,當且僅當a = b;
對稱性: d(a, b) = d(b, a);
直遞性:

然而並不是所有的相似性度量一定要滿足以上四個性質,尤其是直遞性。比如“人馬”、“人”和“馬”,“人馬”分別與“人”和“馬”相近,但是“人”和“馬”卻截然不同。
再比如,我的朋友之間並不一定是朋友,同樣也不滿足直遞性。這涉及到了知識圖譜中實體和關係的概念,在這裡不多講,有興趣的讀者可自行刨根問底。
這裡順便提一下軟聚類。常規的聚類結果,樣本最終只會歸為某一類別,而軟聚類則允許樣本最終歸為多個類別。
聚類的演算法實現有很多,大體可以分為劃分聚類法、層次聚類法、密度聚類法以及模型聚類法四種。接下來的幾周,我將挑選幾個常用的聚類演算法深入講解,敬請期待。
結語
感謝各位的耐心閱讀,後續文章於每週日奉上,敬請期待。歡迎大家關注小鬥公眾號 對半獨白!

