基於損失函式的標準

混淆矩陣

混淆矩陣用在分類器中，是對每一類樣本的統計，包括正確分類和錯誤分類的個數。對於m類樣本，可能的錯誤種類有$m^2-m$個。
對於2分類問題存在4種可能的情況：

實際的類
預測的類	c_+	c_-
	c_+	TurePositive	FalseNegative
	c_-	FalsePositive	TureNegative
	總計	TurePositive+FalsePositive	FalseNegative+TureNegative

多分類問題類似，只是情況更多。

準確率及誤差率的度量

為了度量預測的精確度，隱含假設每一個錯誤分類的樣本成本相同，引入誤差率和準確率兩個指標作為這種成本的度量。
誤差率： 錯誤分類的樣本數(E)與檢測樣本總數(S)的比值
$R=E/S$
準確率： 正確分類的樣本數與檢測樣本總數(S)的比值
$A=1-R=\frac{S-E}{S}$

我們也可以引入更全面的指標：
用$pos$表示真實正例的樣本數，$neg$表示真實負例的樣本數，$t_{-pos}$表示正確預測的正例樣本數，$f_{-pos}$表示負例被當成正例的樣本數，$t_{-neg}$表示正確預測的負例樣本數，$f_{-neg}$表示正例被當成負例的樣本數。以下括號中的文字有些是自己給取的名字，不要跟其他地方混淆了。
靈敏度(真正率)： $Sensitivity=\frac{t_-pos}{pos}$，即正例中被準確預測的比例（有點查全的感覺，真的有這麼多正例，有多少被挑出來了）
即召回率(查全率R)： 計算方法同靈敏度，相同東西在不同場合下的叫法。
特異性（真負率）： $Specificity=\frac{t_-neg}{neg}$，即負債中被準確預測的比例（有點查全的感覺，真的有這麼多負例，有多少被挑出來了）
精度（正例檢出率）： $Precision=\frac{t_-pos}{t_-pos+f_-pos}$，即在預測結果的正例裡真實正例的比例（有點查準的感覺，預測了這麼多，多少預測對了）
即準確率(查準率P)： 與精度計算方法相同
錯誤正例(假正率)： $False Positive Rate=1-\frac{t_-neg}{neg}$，即正例被當成負例的樣本數佔預測結果的負例樣本數的比例
錯誤負例(假負率)： $False Negetive Rate=1-\frac{t_-pos}{pos}$，即負例被錯誤當成正例的樣本數佔預測結果的正例樣本數的比例
最終
準確率: $A=\frac{t_-pos+t_-neg}{pos+neg}=\frac{t_-pos}{pos}*\frac{pos}{pos+neg}+\frac{t_-neg}{neg}\frac{neg}{pos+neg}$
F_1值： $F_1=\frac{2*P*R}{P+R}$，更一般的形式為$F_1=\frac{(1+\beta^2)P*R}{(\beta^2*P)+R}$這裡的P指查準率，R指查全率
β=1退化為F1；β>1查全率有更大影響；β<1查準率有更大影響。
巨集平均（macro-average）: 一般用在文字分類器，是先對每一個類統計指標值，然後在對所有類求算術平均值。巨集平均指標相對微平均指標而言受小類別的影響更大。
微平均（micro-average）： 一般用在文字分類器，是對資料集中的每一個例項不分類別進行統計建立全域性混淆矩陣，然後計算相應指標。
平均準確率(Average Per-class Accuracy): 為了應對每個類別下樣本的個數不一樣的情況，計算每個類別下的準確率，然後再計算它們的平均值。
對數損失函式(Log-loss): 在分類輸出中，若輸出不再是0-1，而是實數值，即屬於每個類別的概率，那麼可以使用Log-loss對分類結果進行評價。這個輸出概率表示該記錄所屬的其對應的類別的置信度。比如如果樣本本屬於類別0，但是分類器則輸出其屬於類別1的概率為0.51，那麼這種情況認為分類器出錯了。該概率接近了分類器的分類的邊界概率0.5。Log-loss是一個軟的分類準確率度量方法，使用概率來表示其所屬的類別的置信度。對數損失函式越小，模型就越好。可參考：對數損失函式(Logarithmic Loss Function)的原理和 Python 實現

評價模型成本的視覺化工具

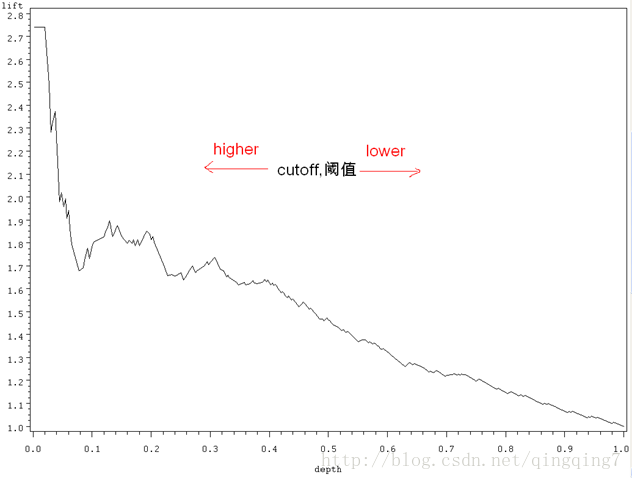
lift圖

lift 叫提升指數，也就是運用模型比不運用模型精度的提升倍數。
$lift=\frac{t_-pos}{t_-pos+f_-pos}/\frac{t_-pos+f_-neg}{t_-pos+f_-neg+f_-pos+t_-neg}$
也可以表示為
$lift=\frac{累計預測精度}{平均精度}$
結論是：提升指數越高，模型的準確率越高。
對準確率進行提升的例子：

假設根據以往的經驗，問卷調查的迴應率為20%，即發出100份問卷收回的有20份，但是通過對歷史資料的分析發現特定人群的迴應率會更高（資料分析的過程即為建模），然後對特定人群進行發放整個迴應率就得到提升。

用在資料探勘模型裡也是一樣，利用模型能對準確率提升越多，單方面來講模型效果就越好。
具體做法如下：
I、 計算出測試樣本中正例的百分比，即為平均精度；
II、 利用模型對測試樣本進行預測，按預測得分降序將樣本排序，將排序好的樣本分成10份，即按10分位數操作；
III、 計算第1份樣本中的預測精度，然後利用預測精度/平均精度，得到第1份資料的提升指數；
IV、 計算至第2份樣本處的累計預測精度，然後利用累計預測精度/平均精度，得到至第2份樣本處的提升指數；
VI、 依次得到10個節點處的提升指數；
VI、 畫出基線（各節點處均為1）及不同模型提升指數的曲線圖；
VII、 進行模型效果對比，圖形越高越好；

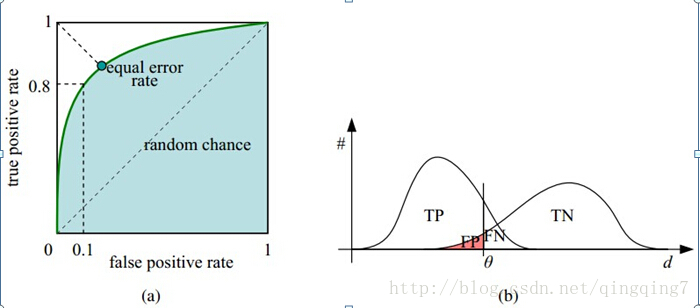
ROC曲線

ROC曲線是利用真正率為縱軸，假正率為橫軸畫出的曲線，用來評估模型預測準確率。很明顯，當真正率大越近1，假正率越接近0是模型越好。
對於給定的一組樣本，我們只能得到一個真正率和一個假正率（對應圖上的一個點），那如何畫ROC曲線呢？
通過設定不同的閾值，比如邏輯迴歸中可以設定概率>0.5的點為正例，在此閾值下可以得到ROC曲線上的一個點；更改閾值，如概率>0.6的點為正例，同樣可以得到ROC曲線上的一個點；不同的閾值可以得到一組點，即得到了ROC曲線；

真正率大越近1，假正率越接近0是模型越好，在圖上的表現就是ROC曲線越靠近(0,1)點，越遠離$45^o$對角線；
評價模型有很多指標，為什麼還要使用ROC和AUC呢？因為ROC曲線有個很好的特性：當測試集中的正負樣本的分佈變換的時候，ROC曲線能夠保持不變。在實際的資料集中經常會出現樣本類不平衡，即正負樣本比例差距較大，而且測試資料中的正負樣本也可能隨著時間變化。
ROC曲線在概念上和PR曲線類似,它是對分類器的真陽性率假陽性率的圖形化解釋。
真陽性率(TPR)是真陽性的樣本數除以真陽性和假陰性的樣本數之和。換句話說,TPR是 真陽性數目佔所有正樣本的比例。這和之前提到的召回率類似,通常也稱為敏感度。
假陽性率(FPR)是假陽性的樣本數除以假陽性和真陰性的樣本數之和。換句話說,FPR是 假陽性樣本數佔所有負樣本總數的比例。

AUC曲線

AUC(area under curve): 即ROC曲線下的面積。
若一個學習器的ROC曲線被另一個包住，後者的效能能優於前者；若交叉，判斷ROC曲線下的面積，即AUC。
關於AUC的計算方法，可參考AUC計算方法總結
在考查AUC時也要考查其他指標AUC越大，正確率就越高？

areaUnderPR

這裡的PR指查準率和查全率 .
通常,準確率和召回率是負相關的,高準確率常常對應低召回率,反之亦然。為了說明這點, 假定我們訓練了一個模型的預測輸出永遠是類別1。因為總是預測輸出類別1,所以模型預測結果 不會出現假陰性,這樣也不會錯過任何類別1的樣本。於是,得到模型的召回率是1.0。另一方面, 假陽性會非常高,意味著準確率非常低(這依賴各個類別在資料集中確切的分佈情況)。
準確率和召回率在單獨度量時用處不大,但是它們通常會被一起組成聚合或者平均度量(比如f1得分)。二 者同時也依賴於模型中選擇的閾值。
直覺上來講,當閾值低於某個程度,模型的預測結果永遠會是類別1。因此,模型的召回率 為1,但是準確率很可能很低。相反,當閾值足夠大,模型的預測結果永遠會是類別0。此時,模 型的召回率為0,但是因為模型不能預測任何真陽性的樣本,很可能會有很多的假陰性樣本。不 僅如此,因為這種情況下真陽性和假陽性為0,所以無法定義模型的準確率。
準確率-召回率(PR)曲線,表示給定模型隨著決策閾值的改變,準確率和召回 率的對應關係。PR曲線下的面積為平均準確率。直覺上,PR曲線下的面積為1等價於一個完美模 型,其準確率和召回率達到100%。
當正負樣本差距不大的情況下，ROC和PR的趨勢是差不多的，但是當負樣本很多的時候，兩者就截然不同了，ROC效果依然看似很好，但是PR上反映 效果一般。解釋起來也簡單，假設就1個正例，100個負例，那麼基本上TPR可能一直維持在100左右，然後突然降到0.
areaUnderPR和AUC更詳細的情況可檢視，ROC曲線和PR曲線。兩者的分子分母都不一樣

評估分類器的準確率

上面講的評價模型的指標或曲線都是在測試集中進行的，也就是我們需要將資料集分為訓練集和測試集，訓練集用於訓練模型引數，測試集用於檢驗模型在資料中的預測效果。這就是我們評估分類器大的方法。下面介紹將資料劃分為訓練集和測試集的方法。

再替換方法

所有的資料即用於訓練模型也用於檢驗模型

保持方法和隨機子抽樣

保持方法(hold out)： 按一定比例隨機地從資料集中抽取一部分樣本作訓練集，剩下的樣本為測試集，通訓練集在2/3~4/5之間；
隨機子抽樣(random subsampling)： 抽取一定比例樣本做為訓練集，剩下的樣本為測試集；然後在第1次的訓練集重複該操作；重複n次，評論指標的平均值作為最終的評價值；這是一種無放回抽樣；

交叉驗證法

K折交叉驗證(K-fold cross-validation): 將樣本分成K份，每份數量大致相等，然後用其他的某一份作為測試，其他樣本作為訓練集，得到一個模型和一組預測值及模型評估值；迴圈這個過程K次，得到K組模型評估值，對其取平均值即得到最終的評估結果；
留一(leave-one-out): 是K-fold cross-validation的特徵形式，每次只取一個樣本作為測試樣本，其餘樣本作為訓練樣本，重複該過程K次（假如樣本總數為K）。

自助法

自助法(bootstrap method): 在資料集中採用有放回的方式抽樣，產生訓練集和測試集；重複該過程n次。

基於統計檢驗的標準

統計模型之間的距離

距離是典型的相似性指標。
歐氏距離
熵距離
卡方距離
0-1距離
我並不認為用距離評估模型的效果是一種好的做法，只有不同類樣本在樣本內扎堆，類間分離的時候這種檢測才是一致的。

統計模型的離差

離差即誤差的統稱：如標準差，方差都為這一類
歐氏離差即為平均誤差和。

基於記分函式的標準

貝葉斯標準

計算標準

交叉檢驗標準

利用交叉檢驗的處理方法，再配合其他指標如離差進行檢驗。

自展標準

遺傳演算法

其他評價指標

計算速度： 分類器訓練和預測需要的時間；
魯棒性： 處理缺失值和異常值的能力；
可擴充套件性： 處理大資料集的能力；
可解釋性： 分類器的預測標準的可理解性，像決策樹產生的規則就是很容易理解的，而神經網路的一堆引數就不好理解，我們只好把它看成一個黑盒子。

迴歸模型評估指標

RMSE（root mean square error，平方根誤差）： 其又被稱為RMSD（root mean square deviation），RMSE對異常點（outliers）較敏感，如果迴歸器對某個點的迴歸值很不理性，那麼它的誤差則較大，從而會對RMSE的值有較大影響，即平均值是非魯棒的。其定義如下：
MAE（ mean absolute error，平均絕對誤差）：
Quantiles of Errors： 為了改進RMSE的缺點，提高評價指標的魯棒性，使用誤差的分位數來代替，如中位數來代替平均數。假設100個數，最大的數再怎麼改變，中位數也不會變，因此其對異常點具有魯棒性。
判定係數（coefficient of determination，記為$R^2$或$r^2$）: 用於度量因變數的變異中可由自變數解釋部分所佔的比例，以此來判斷統計模型的解釋力。

sklearn中的評價函式

分類主要是基於混淆矩陣，迴歸主要是基於誤差。

sklearn中 F1-micro 與 F1-macro區別和計算原理
區別是micro是對所有樣本求f1 score而macro是先在組內先求f1 scroe，然後對這些f1 scroe求加權平均；

y_true = [1, 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 4, 4]
y_pred = [1, 1, 1, 0, 0, 2, 2, 3, 3, 3, 4, 3, 4, 3]
print(f1_score(y_true,y_pred,labels=[1,2,3,4],average='micro'))
#>>> 0.615384615385

如果採用交叉驗證，可以如下設定,可以看到它對每一組測試樣本都會計算一個f1_score，我們可以簡單採用這些f1_score的平均值來綜合衡量模型的好壞，從而指導我們調參。

>> from sklearn import metrics
>>> scores = cross_val_score(
...     clf, iris.data, iris.target, cv=5, scoring='f1_macro')
>>> scores                                              
array([ 0.96...,  1.  ...,  0.96...,  0.96...,  1.        ])